Jan Łukasiewicz

Jan Łukasiewicz (Leópolis, 21 de diciembre de 1878 - Dublín, 13 de febrero de 1956) fue un matemático, lógico y filósofo polaco, figura de la Escuela de Leópolis-Varsovia y uno de los más importantes artífices del desarrollo de la lógica en Polonia. Introdujo la notación polaca y renovó el cálculo proposicional, colaborando con Alfred Tarski. Pionero de las lógicas polivalentes, pasó de su lógica trivalente para “futuros contingentes” a modelos con infinitos valores. Rector de la Universidad de Varsovia y Ministro de Educación (1919), formó discípulos clave para el desarrollo posterior de la lógica, tendiendo redes con Heinrich Scholz.

Jan Łukasiewicz
Información personal
Nacimiento	21 de diciembre de 1878 Leópolis (Imperio austrohúngaro)
Fallecimiento	13 de febrero de 1956 (77 años) Dublín (Irlanda)
Sepultura	Mount Jerome Cemetery y Cementerio Powązki
Nacionalidad	Austrohúngara e irlandesa
Lengua materna	Polaco
Educación
Educación	doctor en Filosofía
Educado en	Universidad de Leópolis Universidad de Varsovia
Supervisor doctoral	Kazimierz Twardowski
Alumno de	Kazimierz Twardowski
Información profesional
Ocupación	Matemático, filósofo, profesor universitario e informático teórico
Área	Lógica y matemáticas
Cargos ocupados	Ministro de Educación Nacional de Polonia (1919) Rector de la Universidad de Varsovia (1922-1923)
Empleador	Universidad de Varsovia Universidad de Leópolis
Estudiantes doctorales	Jerzy Słupecki
Estudiantes	Alfred Tarski
Partido político	Camp of National Unity
Distinciones	Comendador con Estrella de la Orden Polonia Restituta Comendador de la Orden Polonia Restituta (1923) Orden del Mérito de la República de Hungría (1935)

Jan Leopold Łukasiewicz nació el 21 de diciembre de 1878 en Leópolis (Ucrania), entonces capital de la Galicia austríaca dentro del Imperio austrohúngaro. Hijo único de Paweł Łukasiewicz, capitán del ejército austríaco, y de Leopoldine Holtzer, hija de un funcionario de gobierno austriaco, creció en un hogar polacohablante pese al entorno administrativo germano-austríaco. Su educación secundaria transcurrió en un Gimnazjum clásico de Leópolis, con fuerte formación en lenguas clásicas; estudios que concluyó en 1897. Ese mismo año inició la carrera de Derecho en la Universidad de Leópolis, pero en 1898 cambió a Matemáticas —bajo la tutela de Józef Puzyna— y Filosofía —con Kazimierz Twardowski, recién nombrado profesor extraordinario (1895)—, completando en 1902 el doctorado en Filosofía con su disertación “O indukcji jako inwersji dedukcji” (Sobre la inducción como la inversa de la deducción, en español) con mención sub auspiciis Imperatoris (recibiendo un anillo de diamantes otorgado por el emperador Francisco José I) por sus calificaciones sobresalientes.^[1]​

La impronta de Twardowski, quien fuera a su vez discípulo de Franz Brentano, fue decisiva: implantó en Leópolis el ideal de una filosofía rigurosa y de prosa transparente, a la vez que introdujo elementos de lógica matemática en sus cursos (1899/1900), lo que atrajo a jóvenes como Łukasiewicz hacia el terreno formal. Este, ya desde 1904, leyó con intensidad The Principles of Mathematics de Bertrand Russell, cuyo influjo empujó su giro antipsicologista y la concepción de la lógica como disciplina exacta.^[1]​^[2]​

La atmósfera intelectual de Leópolis, en la frontera entre la filosofía y las matemáticas, favorecería el intercambio de Łukasiewicz con figuras como Wacław Sierpiński, Tadeusz Kotarbiński, Kazimierz Ajdukiewicz o Zygmunt Zawirski, quienes, directa o indirectamente, participaron de los primeros seminarios de lógica moderna en la ciudad. Twardowski y sus alumnos —entre ellos Łukasiewicz— articularon así el núcleo de la futura Escuela de Leópolis-Varsovia.^[2]​

Tras el doctorado, Łukasiewicz trabajó como profesor particular y empleado de biblioteca en la Universidad de Leópolis. En 1904 obtuvo una beca del gobierno autónomo de Galitzia que le permitió realizar estancias académicas en Berlín y Lovaina, reforzando su contacto con la lógica formal de raíz fregeano-russelliana. En 1906 alcanzó la habilitación con una memoria sobre causalidad titulada “Analiza i konstrukcja pojęcia przyczyna” (Análisis y construcción del concepto de causa, en español),^[3]​ la cual marcó su entrada como Privatdozent de Filosofía y le facultó para impartir cursos regulares. Ese mismo otoño dictó su primer ciclo.^[1]​ En esos años publicó además una buena cantidad de artículos breves que anuncian su doble perfil, histórico y formal: desde reseñas críticas hasta notas sobre inducción y la psicologización de la lógica.^[4]​^[5]​

Convertido en docente universitario desde 1906, Łukasiewicz fue el primer alumno de Twardowski que se incorporó a su claustro, aumentando la oferta local de cursos de lógica avanzada. En 1910 publicó una monografía centrada en el principio de no contradicción en Aristóteles y en la tradición posterior,^[6]​ acompañada de un importante apéndice que popularizaba la lógica algebráica de Louis Couturat. Aunque bastante elemental en lo matemático, la obra operó como palanca de institucionalización de la lógica entre los filósofos del Leópolis.^[1]​^[2]​

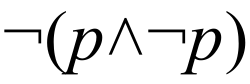
A la par, se incubaron dudas sobre la bivalencia y el tercio excluso. Tras una visita a Graz y el contacto con la ontología de Alexius Meinong, Łukasiewicz sostuvo ya en 1910 que el tercio excluso no es “fundamental” en un sentido estrictamente lógico y que su aplicación se correlaciona con supuestos deterministas. Esbozó así el horizonte de una lógica trivalente que, años después, cristalizaría en su ${\displaystyle {\text{Ł}}_{3}}$.^[1]​

Este sustrato filosófico —favorable a una metodología exacta, una atención a la historia de la lógica y la apertura a sistemas no clásicos— define el perfil del joven Łukasiewicz en el final de su etapa gallego-austríaca. Ya en 1906, Łukasiewicz era definible como lo que la literatura llama un filósofo "logicoidal”,^[7]​ para quien los grandes sistemas (i.e., Platón, Aristóteles, Descartes, Spinoza, Kant, Hegel) no resisten el escrutinio de la precisión logística; una tesis que remite a su ulterior defensa de una filosofía reconstruida axiomáticamente.^[8]​

La Primera Guerra Mundial propició el traslado del eje académico: en 1915, con el beneplácito de las autoridades ocupantes, se reabrió la Universidad de Varsovia en lengua polaca y Łukasiewicz fue nombrado profesor de filosofía. Sus cursos —de lógica elemental y avanzada, historia de la filosofía y metodología de las ciencias deductivas— atrajeron a jóvenes matemáticos e impulsaron la naciente Escuela Polaca de Matemáticas.^[2]​ Kazimierz Kuratowski dejó un testimonio minucioso del impacto de esas clases: el análisis de consistencia e independencia de axiomas, y críticas a textos como la Aritmética teórica (1912) de Stanisław Zaremba,^[9]​ suscitaron un debate metodológico (1916–1918) que afinó conceptos como cantidad, orden y par ordenado.^[10]​

Ese entorno —Varsovia y Leópolis—, articulado por el programa de investigación matemática y la revista Fundamenta Mathematicae (desde 1920), consolidarían una cultura de investigación concertada en teoría de conjuntos, topología y lógica, con la lógica ganando centralidad en el método matemático polaco. Este programa fue el plan estratégico impulsado por Zygmunt Janiszewski hacia 1915–1920 para organizar la investigación matemática en la Polonia renacida. Sus ejes fueron: (i) concentrar esfuerzos en áreas elegidas (pronto entendidas como teoría de conjuntos y topología, con aplicaciones), (ii) —inicialmente— trabajar “como un solo grupo fuerte” (este segundo punto se abandonó pronto), y (iii) crear una revista especializada en lenguas internacionales, realizada en Fundamenta Mathematicae (primer volumen en 1920). El programa, además, asignó un papel central a la lógica y a los fundamentos, lo que se reflejó en Varsovia en pasos organizativos (e.g., creación de cátedras y presencia exponenciald de docencia sistemática sobre los temas) y en el proyecto inicial de dividir Fundamenta en dos series (conjuntos/topología y lógica/fundamentos). La junta editorial incluía a Stefan Mazurkiewicz, Wacław Sierpiński, Stanisław Leśniewski y el propio Łukasiewicz.^[1]​

Con la independencia de Polonia (1918), Łukasiewicz fue llamado a tareas de Estado. Actuó como Ministro de Cultos y Educación Pública en el gobierno de Ignacy Jan Paderewski, antes de retornar en 1919 a la Universidad de Varsovia e integrar —como ya se ha adelantado— el consejo editorial de Fundamenta Mathematicae.

En ese mismo período enuncia públicamente la idea de una lógica trivalente. Łukasiewicz expuso por primera vez el sistema ${\displaystyle {\text{Ł}}_{3}}$ en su “lección de despedida” del 7 de marzo de 1918 en el Aula Magna de Varsovia,^[11]​ alegando que en el verano de 1917 había trabajado el cálculo en detalle^[12]​ (la presentación formal llegaría en 1920 con “O logice trójwartościowej” [Sobre la lógica trivalente, en español]).^[13]​ La motivación filosófica era inequívoca: el problema de los futuros contingentes (ya augurado en el cap. 9 del De Interpretatione de Aristóteles) y su conexión con el determinismo. Para Łukasiewicz, romper el vínculo entre bivalencia y necesidad implica introducir, junto a la verdad y la falsedad, un tercer valor —la posibilidad— que evite que toda predicción verdadera sobre lo futuro sea también necesaria.

El periodo de entreguerras fue su etapa más fecunda del lógico polaco. Łukasiewicz se convirtió, junto a Stanisław Leśniewski y Alfred Tarski, en una de las figuras centrales de la Escuela de Lógica de Varsovia. Ejerció el rectorado de la Universidad en dos ocasiones (1931/32 y 1932/33), tras haber sido decano y vicerrector. En 1928 contrajo matrimonio con Regina Barwińska (1890–1990), profesora y escritora.^[1]​

Recibió numerosos honores: el Gran Comendador de la Orden de Polonia Restituta (1923), el Gran Comendador de la Orden del Mérito de Hungría (1935), el doctorado honoris causa por la Universidad de Münster (1938), y la membresía en la Academia Polaca de Artes y Ciencias (Cracovia) y en sociedades científicas de Leópolis y Varsovia. Dirigió las tesis doctorales de Mordechaj Wajsberg, Zygmunt Kobrzyński, Stanisław Jaśkowski, Bolesław Sobociński y Jerzy Słupecki.^[1]​

En el plano doctrinal, retomó en 1922 su argumentación contra el determinismo en la lección inaugural como rector (16 de octubre de 1922), que evolucionaría hasta su versión publicada póstumamente (“On Determinism”, 1961).^[8]​ Allí defendió que, si una predicción sobre un hecho futuro contingente es verdadera en el momento de su enunciación, el acontecimiento deviene necesario; de modo que, para preservar la libertad, hay que negar la verdad en ese momento y asignar la posibilidad como tercer valor de verdad.^[1]​

Por esos años formuló asimismo las tablas de verdad para sistemas con finitos o infinitos valores (1922),^[15]​ abriendo la vía que, décadas después, se relacionaría con la llamada lógica difusa. Su valoración, no exenta de autoconfianza, comparaba el descubrimiento de lógicas multivalentes con el de las geometrías no euclidianas.^[16]​

La invasión de Polonia (septiembre de 1939) fue devastadora para su vida y su obra. La Luftwaffe bombardeó su casa y destruyó su biblioteca, papeles y correspondencia, donde apenas sobrevivió un volumen de separatas. La Universidad de Varsovia fue clausurada y Łukasiewicz aceptó un empleo modesto en los Archivos de la ciudad de Varsovia. Impartió clases en la Universidad clandestina y recibió ayuda económica de Heinrich Scholz, único catedrático de lógica matemática en Alemania y su aliado académico. El clima de sospecha —existiendo acusaciones de pro-germanidad o antisemitismo por parte de algunos colegas— y el temor ante la inminente ocupación soviética a finales de 1943 precipitaron su decisión de abandonar el país.^[1]​

La red alemana de Scholz resultó crucial. Gestionó un permiso de viaje a Münster como etapa previa a un eventual destino en Suiza. Łukasiewicz y su esposa salieron de Varsovia el 17 de julio de 1944, dos semanas antes del Alzamiento de Varsovia. El atentado contra Adolf Hitler del 20 de julio bloqueó toda posibilidad de salida a Suiza y, entre julio de 1944 y enero de 1945, la pareja sobrevivió a los bombardeos aliados en Münster, hasta que Jürgen von Kempski los acogió en su granja de Hembsen (Kreis Höxter), donde fueron liberados por tropas estadounidenses el 4 de abril de 1945.^[1]​ Una narración paralela, basada en testimonios próximos al círculo de Scholz, añade detalles materiales de esas semanas —e.g., vida en sótanos de viviendas destruidas, traslados ocasionales a pisos vacíos por intercesión del profesor de Münster— y de los primeros pasos tras la liberación, como fue el contacto con el general Leon Berbecki y una experiencia docencia de lógica en un instituto para desplazados en Hohenwöpel.^[17]​

Tras la liberación de abril de 1945, Łukasiewicz enseñó lógica en un liceo polaco instalado en un antiguo campo de prisioneros (Oflag VI B, Dössel). En octubre de 1945 se le autorizó viajar a Bruselas, donde enseñó en un intituto científico polaco provisional (no confundir con la Academia Polaca de Ciencias). Allí entró en contacto con emisarios —el enigmático “teniente Herbert”— que ofrecían a científicos de Europa Central la posibilidad de reubicarse en Irlanda. Łukasiewicz aceptó. Embarcó en Ostende el 1 de marzo de 1946, llegó a Londres y, por ferrocarril y barco, alcanzó Dublín con su esposa Regina el 4 de marzo . Al principio se alojaron en el Hotel Echo. Poco después fueron recibidos por el vicesecretario de Exteriores y, en julio de 1946, por el Taoiseach Éamon de Valera, que finalmente le nombró profesor de lógica matemática en la Royal Irish Academy (RIA).^[1]​^[17]​

En Irlanda, Łukasiewicz halló un refugio tardío y un espacio de investigación ajeno a la docencia. Desde el otoño de 1946 impartió conferencias semanales en la RIA y, pese a la debilidad de su salud, reanudó lazos con sus contactos internacionales. Participó —desde 1949— de congresos en Reino Unido, Francia y Bélgica; dictó clases de lógica matemática en Universidad de la Reina de Belfast y de silogística aristotélica en la University College Dublin. En 1949, tuvo oportunidad de tratar con Carew Arthur Meredith y Father Gwynn. En febrero de 1950 viajó a Mánchester, donde se encontró con Czesław Lejewski y conversó con Alan Turing sobre su notación sin paréntesis. En 1955, el Trinity College Dublin lo invistió con el doctorado honoris causa. Desde el punto de vista científico, su decenio dublinés produjo importantes aportes: axiomas ultracortos para el cálculo proposicional; functores proposicionales variables; y un sistema modal propio (el sistema Ł).^[1]​^[17]​

Las relaciones epistolares documentan, además, su inserción en la vida académica irlandesa. En mayo de 1954, con motivo del centenario de The Laws of Thought de George Boole (organizado por la RIA), se publicaron en las Proceedings cuatro cartas entre Łukasiewicz, Bertrand Russell, Garrett Birkhoff e Józef Maria Bocheński. El propio Łukasiewicz no pudo asistir al homenaje, y su misiva —publicada el 15 de noviembre de 1955— figura al inicio del dossier con los textos de Geoffrey Taylor, Rush Rhees, Robert Feys, Luitzen Egbertus Jan Brouwer, John Barkley Rosser y otros.

Bertrand Russell

Garrett Birkhoff

Józef Maria Bocheński

Volviendo sobre su desmejorado estado de salud, la guerra había dejado secuelas cardiacas (acarriaba angina de pecho diagnosticada ya en Varsovia), que le obligaron a reducir su actividad docente —de hecho, en los años de la universidad clandestina cedió parte de sus clases a Bolesław Sobociński— y que reaparecieron con fuerza en los años cincuenta.^[17]​

El 13 de febrero de 1956, tras una operación de vesícula biliar, una trombosis coronaria acabó con su vida en Dublín. Fue enterrado en el cementerio Mount Jerome, con la inscripción “far from dear Lwów and Poland” en la lápida —una fórmula que condensa su destierro biográfico—. Su esposa Regina depositó la mayor parte de los papeles y correspondencia en la Royal Irish Academy. En 1963, la RIA trasladó el fondo a la biblioteca de la Universidad de Mánchester, en atención a Czesław Lejewski, discípulo que había vigilado la segunda edición de la silogística aristotélica (publicada póstumamente en 1957).^[18]​ Sus restos fueron repatriados en 2022 al cementerio de Powązki (Varsovia), resultado de una iniciativa del gobierno polaco.^[17]​

En el plano intelectual, sus años finales en Irlanda consolidaron y difundieron resultados característicos: desde la axiomática proposicional ultrabreve hasta los functores variables, pasando por un sistema modal de difícil recepción. El balance de Peter Simons, uno de los mayores expertos en Łukasiewicz, es matizado:^[1]​ mientras la matemática de las lógicas plurivalentes habilitada por Łukasiewicz floreció (incluso de forma reciente),^[19]​ su interpretación modal multivalente terminó siendo marginal. En cambio, su forma de hacer historiografía de la lógica inauguró una interacción fructífera entre pasado y presente (con su recuperación de los estoicos y Aristóteles), y su enseñanza en Varsovia ayudó a la catalización de innovaciones como la deducción natural de Stanisław Jaśkowski.^[20]​^[21]​^[22]​

En el plano onomástico, el planeta menor 27114 lleva el nombre Lukasiewicz, un reconocimiento típicamente asignado a científicos de talla internacional.^[23]​^[24]​

La obra lógica de Jan Łukasiewicz se caracteriza por tres grandes hitos:

1. Una reconstrucción axiomática extremadamente económica del cálculo proposicional, en paralelo con la invención y explotación de la notación polaca sin paréntesis;
2. La creación y desarrollo de lógicas polivalentes —desde ${\displaystyle {\text{Ł}}_{3}}$ hasta familias finitas ${\displaystyle {\text{Ł}}_{n}}$ e infinitas ${\displaystyle {\text{Ł}}_{\aleph _{0}}}$— al servicio de una concepción indeterminista de los “futuros contingentes”; y
3. Una ampliación del lenguaje proposicional mediante funtores proposicionales variables, junto con un giro de investigación modal y varios resultados metateóricos (v.gr. independencia, completitud, axiomatizaciones mínimas).

Sus métodos —sobre todo, el uso sistemático de matrices de verdad— y sus criterios normativos —pocas primitivas, axiomas cortos e independientes— marcaron el estilo técnico de la Escuela de Leópolis-Varsovia.

En la década de 1920, Łukasiewicz y sus colaboradores (Alfred Tarski, Adolf Lindenbaum, Jerzy Słupecki, Bolesław Sobociński, Mordechaj Wajsberg, entre otros) convirtieron el cálculo proposicional en un campo de competición por la perfección lógica. De lo que se trataba era de minimizar primitivas, acortar axiomas, asegurar independencia y buscar axiomas únicos para sistemas completos. Este “deporte” polaco, lejos de ser trivial, respondía a un ideal de exactitud: “lógica por la lógica misma”.^[1]​

El manual Elements of Mathematical Logic (publicado originalmente en 1929) expone su tratamiento maduro del cálculo bivalente clásico: el sistema toma como primitivas sólo la implicación C y la negación N, y adopta un conjunto elegante de tres axiomas (en notación polaca):^[25]​

1. ${\displaystyle CCpqCCqrCpr}$,
2. ${\displaystyle CCNppp}$,
3. ${\displaystyle CpCNpq}$.

más tres reglas: modus ponens, sustitución uniforme y reemplazo definicional. Con esta base y una notación lineal extremadamente comprimida para las demostraciones, obtiene unos 140 teoremas en poco más de una decena de páginas.^[1]​

Metodológicamente decisivo fue su empleo de matrices de verdad para establecer independencia y para probar completitud de varios cálculos: el completo (conectivos funcionalmente completos), el puramente implicacional y el puramente equivalencial. Un hito es la demostración de que el cálculo equivalencial puede fundarse en un único axioma,

${\displaystyle EEpqErqEpr}$,

con reglas de sustitución y desprendimiento (detachment) para equivalencia; y que ningún axioma más corto basta como único fundamento. En el cálculo implicacional puro, tras mejoras de Wajsberg y del propio Łukasiewicz, éste mostró en 1936 que

${\displaystyle CCCpqrCCrpCsp}$

sirve como axioma único y que ninguno más corto resulta suficiente.^[4]​ El resultado se publicó en 1948.^[26]​

En el frente de la notación, Łukasiewicz impulsó la notación polaca sin paréntesis (prefix), que reduce ambigüedades estructurales y permite derivaciones lineales muy comprimidas. En su exposición de 1921 sobre “Logika dwuwartościowa” (Lógica bivalente, en español) introduce, además, símbolos constantes ‘1’ y ‘0’, y esboza un sistema de aserción () y rechazo (⊣) a nivel de lenguaje objeto, preludiando la tabulación veritativa en el propio cálculo; también cuantifica variables proposicionales al modo de Peirce, con ${\displaystyle \Pi }$ (universal) y ${\displaystyle \Sigma }$ (existencial).^[27]​

El clima de resultados fue sintetizado en el artículo escrito en 130 junto a Alfred Tarski, Untersuchungen über den Aussagenkalkül (Investigaciones sobre el cálculo sentencial, en español), que relevaba logros de generales de la Escuela de Leópolis-Varsovia en cálculos clásicos y multivalentes.^[28]​

La ruptura con la bivalencia en Łukasiewicz se origina en su reflexión sobre modalidad y futuros contingentes. En su “lección de despedida” (Varsovia, 17 de marzo de 1918)^[11]​ proclamó haber construido una lógica trivalente con un tercer valor — lo posible— que hace sitio a la libertad y al indeterminismo. Esa decisión filosófica reaparece, revisada, en su conferencia rectoral “On Determinism” (16 de octubre de 1922; publicada póstumamente en 1961).^[8]​

La presentación pública del sistema trivalente llegó en 1920 con O logice trójwartościowej (Sobre la lógica trivalente, en español),^[13]​ anunciando un tercer valor para resolver el estatuto de enunciados cuya verdad presente sobre hechos futuros no está decidida. La motivación y el contexto filosófico están ampliamente documentados: el tercer valor “posibilidad” desactiva el paso determinista de “si es ahora verdadero que ${\displaystyle p}$ ocurrirá, entonces necesariamente ${\displaystyle p}$”. Más allá del caso trivalente, en 1922 Łukasiewicz mostró cómo dar tablas de verdad para conectivos estándar con valores numéricos en ${\displaystyle [0,1]}$: ${\displaystyle \mid Np\mid }$ ${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle -}$ ${\displaystyle |p|}$ y ${\displaystyle \mid Cpq\mid }$ ${\displaystyle =}$ ${\displaystyle min}$${\displaystyle \{1,1}$ ${\displaystyle -\mid p\mid +\mid q\mid \}}$.^[15]​ Esto abría sistemas con ${\displaystyle n}$ valores finitos y sistemas infinitamente valentes, que décadas después se reconocerían como antecesores de la lógica difusa.^[1]​^[16]​ Ya para 1930, Łukasiewicz enfatizaba que, si se interpreta todo valor intermedio como “posible”, sólo dos clases parecen filosóficamente relevantes: el sistema trivalente (sin grados) y el infinitamente valente (con grados), siendo éste “preferible” por su analogía con la probabilidad; y es que, así, las relaciones con el cálculo de probabilidades quedaban abiertas.^[16]​ Sin negar el uso aristotélico del tercio excluso (e.g., ${\displaystyle p\lor \lnot p\ }$ como “tautología” en su lectura), ${\displaystyle {\text{Ł}}_{3}}$ reinterpreta el valor de enunciados del tipo “mañana habrá batalla naval” como indeterminado ahora, con una semántica que internaliza modalidad y temporalidad (aunque la notación no la haga explícita).^[1]​^[12]​ En los desarrollos originales de ${\displaystyle {\text{Ł}}_{3}}$, la deducibilidad se obtenía con dos reglas: separación (modus ponens) y sustitución. Esto sitúa a ${\displaystyle {\text{Ł}}_{3}}$ en el grupo de teorías que, antes de Tarski (1936),^[29]​ concebían la consecuencia en términos de derivabilidad.^[12]​

Además del cálculo con funtores constantes (como ${\displaystyle N}$, ${\displaystyle C}$), Łukasiewicz propone funtores proposicionales variables (de uno o más lugares) que toman argumentos proposicionales.^[30]​ Esta idea, cercana a la protética de Stanislaw Leśniewski (quien introdujo también la cuantificación sobre variables proposicionales y functoriales),^[31]​ incrementa la potencia expresiva del sistema: una tesis de la protética reza, dejando implícitos los cuantificadores universales prefijados ${\displaystyle CEpqC}$${\displaystyle \delta }$${\displaystyle p}$${\displaystyle \delta }$${\displaystyle q}$, donde ${\displaystyle \delta }$ es un functor unario.

Cuando el lugar de argumento no es terminal en el contexto (e.g., ${\displaystyle Cpq}$) o la variable debe insertarse en más de un lugar (e.g., ${\displaystyle CCp0p}$), las definiciones auxiliares usadas para “mover” la posición del argumento resultan engorrosas. Łukasiewicz objetó este andamiaje y propuso su sustitución con apóstrofo: cualquier contexto con una variable proposicional libre puede servir como sustituendo de ${\displaystyle \delta }$; se marcan con apóstrofos los lugares de inserción del argumento y se realiza la sustitución in situ (p. ej., ${\displaystyle C'q,CC'0'}$). Con ello, las definiciones y los esquemas adoptan una forma implicacional directa y algebraicamente manejable.^[1]​

La compresión deductiva que habilita este dispositivo culmina en resultados (citados por el propio Łukasiewicz) debidos a Carew Arthur Meredith sobre funtores proposicionales variables:^[30]​ (i) todo el cálculo proposicional clásico con funtores variables se axiomatiza con el único axioma ${\displaystyle C}$${\displaystyle \delta }$${\displaystyle pC}$${\displaystyle \delta }$${\displaystyle Np}$${\displaystyle \delta }$${\displaystyle q}$; y (ii) en presencia de cuantificadores y funtores variables basta ${\displaystyle C}$${\displaystyle \delta }$${\displaystyle \delta }$${\displaystyle 0}$${\displaystyle \delta }$${\displaystyle p}$.^[1]​

Desde 1918, Łukasiewicz contempló la modalidad en clave de grados de posibilidad, lo que favorecía ${\displaystyle {\text{Ł}}_{3}}$ y, en última instancia, ${\displaystyle {\text{Ł}}_{\aleph _{0}}}$.^[11]​ Esta posoción permanecería sin mayores cambios en sus escritos inmediatos hasta, por lo menos, la década de 1930.^[13]​^[15]​^[16]​^[32]​ Sin embargo, hacia 1951–1952, mientras trabajaba sobre la lógica modal aristotélica, revisó su planteamiento: observó que en ${\displaystyle {\text{Ł}}_{3}}$ aparecen teoremas de la forma ${\displaystyle L\alpha }$ (por ejemplo, ${\displaystyle LCpp}$), consecuencia que juzgó problemática.^[33]​^[34]​^[35]​ Esta reconsideración lo condujo a formular un sistema modal Ł alternativo, con nuevas restricciones sobre la propagación de la necesidad.^[1]​

La trayectoria modal de posguerra incluye, además, “On the intuitionistic theory of deduction” (1952), donde propone una axiomatización elegante de la lógica intuicionista usando letras ${\displaystyle F,T,O}$ para evitar colisiones con conectivos clásicos, y muestra cómo definir la implicación clásica como ${\displaystyle NTpNq}$, formulando la definición con funtores variables. En esta versión, la lógica clásica basada en ${\displaystyle C}$, ${\displaystyle N}$ queda contenida en la intuicionista si el detachment se limita a fórmulas en ${\displaystyle C}$, ${\displaystyle N}$.^[36]​ El programa se completa con textos como “Arithmetic and modal logic” (1954), que exploran el entrelazamiento entre sistemas modales y estructuras aritméticas.^[37]​

Łukasiewicz emplea matrices de verdad (extendidas más allá de dos valores) como disposictivos ${\displaystyle M=\langle A,B,f,g,\ldots \rangle }$, donde ${\displaystyle A}$ es el conjunto de valores, ${\displaystyle B\subseteq A}$ el conjunto de valores designados, y ${\displaystyle f,g,\ldots }$ interpretan los funtores. En su lectura clásica de 1922/23, las funciones para negación e implicación vienen dadas por ${\displaystyle \mid Np\mid }$ ${\displaystyle =}$ ${\displaystyle 1}$ ${\displaystyle -}$ ${\displaystyle |p|}$ y ${\displaystyle \mid Cpq\mid }$ ${\displaystyle =}$ ${\displaystyle min}$${\displaystyle \{1,1}$ ${\displaystyle -\mid p\mid +\mid q\mid \}}$.^[15]​ Esta parametrización abre tanto los sistemas ${\displaystyle {\text{Ł}}_{n}}$ (finitos) como el sistema infinitamente valente ${\displaystyle {\text{Ł}}_{\aleph _{0}}}$. En términos metodológicos, las matrices permiten fabricar contraejemplos semánticos para demostrar independencia de axiomas y, en sentido positivo, fundamentar pruebas de completitud para distintos cálculos proposicionales.^[1]​^[12]​^[17]​

Con esta técnica, Łukasiewicz (y su círculo) estableció independencia en sistemas fregeanos y russellianos, y demostró completitud para el cálculo proposicional completo, el implicacional puro y el equivalencial. Además, mostró que el cálculo equivalencial puede basarse en un único axioma y que no hay ninguno más corto que pueda servir de único fundamento. Análogamente, identificó un axioma único para el implicacional puro, con pruebas de minimalidad por longitud. Estas conclusiones sintetizan el modo en que las matrices se vuelven una herramienta metateórica de primera línea: a la vez constructiva (validación) y destructiva (independencia).^[1]​

En el cálculo equivalencial, el artículo de 1939 titulado Der Äquivalenzkalkül (El cálculo equivalencial, en español) fijó el terreno técnico: allí se registra el axioma único ${\displaystyle EEpqErqEpr}$, con sustitución y detachment para E, y la prueba de que no existe un axioma único más corto para el sistema. El texto quedó inédito por la guerra (sobrevivió un offprint en Münster) y fue traducido y reeditado después en sus Selected Works.^[38]​

En el cálculo implicacional puro, Łukasiewicz descubrió en 1936 que la fórmula ${\displaystyle CCCpqrCCrpCsp}$ sirve de axioma único, y demostró de nuevo la minimalidad por longitud; la publicación del resultado se demoró hasta 1948 en las Proceedings of the Royal Irish Academy,^[26]​ y recibió un desarrollo adicional en 1950.^[39]​

Un segundo eje de su programa metateórico fue internalizar el comportamiento de las tablas de verdad en el propio lenguaje objeto. Łukasiewicz introduce, junto a la aserción (${\displaystyle \vdash }$), la rechazabilidad (${\displaystyle \dashv }$) y las constantes proposicionales ‘${\displaystyle 1}$’ y ‘${\displaystyle 0}$’, de modo que la tabulación de la implicación ${\displaystyle C}$ queda expresada por cuatro principios del lenguaje objeto: ${\displaystyle \vdash C00,\ \vdash C01,\ \dashv C10,\ \vdash C11}$, con ${\displaystyle \vdash }$${\displaystyle 1}$ y ${\displaystyle \dashv }$${\displaystyle 0}$ como “primeros principios”. El artículo cuantifica además variables proposicionales al modo de Peirce (${\displaystyle \Pi }$, ${\displaystyle \Sigma }$). Esta estrategia permite “hacer tablas” desde dentro, sin recurrir aún a un metalenguaje semántico.^[27]​

Finalmente, el propio Łukasiewicz explicita la función metodológica de las matrices en su contribución a los Entretiens de Zurich.^[40]​ Allí presenta las matrices lógicas y sus aplicaciones a la independencia axiomática. En su manual de 1929^[25]​ y en el artículo conjunto con Tarski de 1930^[28]​ este enfoque ya aparece operativo: el estilo polaco de “pocos axiomas, muy cortos, independientes” y la búsqueda de axiomas únicos sostienen una estética de precisión que precede el giro semántico posterior en la noción de consecuencia.

Aun manteniendo la neutralidad metafísica de la lógica, Łukasiewicz defendió la extensionalidad como tesis metodológica: las oraciones denotan valores (verdad/falsedad, o valores adicionales), y la lógica es la ciencia de esos valores, no de juicios psicológicos ni de “contenidos” proposicionales. Hacia finales de los años treinta, su convicción adquiere un sesgo platónico, formulado en una defensa de la “logística”: al trabajar, por ejemplo, en el problema del axioma más corto, siente la lógica como una estructura resistente que se descubre, no se inventa.^[41]​

Además de sus aportes técnicos, Łukasiewicz es considerado un pionero en el modo moderno de escribir historia de la lógica: reconstruir sistemáticamente los sistemas antiguos desde la lógica formal moderna. Este enfoque exige dominar las herramientas contemporáneas (i.e., axiomatización, tablas de verdad, reglas explícitas) para clarificar los logros y los límites de las doctrinas clásicas. En su entrada de la Stanford Encyclopedia of Philosophy, Peter Simmons lo resume con precisión: “puede considerársele el padre del modo moderno de hacer historia de la lógica […] ‘desde el punto de vista de la lógica formal moderna’”.^[1]​

El programa historiográfico de Łukasiewicz estuvo acompañado de una crítica severa a la historiografía anterior (e.g., la realizada por Karl von Prantl o Eduard Zeller): “La historia de la lógica debe escribirse de nuevo, y por un historiador que domine a fondo la lógica matemática moderna […] desde el punto de vista lógico [la obra de Prantl] es prácticamente inútil".^[42]​ En términos metodológicos, esto implicaba separar la erudición filológica del análisis lógico formal, y reconstruir los sistemas con lenguaje y reglas explícitas, incluso a costa de introducir notación y axiomas que Aristóteles o los estoicos no escribieron, pero que presuponían.

La primera etapa de Łukasiewicz como historiador está marcada por su libro de 1910 O zasadzie sprzeczności u Arystotelesa (Sobre el principio de contradicción en Aristóteles, en español), que ya revela su tendencia a sondear “el corazón de los textos” más que a repetir interpretaciones tradicionales.^[43]​ El corpus maduro llega en 1951 con Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic,^[18]​ obra que revolucionó los estudios del Organon. Según el relato detallado de la SEP, su génesis incluye: una conferencia en Cracovia (1939), un manuscrito polaco destruido en el bombardeo de Varsovia, y el curso de 1949 en University College Dublin como base del libro. La segunda edición de Aristotle’s Syllogistic from the Standpoint of Modern Formal Logic (1959) incorpora tres capítulos sobre la silogística modal, ya con el sistema Ł.^[1]​

Łukasiewicz formaliza la silogística con cuatro expresiones categóricas (Aab, Eab, Iab, Oab), tomando ${\displaystyle A}$ e ${\displaystyle I}$ como primitivas y definiendo ${\displaystyle E=NI}$ y ${\displaystyle O=NA}$. El sistema añade a la lógica proposicional un par de leyes de identidad (${\displaystyle \vdash Aaa}$, ${\displaystyle \vdash Iaa}$) y como esquemas axiomáticos a Barbara (${\displaystyle \vdash CKAbcAabAac}$) y Datisi (⊢CKAbcIbaIac), con modus ponens y sustitución sobre variables de término. A ello suma formas rechazadas (con ${\displaystyle \dashv }$) para obtener las 232 combinaciones inválidas de Aristóteles. El veredicto de Łukasiewicz —recogido por Simons— es célebre: pese a su estrechez, la silogística “es un sistema cuya exactitud supera incluso a la de una teoría matemática”.^[1]​

En su análisis, Łukasiewicz corrige errores arraigados. Denuncia, por ejemplo, la traducción de ὅρος (horos) como Begriff (“concepto”), que sugiere una psicologización ajena al texto aristotélico. También insiste en que la silogística trata relaciones entre términos generales, no con respecto a individuos (de ahí la impropiedad del ejemplo “Sócrates…” como paradigma escolar). También restituye el carácter condicional de los esquemas aristotélicos: no afirman las premisas ni la conclusión, usan vínculos condicionales entre formas. Finalmente, rastrea el malentendido histórico que atribuye a Galeno la cuarta figura de silogismos simples: Galeno introdujo una “cuarta figura” entre silogismos complejos, no en los simples. El gran aporte de Łukasiewicz es señalar que Aristóteles conocía los modos hoy asignados a la cuarta figura, aunque no la distinguió como tal.^[44]​ Esta reconstrucción —coronada por la axiomatización del sistema con términos primitivos, axiomas (modos como Barbara o Datisi) y reglas (sustitución, detachment, reemplazo definicional)— ofrece una forma “plena y final” de la silogística categórica, coherente con el espíritu del Organon y compatible con una lógica proposicional previa como antecedente.

El descubrimiento decisivo en la trayectoria historiográfica de Łukasiewicz fue el reconocimiento de la lógica estoica como un cálculo proposicional temprano, y no como una versión empobrecida de la silogística aristotélica. Preparando el examen de una tesis sobre los estoicos, leyó fuentes originales y concluyó —contra Prantl, Zeller y la ortodoxia decimonónica— que los “indemostrables” estoicos constituyen reglas proposicionales: el primero de ellos (“si el primero, entonces el segundo; pero el primero; por tanto, el segundo”) es un modus ponens; y sus “variables” (indicadas por numerales ordinales) son proposicionales, no de término. Llevó estas ideas a una reunión académica en Leópolis en 1923.^[1]​ Su exposición sistemática apareció en 1934 con Z historii logiki zdań (Sobre la historia de la lógica de las proposiciones, en español).^[42]​

Aquí, Łukasiewicz recorre cuestiones antiguas sobre el condicional, la formulación implícita de las leyes de Agustus De Morgan en Pedro Hispano y Guillermo de Ockham, y la teoría medieval de las consecuencias, hasta Frege y los cálculos proposicionales modernos. El aprecio moderno de la lógica estoica data de la clarificación de Łukasiewicz y su elogio explícito —en particular de Crisipo de Solos—, a la par que critica a Prantl por carecer del entendimiento de una lógica posfregeana que le permitiera interpretar debidamente las fuentes.^[1]​

La reconstrucción técnica estoica que atribuye Łukasiewicz incluye el principio de identidad (tomado de Sexto Empírico) formalizable como “si ${\displaystyle p}$, entonces ${\displaystyle p}$”; el listado de cinco axiomas transmitidos por Galeno —el primero es justamente el modus ponens—; y una exégesis que disipa la lectura despectiva de Prantl al mostrar el significado lógico de esas formas. Tadeusz Kotarbiński añade que Peirce había avisado antes el carácter proposicional de la lógica estoica, pero atribuye a Łukasiewicz la investigación de fuentes y la victoria historiográfica “en todo el frente”.^[44]​

El nexo entre historia y lógica en Łukasiewicz es estrecho. Según Kotarbiński, la motivación que lo llevó a reexaminar a Aristóteles fue análoga a la que guio su invención de la lógica polivalente: así como la transformación del V Postulado generó geometrías no euclidianas, la transformación/omisión del principio de no contradicción sugería la posibilidad de una lógica no aristotélica. De este modo, su investigación histórica surge del mismo problema de fondo que su obra lógica, y ambas se retroalimentan: el análisis de Aristóteles y los estoicos prepara su avance en lógicas no clásicas y, recíprocamente, sus herramientas de la lógica moderna iluminan las obras de los antiguos.

Se puede decir que la historiografía de Łukasiewicz articula tres tesis duraderas que definen el arco clásico de su “historia de la lógica”:

1. Que Aristóteles produjo un sistema de precisión extraordinaria, susceptible de axiomatizarse con primitivos y reglas explícitas, lejos del psicologismo;
2. Que los estoicos sentaron elementos de un cálculo proposicional, y que su aparato (i.e., indemostrables, variables) debe leerse lógicamente; y
3. Que hacer historia de la lógica exige lógica, i.e., herramientas formales contemporáneas y la actitud de reescribir críticamente las tradiciones.

Desde su consolidación en Varsovia (1915–1939) —con rectorados y dirección académica—, Łukasiewicz ejerció de catalizador: su curso y seminario de lógica formaron cuadros técnicos (entre ellos, Jerzy Słupecki, Bolesław Sobociński, Czesław Lejewski) que prolongaron su impronta en calculo equivalencial, implicacional y matrices multivalentes. La caracterización de Peter Simons destaca su papel como primer historiador de la lógica que aplica lógica moderna al pasado y como arquitecto temprano de la escuela de Varsovia.^[1]​

Las cartas y colaboraciones con Heinrich Scholz (Münster) ilustran la densidad de redes centroeuropeas: Scholz intercedió en trámites administrativos, propició estancias y mantuvo un intercambio técnico e institucional de largo aliento. La reconstrucción detallada de esas relaciones confirma apoyos concretos en los años 1943–46 y el rol de Scholz como pivote alemán para lógicos polacos desplazados.^[4]​

En el exilio irlandés (1946–1956), la Royal Irish Academy (RIA) le ofreció una plataforma para conferencias y difusión pública. La RIA y la prensa académica irlandesa documentan la exposición conmemorativa de 2022 que repasó su década dublinesa y la reciente repatriación de sus restos a Varsovia (Powązki), señal de una memoria cívica activa.^[45]​^[46]​

El dossier del centenario de George Boole consignado en las Proceedings of the Royal Irish Academy muestra una recepción entre pares internacionales —cartas cruzadas con Bertrand Russell, Garrett Birkhoff e Józef Maria Bocheński, junto a contribuciones de Geoffrey Taylor, Rush Rhees, Robert Feys, L. E. J. Brouwer y J. B. Rosser— que sitúa a Łukasiewicz como interlocutor de la filosofía analítica y la matemática del momento.^[47]​

Los discípulos y allegados inmediatos constituyen el primer anillo de su legado. Jerzy Słupecki sistematizó el cálculo equivalencial y exploró matrices para independencia. Bolesław Sobociński trabajó en compresión axiomatizante (implicacional puro) y en estructuras de deducción con detachment. Czesław Lejewski contribuyó a la ontología formal y custodió la edición póstuma de Aristotle’s Syllogistic (2.ª ed., 1957), además de vigilar la transferencia del archivo a Mánchester. Estos vectores están inventariados en biografías técnicas y cronologías.^[1]​

Más ampliamente, el entorno de la Escuela de Leópolis-Varsovia (sustantivamente Kazimierz Twardowski, Stanisław Leśniewski y Alfred Tarski) fue terreno fértil para la semántica y la metalógica. Jan Woleński ha descrito con precisión la recepción y consolidación de la lógica en Polonia (1870–1920), enfatizando la transición hacia métodos axiomáticos y metateóricos que luego habilitaron la semántica de matrices y la exactitud historiográfica practicada por Łukasiewicz.^[2]​ En tensión productiva con el intuicionismo y con corrientes alemanas, el “estilo polaco” —basado en la claridad, formalización y búsqueda de axiomas cortos— se convirtió en seña de identidad de la escuela.

La notación polaca (prefija, sin paréntesis) devino en un emblema de economía sintáctica. Su reverso (RPN) se popularizó en computación a partir de los años cincuenta, con trabajos como los de Charles Leonard Hamblin. La documentación lexicográfica y técnica sitúa la acuñación de la notación polaca inversa en 1957, integrando así al legado de Łukasiewicz una interfase práctica con lenguajes y máquinas.^[48]​

El vector modal (de ${\displaystyle {\text{Ł}}_{3}}$ al Ł-modal “tardío”) fue leído y discutido por la tradición anglosajona. Arthur Prior, al sistematizar la lógica temporal, reconoció influencias polacas (notación y estrategias axiomáticas) en Time and Modality (1957)^[49]​ y Past, Present and Future (1967).^[50]​

En paralelo, la historiografía lógico-aristotélica de Łukasiewicz rehízo estándares filológicos. La segunda edición ampliada de Aristotle’s Syllogistic obtuvo reseñas técnicas en revistas de primer nivel y aseguró su canonicidad en filología clásica y lógica formal.^[51]​^[52]​

Tras su fallecimiento en Dublín (1956), la RIA conservó papeles y correspondencia. En 1963, por razones prácticas y mediación académica (realizada fundamentalmente por Czesław Lejewski), el fondo pasó a la biblioteca de la Universidad de Mánchester. La propia institución británica ha documentado el "redescubrimiento" del fondo y su relevancia para investigar la diáspora polaca y la historia de la lógica del siglo XX.^[53]​

En 2022, una exposición en la RIA reanudó la conexión irlandesa y sirvió de antesala a la repatriación de los restos a Varsovia (reinhumación que fue realizada en el Cementerio de Powązki, el 22 de noviembre de 2022), con cobertura institucional y periodística.^[45]​^[46]​ Este arco de preservación y homenaje materializa la continuidad de su memoria pública.

El paso decisivo en la recepción técnica es la algebraización del ${\displaystyle {\text{Ł}}_{\aleph _{0}}}$ proposicional. Chang demostró la completitud del cálculo infinitamente valente introduciendo las MV-álgebras como semántica algebraica natural. Su artículo fundacional en Transactions of the AMS (1958) fijó el diccionario entre operaciones lógicas (${\displaystyle \neg }$, ${\displaystyle \oplus }$) y operaciones algebraicas, inaugurando una teoría estructural fértil.^[54]​

Sobre esta base se erigió una teoría estructural rica. La monografía de Cignoli, D’Ottaviano y Mundici, titulada Algebraic Foundations of Many-Valued Reasoning (2000), sistematiza el campo, contadn con: (i) equivalencia categórica entre MV-álgebras y ciertas ℓ-grupos con unidad fuerte; (ii) análisis de variedades y propiedades reticulares; (iii) desarrollo de la versión ${\displaystyle \infty }$-valente de Łukasiewicz (Ł${\displaystyle \infty }$) como teoría central.^[55]​

La equivalencia MV${\displaystyle \leftrightarrow }$Wajsberg ha sido refinada en la literatura posterior,^[56]​^[57]​^[58]​ reforzando la idea de que la lógica de Łukasiewicz posee una semántica algebraica robusta con vías de generalización (quasi-MV, Heyting–Wajsberg, etc.). Esta línea ancla el legado de Łukasiewicz en el mainstream del álgebra universal contemporánea.

La interpretación numérica de 1922/23^[15]​ —conectivos de Łukasiewicz como funciones sobre ${\displaystyle [0,1]}$— anticipa una semántica continua que décadas después cristaliza en lógicas de t-normas. Petr Hájek unificó este campo en Metamathematics of Fuzzy Logic (1998) donde la lógica de Łukasiewicz aparece como caso paradigmático:^[59]​ su t-norma ${\displaystyle (x\otimes y)=\max\{0,\,x+y-1\}}$ y la implicación asociada sintetizan el modelo fuzzy de matriz łukasiewicziana. El lugar de Łukasiewicz en las lógicas difusas y plurivalentes se recoge, además, en entradas de la Stanford Encyclopedia of Philosophy, que explicitan la semántica algebraica vía MV-álgebras y su rol estructural en la familia BL/Ł/G/Π.^[60]​^[61]​

• Łukasiewicz, J. (1910). O zasadzie sprzeczności u Arystotelesa [Sobre el principio de contradicción en Aristóteles]. Kraków: Akademia Umiejętności.
• Łukasiewicz, J. (1910). O zasadzie wyłączonego środka [Sobre el principio del tercero excluido]. Przegląd Filozoficzny, 13, 372–373.
• Łukasiewicz, J. (1920). O pojęciu możliwości [Sobre el concepto de posibilidad]. Ruch Filozoficzny, 5, 169–170.
• Łukasiewicz, J. (1920). O logice trójwartościowej [Sobre la lógica trivalente]. Ruch Filozoficzny, 5, 170–171.
• Łukasiewicz, J. (1921). Logika dwuwartościowa [Lógica bivalente]. Przegląd Filozoficzny, 23, 189–205.
• Łukasiewicz, J. (1922/1923). Interpretacja liczbowa teorii zdań [Una interpretación numérica de la teoría de las proposiciones]. Ruch Filozoficzny, 7, 92–93.
• Łukasiewicz, J. (1929). Elementy logiki matematycznej. Warsaw: Wydawnictwo Koła Matematyczno-Fizycznego Słuchaczów UW. (2.ª ed. 1958; trad. ingl. Elements of Mathematical Logic. Oxford: Pergamon, 1966).
• Łukasiewicz, J., & Tarski, A. (1930). Untersuchungen über den Aussagenkalkül [Investigaciones sobre el cálculo sentencial]. Comptes Rendus de la Société des Sciences et des Lettres de Varsovie (Classe III), 23, 1–21.
• Łukasiewicz, J. (1930). Philosophische Bemerkungen zu mehrwertigen Systemen des Aussagenkalküls [Observaciones filosóficas sobre los sistemas polivalentes de la lógica proposicional]. Comptes Rendus de la Société des Sciences et des Lettres de Varsovie (Classe III), 23, 51–77.
• Łukasiewicz, J. (1931). Ein Vollständigkeitsbeweis des zweiwertigen Aussagenkalküls [Una prueba de completitud para el cálculo sentencial bivalente]. Comptes Rendus de la Société des Sciences et des Lettres de Varsovie (Classe III), 24, 153–183.
• Łukasiewicz, J. (1934). Z historii logiki zdań [Sobre la historia de la lógica de las proposiciones]. Przegląd Filozoficzny, 37, 417–437.
• Łukasiewicz, J. (1936). Bedeutung der logischen Analyse für die Erkenntnis [La importancia del análisis lógico para la cognición]. En Actes du VIIIe Congrès International de Philosophie (pp. 75–84). Prague.
• Łukasiewicz, J. (1937). W obronie logistyki [En defensa de la logística]. Studia Gnesnensia, 15, 12–26.
• Łukasiewicz, J. (1939). Der Äquivalenzkalkül [El cálculo equivalencial]. Collectanea Logica, 1, 145–169. (Texto original no publicado entonces; traducido en Selected Works, pp. 250–277).
• Łukasiewicz, J. (1941). Die Logik und das Grundlagenproblem [La lógica y el problema de los fundamentos]. En Les entretiens de Zurich sur les fondements et la méthode des sciences mathématiques (pp. 82–100). Zürich: Leemann Frères.
• Łukasiewicz, J. (1948). The shortest axiom of the implicational calculus of propositions. Proceedings of the Royal Irish Academy, Section A, 52, 25–33.
• Łukasiewicz, J. (1950). W sprawie aksjomatyki implikacyjnego rachunku zdań [Sobre el sistema de axiomas del cálculo proposicional implicacional]. Annales de la Société Polonaise de Mathématique, 22, 87–92.
• Łukasiewicz, J. (1951). On variable functors of propositional arguments. Proceedings of the Royal Irish Academy, Section A, 54, 25–35.
• Łukasiewicz, J. (1952). On the intuitionistic theory of deduction. Indagationes Mathematicae / Koninklijke Nederlandse Akademie van Wetenschappen, Proceedings Series A, 14, 201–212.
• Łukasiewicz, J. (1953). Sur la formalisation des théories mathématiques [Sobre la formalización de las teorías matemáticas]. En Colloques internationaux du Centre National de la Recherche Scientifique, 36: Les méthodes formelles en axiomatique (pp. 11–19). Paris: CNRS.
• Łukasiewicz, J. (1953). A system of modal logic. The Journal of Computing Systems, 1, 111–149. (Reimpreso en Selected Works, pp. 352–390).
• Łukasiewicz, J. (1954). Arithmetic and modal logic. The Journal of Computing Systems, 1, 213–219. (Reimpreso en Selected Works, pp. 391–400).
• Łukasiewicz, J. (1954). On a controversial problem of Aristotle’s modal syllogistic. Dominican Studies, 7, 114–128.
• Łukasiewicz, J. (1961). O determinizmie [Sobre el determinismo]. En J. Słupecki (Ed.), Z zagadnień logiki i filozofii. Pisma wybrane (pp. 114–126). Warsaw: PWN. (Trad. ingl. en Selected Works, pp. 110–128).
• Łukasiewicz, J. (1951). Aristotle’s syllogistic from the standpoint of modern formal logic (1.ª ed.). Oxford: Clarendon Press. (2.ª ed. amp., 1957).
• Łukasiewicz, J. (1970). Selected Works (L. Borkowski, Ed.). Amsterdam: North-Holland; Warsaw: PWN. (Recopilación de trabajos 1903–1958).

• Łukasiewicz, J. (1975). Estudios de lógica y filosofía (A. Deaño, sel., trad. y pról.). Revista de Occidente.
• Łukasiewicz, J. (1977). Para una historia de la lógica de enunciados (J. Sanmartín Esplugues, intr. y trad.). Universidad de Valencia (Cuadernos Teorema, 3). (Obra original publicada en 1929). Reimpresión/2.ª ed. en 1977.
• Łukasiewicz, J. (1977). La silogística de Aristóteles: desde el punto de vista de la lógica formal moderna (J. Fernández Robles, trad.; M. Garrido, rev. de la trad.; trad. de la 2.ª ed.). Tecnos. (Obra original publicada en 1951; 2.ª ed. revisada, 1957).
• Łukasiewicz, J. (2015). Sobre el principio de contradicción en Aristóteles (A. G. Vigo, pról.). Ediciones Encuentro (Opuscula Philosophica, 55).

• Notación polaca
• Alfred Tarski
• Escuela de Leópolis-Varsovia

• Entrada de Jan Łukasiewicz en la Stanford Encyclopedia of Philosophy