Grupo de homología persistente

En la homología persistente, un grupo de homología persistente es un análogo multiescala de un grupo de homología que captura información sobre la evolución de la características topológicas a través de una filtración de espacios. Mientras que el grupo de homología ordinario representa clases de homología no triviales de un espacio topológico individual, el grupo de homología persistente rastrea solo aquellas clases que siguen siendo no triviales a través de múltiples parámetros en la filtración subyacente. De manera análoga al número de Betti ordinario, los rangos de los grupos de homología persistente se conocen como números de Betti persistentes. Los grupos de homología persistente fueron introducidos por primera vez por Herbert Edelsbrunner, David Letscher y Afra Zomorodian en un artículo de 2002 Topological Persistence and Simplification, uno de los artículos fundamentales en los campos de la homología persistente y el análisis de datos topológicos, ^[1]​ basado en gran medida en los códigos de barras persistente y el algoritmo de persistencia, que fueron descritos por primera vez por Serguei Barannikov en el artículo de 1994. ^[2]​ Desde entonces, el estudio de los grupos de homología persistente ha dado lugar a aplicaciones en ciencia de datos, ^[3]​ aprendizaje automático, ^[4]​ ciencia de los materiales, ^[5]​ biología, ^[6]​ ^[7]​ y economía. ^[8]​

Dejar ${\displaystyle K}$ sea un complejo simplicial, y sea ${\displaystyle f:K\to \mathbb {R} }$ sea una función monótona de valor real. Entonces, para algunos valores ${\displaystyle a_{0}<a_{1}<\cdots <a_{n}\in \mathbb {R} }$ los conjuntos de subniveles ${\displaystyle K(a):=f^{-1}(-\infty ,a]}$ producir una secuencia de subcomplejos anidados ${\displaystyle \emptyset =K_{0}\subseteq K_{1}\subseteq \cdots \subseteq K_{n}=K}$ conocido como filtración de ${\displaystyle K}$.

Aplicando ${\displaystyle p^{th}}$ La homología con cada complejo produce una secuencia de grupos de homología. ${\displaystyle 0=H_{p}(K_{0})\to H_{p}(K_{1})\to \cdots \to H_{p}(K_{n})=H_{p}(K)}$ conectados por homomorfismos inducidos por los mapas de inclusión de la filtración subyacente. Cuando se toma la homología sobre un campo, obtenemos una secuencia de espacios vectoriales y mapas lineales conocida como módulo de persistencia.

Dejar ${\displaystyle f_{p}^{i,j}:H_{p}(K_{i})\to H_{p}(K_{j})}$ sea el homomorfismo inducido por la inclusión ${\displaystyle K_{i}\hookrightarrow K_{j}}$. Entonces el ${\displaystyle p^{th}}$ Los grupos de homología persistente se definen como las imágenes ${\displaystyle H_{p}^{i,j}:=\operatorname {im} f_{p}^{i,j}}$ a pesar de ${\displaystyle 1\leq i\leq j\leq n}$. En particular, el grupo de homología persistente ${\displaystyle H_{p}^{i,i}=H_{p}(K_{i})}$.

Más precisamente, la ${\displaystyle p^{th}}$ El grupo de homología persistente se puede definir como ${\displaystyle H_{p}^{i,j}=Z_{p}(K_{i})/\left(B_{p}(K_{j})\cap Z_{p}(K_{i})\right)}$, dónde ${\displaystyle Z_{p}(K_{\bullet })}$ y ${\displaystyle B_{p}(K_{\bullet })}$ son los grupos estándar de ciclo p y de límite p, respectivamente. ^[9]​

A veces los elementos de ${\displaystyle H_{p}^{i,j}}$ se describen como las clases de homología que "nacen" en o antes ${\displaystyle K_{i}}$ y que aún no han "muerto" entrando ${\displaystyle K_{j}}$ . Estas nociones pueden precisarse de la siguiente manera: Una clase de homología ${\displaystyle \gamma \in H_{p}(K_{i})}$ Se dice que nació en ${\displaystyle K_{i}}$ si no está contenido en la imagen del grupo de homología persistente anterior, es decir, ${\displaystyle \gamma \notin H_{p}^{i-1,i}}$ . En cambio, ${\displaystyle \gamma }$ Se dice que muere entrando ${\displaystyle K_{j}}$ si ${\displaystyle \gamma }$ se subsume (es decir, se fusiona con) otra clase más antigua a medida que la secuencia procede desde ${\displaystyle K_{j-1}\to K_{j}}$. Es decir, ${\displaystyle f_{p}^{i,j-1}(\gamma )\notin H_{p}^{i-1,j-1}}$ pero ${\displaystyle f_{p}^{i,j}(\gamma )\in H_{p}^{i-1,j}}$ . La determinación de que una clase más antigua persiste si se fusiona con una clase más joven, en lugar de lo contrario, a veces se conoce como la Regla de los Ancianos. ^[10]​ ^[11]​

Los índices ${\displaystyle i,j}$ en el que una clase de homología ${\displaystyle \gamma }$ nace y muere entrando se conocen como índices de nacimiento y muerte de ${\displaystyle \gamma }$. La diferencia ${\displaystyle j-i}$ se conoce como el índice de persistencia de ${\displaystyle \gamma }$, mientras que la diferencia correspondiente ${\displaystyle a_{j}-a_{i}}$ En función de los valores correspondientes a esos índices se conoce como persistencia de ${\displaystyle \gamma }$. Si no existe ningún índice en el que ${\displaystyle \gamma }$ muere, se le asigna un índice de muerte infinito. Así, la persistencia de cada clase se puede representar como un intervalo en la línea real extendida. ${\displaystyle \mathbb {R} \cup \{\pm \infty \}}$ de cualquiera de las formas ${\displaystyle [a_{i},a_{j})}$ o ${\displaystyle [a_{i}',\infty )}$. Dado que, en el caso de un campo infinito, el número infinito de clases siempre tiene la misma persistencia, la colección de todas las clases de dichos intervalos no da multiplicidades significativas para un multiconjunto de intervalos. En cambio, tales multiplicidades y un multiconjunto de intervalos en la línea real extendida están dados por el teorema de estructura de homología de persistencia. ^[2]​ Este conjunto múltiple se conoce como código de barras de persistencia. ^[12]​

Concretamente, el teorema de estructura establece que para cualquier complejo filtrado sobre un campo ${\displaystyle F}$, existe una transformación lineal que preserva la filtración y convierte el complejo filtrado en la llamada forma canónica, una suma directa definida canónicamente de complejos filtrados de dos tipos: complejos bidimensionales con homología trivial ${\displaystyle d(e_{a_{j}})=e_{a_{i}}}$ y complejos unidimensionales con diferenciales triviales ${\displaystyle d(e_{a'_{i}})=0}$. ^[2]​

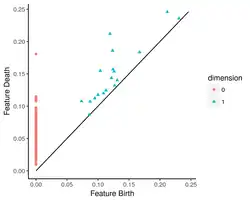
Geométricamente, un código de barras se puede trazar como un conjunto múltiple de puntos (con coordenadas posiblemente infinitas) ${\displaystyle (a_{i},a_{j})}$ en el plano extendido ${\displaystyle \left(\mathbb {R} \cup \{\pm \infty \}\right)^{2}}$. Según las definiciones anteriores, cada punto estará por encima de la diagonal, y la distancia a la diagonal es exactamente igual a la persistencia de los tiempos de clase correspondientes ${\displaystyle {\frac {1}{\sqrt {2}}}}$. Esta construcción se conoce como diagrama de persistencia y proporciona una forma de visualizar la estructura de la persistencia de las clases de homología en la secuencia de grupos de homología persistentes. ^[1]​