Traslación de ejes

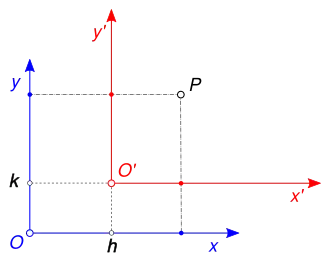
En matemáticas, una traslación de ejes en dos dimensiones es una corrspondencia entre un sistema de coordenadas cartesianas xy y un sistema de coordenadas cartesianas x'y', en el que el eje x' es paralelo respecto al eje x y está a k unidades de distancia, y el eje y' es paralelo al eje y y está a h unidades de distancia. Esto significa que el origen O' del nuevo sistema de coordenadas tiene coordenadas (h, k) en el sistema original. Las direcciones positivas x' e y' se consideran iguales a las direcciones positivas x e y. Un punto P tiene coordenadas (x, y) con respecto al sistema original y coordenadas (x', y') con respecto al nuevo sistema, donde:^[1]​^[2]​

o equivalentemente

En el nuevo sistema de coordenadas, el punto P parecerá haber sido trasladado en la dirección opuesta. Por ejemplo, si el sistema xy se traslada una distancia h a la derecha y una distancia k hacia arriba, entonces P parecerá haber sido trasladado una distancia h a la izquierda y una distancia k hacia abajo en el sistema x'y'. Una traslación de ejes en más de dos dimensiones se define de forma similar.^[3]​ Una traslación de ejes es una transformación rígida, pero no un aplicación lineal (véase homología afín).

Los sistemas de coordenadas son esenciales para estudiar las ecuaciones de las curvas empleando los métodos de la geometría analítica. Para utilizar el método de la geometría de coordenadas, los ejes se colocan en una posición conveniente con respecto a la curva en cuestión. Por ejemplo, para estudiar las ecuaciones de elipses e hipérbolas, los focos suelen ubicarse en uno de los ejes y se sitúan simétricamente con respecto al origen. Si la curva (hipérbola, parábola, elipse u otra) no está situada convenientemente con respecto a los ejes, se debe cambiar el sistema de coordenadas para colocar la curva en una ubicación y orientación más favorables. El proceso de realizar este cambio se denomina transformación de coordenadas.^[4]​

Las soluciones a muchos problemas se pueden simplificar trasladando los ejes de coordenadas para obtener nuevos ejes paralelos a los originales.^[1]​

Mediante un cambio de coordenadas, la ecuación de una sección cónica se puede convertir en una forma estándar, que suele ser más fácil de manejar. Para la ecuación más general de segundo grado, que toma la forma:

siempre es posible realizar una rotación de ejes de tal manera que en el nuevo sistema la ecuación tome la forma:

es decir, eliminando el término xy.^[5]​ En consecuencia, una traslación de ejes puede reducir una ecuación de la forma (3) a una ecuación de la misma forma, pero con nuevas variables (x', y') como coordenadas, y con los valores de D y de E ambos iguales a cero (con ciertas excepciones, por ejemplo, en las parábolas). La herramienta principal en este proceso es completar el cuadrado.^[6]​ En los ejemplos que siguen, se asume que ya se ha realizado una rotación de ejes.

Dada la ecuación:

${\displaystyle 9x^{2}+25y^{2}+18x-100y-116=0,}$

mediante una traslación de ejes, determínese si el lugar geométrico de la ecuación es una parábola, una elipse o una hipérbola. Determinar sus focos, vértices (o vértice) y excentricidad.

Solución: Para completar el cuadrado en x e y, escribir la ecuación en la forma:

${\displaystyle 9(x^{2}+2x)+25(y^{2}-4y)=116.}$

Completar los cuadrados y obtener

${\displaystyle 9(x^{2}+2x+1)+25(y^{2}-4y+4)=116+9+100}$

${\displaystyle \Leftrightarrow 9(x+1)^{2}+25(y-2)^{2}=225.}$

Definir

${\displaystyle x'=x+1}$      e      ${\displaystyle y'=y-2.}$

Es decir, la traslación en las ecuaciones (2) se realiza con ${\displaystyle h=-1,k=2.}$ La ecuación en el nuevo sistema de coordenadas toma la forma

Dividir la ecuación (5) entre 225 para obtener

${\displaystyle {\frac {x'^{2}}{25}}+{\frac {y'^{2}}{9}}=1,}$

que se reconoce como una elipse con ${\displaystyle a=5,b=3,c^{2}=a^{2}-b^{2}=16,c=4,e={\tfrac {4}{5}}.}$ En el sistema x'y', se tiene que: centro ${\displaystyle (0,0)}$; vértices ${\displaystyle (\pm 5,0)}$; y focos ${\displaystyle (\pm 4,0).}$

En el sistema xy, usar las relaciones ${\displaystyle x=x'-1,y=y'+2}$ para obtener: centro ${\displaystyle (-1,2)}$; vértices ${\displaystyle (4,2),(-6,2)}$; focos ${\displaystyle (3,2),(-5,2)}$; y excentricidad ${\displaystyle {\tfrac {4}{5}}.}$^[7]​

Para un sistema de coordenadas cartesianas xyz en tres dimensiones, supóngase que se introduce un segundo sistema de coordenadas cartesianas, con los ejes x', y' y z' ubicados de forma que el eje x' sea paralelo al eje x y esté a h unidades de este, el eje y' sea paralelo al eje y y esté a k unidades de este, y el eje z' sea paralelo al eje z y esté a l unidades de este. Un punto P en el espacio tendrá coordenadas en ambos sistemas. Si sus coordenadas son (x, y, z) en el sistema original y (x', y', z') en el segundo sistema, se cumplen las ecuaciones

Las ecuaciones^[8]​ (6) definen una traslación de ejes en tres dimensiones, donde (h, k, l) son las coordenadas xyz del nuevo origen.^[1]​ Una traslación de ejes en cualquier número finito de dimensiones se define de forma similar.

En el espacio tridimensional, la ecuación más general de segundo grado en x, y y z tiene la forma

donde las cantidades ${\displaystyle A,B,C,\ldots ,J}$ son números positivos, negativos o cero. Todos los puntos en el espacio que satisfacen dicha ecuación se encuentran en una superficie. Cualquier ecuación de segundo grado que no se reduce a un cilindro, un plano, una línea recta o un punto, corresponde a una superficie llamada cuadrática.^[9]​

Al igual que en el caso de la geometría analítica plana, el método de traslación de ejes puede utilizarse para simplificar ecuaciones de segundo grado, evidenciando así la naturaleza de ciertas superficies cuadráticas. La herramienta principal en este proceso es completar el cuadrado.^[10]​

Utilizar una traslación de coordenadas para identificar la superficie cuadrática.

${\displaystyle x^{2}+4y^{2}+3z^{2}+2x-8y+9z=10.}$

Solución: Escribir la ecuación en la forma:

${\displaystyle x^{2}+2x+4(y^{2}-2y)+3(z^{2}+3z)=10.}$

Completar el cuadrado para obtener:

${\displaystyle (x+1)^{2}+4(y-1)^{2}+3(z+{\tfrac {3}{2}})^{2}=10+1+4+{\tfrac {27}{4}}.}$

Introducir la traslación de coordenadas:

${\displaystyle x'=x+1,\qquad y'=y-1,\qquad z'=z+{\tfrac {3}{2}}.}$

La ecuación de la superficie toma la forma:

${\displaystyle x'^{2}+4y'^{2}+3z'^{2}={\tfrac {87}{4}},}$

que se reconoce como la ecuación de un elipsoide.^[10]​

• Cambio de base
• Traslación

• Anton, Howard (1987), Elementary Linear Algebra (5th edición), New York: Wiley, ISBN 0-471-84819-0 .
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd edición), Reading: Addison-Wesley, LCCN 76087042 .