Sucesión loxodrómica de circunferencias tangentes de Coxeter

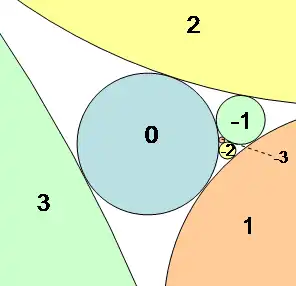
En geometría, la sucesión loxodrómica de circunferencias tangentes de Coxeter es una sucesión infinita de circunferencias dispuestas de modo que cuatro circunferencias consecutivas cualesquiera en la sucesión son tangentes entre sí por pares. Esto significa que cada circunferencia de la sucesión es tangente a las tres circunferencias que la preceden y también a las tres circunferencias que la siguen.

Los radios de los circunferencias de la sucesión forman una progresión geométrica con razón:

$${\displaystyle k=\varphi +{\sqrt {\varphi }}\approx 2.89005\ ,}$$

donde ${\displaystyle \varphi }$ es el número áureo. Esta razón ${\displaystyle k}$ y su recíproco satisfacen la ecuación

$${\displaystyle (1+x+x^{2}+x^{3})^{2}=2(1+x^{2}+x^{4}+x^{6})\ ,}$$

y, por lo tanto, cuatro circunferencias consecutivas cualesquiera en la sucesión cumplen las condiciones del teorema de las circunferencias de Descartes.^[1]​^[2]​

Los centros de los circunferencias de la sucesión se encuentran en una espiral logarítmica. Visto desde el centro de la espiral, el ángulo entre los centros de circunferencias sucesivos es:^[1]​

$${\displaystyle \cos ^{-1}\left({\frac {-1}{\varphi }}\right)\approx 128.173^{\circ }\ .}$$

El ángulo entre ternas consecutivas de centros es:

$${\displaystyle \theta =\cos ^{-1}{\frac {1}{\varphi }}\approx 51.8273^{\circ },}$$

igual que uno de los ángulos del triángulo de Kepler, un triángulo rectángulo cuya construcción también implica la raíz cuadrada de la proporción áurea.^[3]​

La construcción recibe su nombre del geómetra H. S. M. Coxeter, quien generalizó el caso bidimensional a sucesiones de esferas y de n-esferas en dimensiones superiores.^[1]​^[4]​^[5]​ Puede interpretarse como un caso especial degenerado de la espiral de Doyle.^[2]​

• Tamiz de Apolonio

• Weisstein, Eric W. «Coxeter's Loxodromic Sequence of Tangent Circles». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.