Espiral de Doyle

En las matemáticas del empaquetamiento de circunferencias, una espiral de Doyle es un patrón de circunferencias que no se cruzan en el plano, y donde cada una está rodeada por un anillo de otras seis circunferencias tangentes. Estos patrones contienen brazos espirales formados por circunferencias con puntos de tangencia opuestos, con sus centros alineados en una espiral logarítmica de tres formas diferentes.

Las espirales de Doyle reciben su nombre del matemático Peter G. Doyle, quien hizo una importante contribución a su construcción matemática a finales de la década de 1980 o al principio de los años 1990.^[2]​ Sin embargo, su estudio sobre la filotaxis (las matemáticas del crecimiento de las plantas) se remonta a principios de los años 1900.^[1]​^[3]​^[4]​

Una espiral de Doyle se define como un tipo de empaquetamiento de circunferencias, compuesto por un número infinito de circunferencias en el plano, sin ningún par de circunferencias con interiores superpuestos. En una espiral de Doyle, cada circunferencia está rodeada por un anillo de otras seis circunferencias, que son tangentes a la circunferencia central y a sus dos circunferencias vecinas en el anillo.^[5]​^[6]​

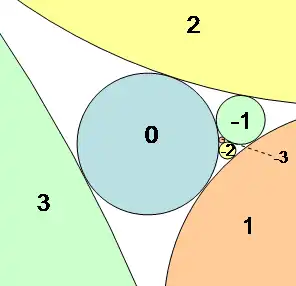
Como observó Doyle,^[2]​ la única manera de empaquetar circunferencias con la estructura combinatoria de una espiral de Doyle es usar circunferencias con radios de valores altamente estructurados.structured.^[5]​ Se pueden empaquetar seis circunferencias alrededor de una circunferencia de radio ${\displaystyle r}$ si y solo si existen tres números reales positivos ${\displaystyle a}$, ${\displaystyle b}$, y ${\displaystyle c={\tfrac {b}{a}}}$, tales que las circunferencias circundantes tengan radios (en orden cíclico):

${\displaystyle ra}$, ${\displaystyle rb}$, ${\displaystyle rc}$, ${\displaystyle r/a}$, ${\displaystyle r/b}$, y ${\displaystyle r/c}$.

Solo ciertas ternas de números ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c={\tfrac {b}{a}}}$ provienen de espirales de Doyle; otras corresponden a sistemas de circunferencias que finalmente se superponen con otra.^[6]​^[7]​

En una espiral de Doyle, se pueden agrupar las circunferencias en cadenas que se conectan a través de puntos de tangencia opuestos. Estos grupos se han denominado "brazos", siguiendo la misma terminología utilizada para las galaxias espirales.^[9]​^[10]​ Dentro de cada brazo, las circunferencias tienen radios en una progresión geométrica doblemente infinita:

$${\displaystyle \dots ,ra^{-2},ra^{-1},r,ra,ra^{2},\dots }$$

o una secuencia del mismo tipo con un multiplicador común ${\displaystyle b}$ o ${\displaystyle c}$. En la mayoría de las espirales de Doyle, los centros de las circunferencias en un solo brazo se encuentran en una espiral logarítmica, y todas las espirales logarítmicas obtenidas de esta manera se unen en un único punto central. Algunas espirales de Doyle, en cambio, tienen brazos circulares concéntricos (como en la vidriera mostrada) o brazos rectos.^[6]​

La forma precisa de cualquier espiral de Doyle se puede parametrizar mediante tres números naturales, contando el número de brazos de cada una de sus tres formas. Cuando una forma de brazo se presenta con frecuencia infinita, su conteo se define como 0, en lugar de ${\displaystyle \infty }$. El conteo de brazos más pequeño es igual a la diferencia de los otros dos conteos de brazos, por lo que cualquier espiral de Doyle puede describirse como de tipo ${\displaystyle (p,q)}$, donde ${\displaystyle p}$ y ${\displaystyle q}$ son los dos conteos más grandes, en el orden ordenado ${\displaystyle p\leq q}$.^[11]​

2 brazos

6 brazos

8 brazos

Contando los brazos de cada tipo en una espiral de tipo (6,8)

Cada par ${\displaystyle (p,q)}$ con ${\displaystyle 1<q/2\leq p\leq q}$ determina una espiral de Doyle, con su tercer y más pequeño conteo de brazos igual a ${\displaystyle q-p}$. La forma de esta espiral está determinada únicamente por estos conteos, prescindiendo de semejanzas.^[5]​ Para una espiral de tipo ${\displaystyle (p,q)}$, los multiplicadores de radio son ${\displaystyle a=|\alpha |}$, ${\displaystyle b=|\beta |}$, and ${\displaystyle c={\tfrac {b}{a}}}$ para dos números complejos ${\displaystyle \alpha }$ y ${\displaystyle \beta }$ que satisfacen la ecuación de coherencia ${\displaystyle \alpha ^{p}=\beta ^{q}}$ y las ecuaciones de tangencia:

${\displaystyle {\frac {1+|\alpha |}{|1-\alpha |}}={\frac {1+|\beta |}{|1-\beta |}}={\frac {|\alpha |+|\beta |}{|\alpha -\beta |}}.}$

Esto implica que los multiplicadores de radio son números algebraicos.^[9]​^[7]​ Las autosimilitudes de una espiral centrada en el origen forman un grupo discreto generado por ${\displaystyle z\mapsto \alpha z}$ y ${\displaystyle z\mapsto \beta z}$.^[7]​ Una circunferencia cuyo centro está a una distancia ${\displaystyle d}$ del punto central de la espiral tiene un radio ${\displaystyle {\tfrac {|1-\alpha |}{1+|\alpha |}}d}$.^[9]​

Se conocen los valores exactos de estos parámetros para algunos casos sencillos. En otros casos, se pueden aproximar con precisión mediante una búsqueda numérica, cuyos resultados se pueden utilizar para determinar valores numéricos para los tamaños y posiciones de todas las circunferencias.^[5]​^[9]​

Las espirales de Doyle presentan simetrías que combinan escalado y rotación alrededor del punto central (o traslación y rotación, en el caso del empaquetamiento hexagonal regular del plano mediante circunferencias unidad), convirtiendo cualquier circunferencia del empaquetamiento en cualquier otra.^[6]​ La aplicación de una transformación de Möbius a una espiral de Doyle conserva la forma y las tangencias de sus circunferencias. Por lo tanto, una transformación de Möbius puede producir patrones adicionales de circunferencias tangentes que no se cruzan, cada una tangente a otras seis. Estos patrones suelen tener un patrón de doble espiral en el que las secuencias conectadas de circunferencias se despliegan en espiral desde un punto central (la imagen del centro de la espiral de Doyle) hacia otro punto (la imagen del punto del infinito). Sin embargo, estos conjuntos no cumplen todos los requisitos de las espirales de Doyle: algunas circunferencias en este patrón no estarán rodeadas por otras seis circunferencias vecinas.^[9]​^[12]​

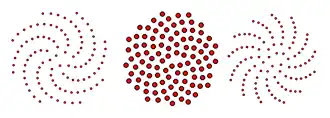
El caso más general de una espiral de Doyle tiene tres multiplicadores de radio todos distintos de 1, diferentes, y tres brazos distintos, todos distintos de cero. Un ejemplo es la sucesión loxodrómica de circunferencias tangentes de Coxeter, una espiral de Doyle de tipo (2,3), con brazos 1, 2 y 3, y con multiplicadores ${\displaystyle \alpha =\tau ^{3}}$ y ${\displaystyle \beta =\tau ^{2}}$ para

${\displaystyle \tau =-(1+{\frac {1}{\sqrt {\varphi }}})+i(1+{\sqrt {\varphi }}),}$

donde ${\displaystyle \varphi }$ denota el número áureo. Dentro del brazo espiral único de curvatura más cerrada, los círculos en la secuencia loxodrómica de Coxeter forman una secuencia cuyos radios son potencias de ${\displaystyle |\tau |=\varphi +{\sqrt {\varphi }}}$. Cada cuatro circunferencias consecutivas en esta secuencia son tangentes.^[12]​

Cuando exactamente uno de los conteos de los tres brazos es cero, los brazos que se cuentan son circulares, con radios múltiplos de 1. El número de circunferencias en cada uno de estos brazos circulares es igual al número de brazos de cada uno de los otros dos tipos. Todos los brazos circulares son concéntricos, centrados donde los brazos espirales se encuentran.^[5]​ Los multiplicadores para una espiral de Doyle de tipo ${\displaystyle (p,p)}$ son ${\displaystyle \alpha =ae^{i{\frac {\pi }{p}}}}$ y ${\displaystyle \beta =ae^{-i{\frac {\pi }{p}}}}$.^[9]​^[13]​ En la foto de una vidriera de iglesia, los dos anillos de nueve círculos pertenecen a una espiral de Doyle de esta forma, del tipo (9,9).

Los brazos rectos se producen para los conteos de brazos que cumplen la relación ${\displaystyle p=q/2}$. En este caso, los dos tipos de brazos en espiral tienen el mismo multiplicador de radio y son reflejos especulares entre sí. Hay el doble de brazos rectos que espirales de cada tipo. Cada brazo recto está formado por circunferencias cuyos centros se encuentran en un rayo que pasa por el punto central.^[5]​ Dado que el número de brazos rectos debe ser par, estos pueden agruparse en pares opuestos, con los dos rayos de cada par uniéndose para formar una línea recta. Los multiplicadores para una espiral de Doyle del tipo ${\displaystyle (p,2p)}$ son ${\displaystyle \alpha =b^{2}}$ y ${\displaystyle \beta =be^{i{\frac {\pi }{p}}}}$.^[9]​^[14]​ La espiral de Doyle de tipo (8,16) de la ilustración de "Popular Science" es un ejemplo, con ocho brazos que giran en la misma dirección que el brazo sombreado, otros ocho brazos reflejados y dieciséis rayos.

Un último caso especial es la espiral de Doyle de tipo (0,0), un empaquetamiento hexagonal regular del plano mediante circunferencias unitarias. Sus multiplicadores de radio son todos uno y sus brazos forman familias paralelas de líneas de tres pendientes diferentes.^[5]​

Las espirales de Doyle forman un análogo discreto de la función exponencial, como parte del uso más general de los empaquetamientos de circunferencias como análogos discretos de las transformaciones conformes. De hecho, se pueden obtener patrones muy similares a las espirales de Doyle (pero construidas con formas tangentes que no son circunferencias) aplicando la función exponencial a una copia a escala del patrón de empaquetamiento hexagonal regular de circunferencias.^[5]​ Las tres razones de los radios entre círculos adyacentes, fijas en la espiral, pueden considerarse análogas a una caracterización de la función exponencial con valores fijos de la derivada schwarziana.^[6]​ Las espirales de Doyle se han utilizado para estudiar los grupos kleinianos, grupos discretos de simetrías del espacio hiperbólico, incrustando estas espirales en la esfera en el infinito del espacio hiperbólico y elevando las simetrías de cada espiral a las simetrías del propio espacio.^[9]​

Se han utilizado espirales de circunferenciass tangentes, a menudo con números de brazos tomados de la sucesión de Fibonacci, para modelar la filotaxis, los patrones de crecimiento en espiral característicos de ciertas especies de plantas, comenzando con el trabajo de Gerrit van Iterson en 1907.^[4]​ En este contexto, un brazo de la espiral de Doyle se denomina parastiquio y los conteos de brazos de la espiral de Doyle se denominan "números parastíquicos". Cuando los dos números parastíquicos ${\displaystyle p}$ y ${\displaystyle q}$ pertenecen a la sucesión de Fibonacci, y son consecutivos o separados por un solo número de Fibonacci, entonces el tercer número parastíquico también será un número de Fibonacci.^[15]​ Con esta aplicación en mente, Arnold Emch en 1910 calculó las posiciones de las circunferencias en espirales de Doyle de tipo ${\displaystyle (p,2p)}$, mostrando en su trabajo las conexiones entre estas espirales, las espirales logarítmicas y la función exponencial.^[1]​^[3]​ Para modelar el crecimiento de las plantas de esta manera, también pueden usarse empaquetamientos espirales de circunferencias tangentes en superficies distintas del plano, incluyendo cilindros y conos.^[16]​

Los empaquetamientos espirales de circunferencias también se han estudiado como motivo decorativo en arquitectura.^[8]​

Las circunferencias tangentes pueden formar patrones espirales cuya estructura local se asemeja a una cuadrícula en lugar de una red hexagonal, que puede transformarse continuamente en empaquetamientos de Doyle.^[15]​ El espacio de empaquetamientos espirales localmente cuadrados es de dimensión infinita, a diferencia de las espirales de Doyle, que pueden determinarse mediante un número constante de parámetros.^[17]​ También es posible describir sistemas espirales de circunferencias superpuestas que recubren el plano, en lugar de circunferencias no cruzadas que se empaquetan en él, con cada punto del plano cubierto por un máximo de dos circunferencias, excepto los puntos donde tres circunferencias se encuentran en ángulos de ${\displaystyle 60^{\circ }}$, y con cada circunferencia rodeada por otras seis. Estos disposiciones comparten muchas propiedades con la espiral de Doyle.^[18]​

La espiral de Doyle no debe confundirse con un patrón espiral diferente de circunferencias, estudiado para ciertas formas de crecimiento vegetal, como las semillas de girasol. En este patrón, las circunferencias tienen un tamaño unitario en lugar de crecer logarítmicamente, y no son tangentes entre sí. En lugar de tener los centros situados en una espiral logarítmica, se ubican en una espiral de Fermat, separados entre sí por el ángulo áureo ${\displaystyle 2\pi /\varphi ^{2}\approx 137.5^{\circ }.}$ con respecto al centro de la espiral, donde ${\displaystyle \varphi }$ es el número áureo.^[19]​^[20]​

• Yamagishi, Yoshikazu; Sushida, Takamichi (mes de abril de 2017), «Spiral disk packings», Physica D: Nonlinear Phenomena 345: 1-10, Bibcode:2017PhyD..345....1Y, doi:10.1016/j.physd.2016.12.003 .

• Doyle spiral explorer, Robin Houston