Red eléctrica antimétrica

Una red eléctrica antimétrica es una red eléctrica que presenta propiedades eléctricas antisimétricas. El término se utiliza a menudo en la teoría de filtros, pero se aplica al análisis general de redes eléctricas. Antimétrica es el opuesto diametral de simétrica; no significa simplemente «asimétrica» (es decir, «carente de simetría»). Es posible que las redes sean simétricas o antimétricas en sus propiedades eléctricas sin ser física o topológicamente simétricas o antimétricas.

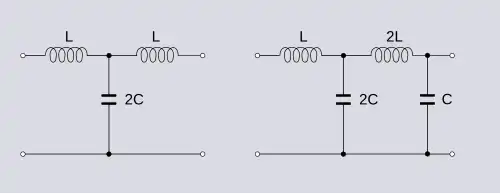
Las referencias a la simetría y antimetría de una red suelen referirse a las impedancias de entrada^{[nota 1]}​ de una red de dos puertos cuando está correctamente terminada.^{[nota 2]}​ Una red simétrica tendrá dos impedancias de entrada iguales, Z_i1 y Z_i2. Para una red antimétrica, las dos impedancias deben ser el dual de la otra con respecto a alguna impedancia nominal R₀. Es decir,^[1]​

${\displaystyle {\frac {Z_{i1}}{R_{0}}}={\frac {R_{0}}{Z_{i2}}}}$

o, de forma equivalente

${\displaystyle Z_{i1}Z_{i2}={R_{0}}^{2}.}$

Para la antimetría es necesario que las impedancias de terminación sean también el dual de la otra, pero en muchos casos prácticos las dos impedancias de terminación son resistencias y ambas son iguales a la impedancia nominal R₀. Por lo tanto, son simétricas y antimétricas al mismo tiempo.^[1]​

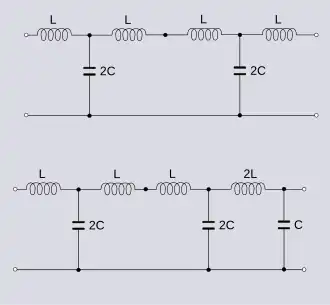
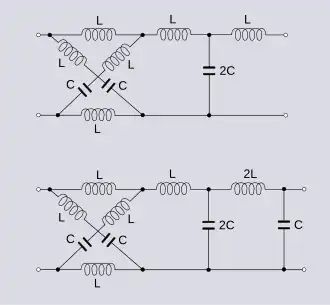
Las redes simétricas y antimétricas suelen ser también topológicamente simétricas y antimétricas, respectivamente. La disposición física de sus componentes y valores es simétrica o antimétrica, como en el ejemplo de la escalera anterior. Sin embargo, no es una condición necesaria para la antimetría eléctrica. Por ejemplo, si a las redes de ejemplo de la figura 1 se les añade una sección T idéntica adicional en el lado izquierdo, como se muestra en la figura 2, las redes siguen siendo topológicamente simétricas y antimétricas. Sin embargo, la red resultante de la aplicación del teorema de bisección de Bartlett^[2]​ aplicado a la primera sección en T de cada red, como se muestra en la figura 3, no es físicamente simétrica ni antimétrica, pero conserva sus propiedades eléctricas simétricas (en el primer caso) y antimétricas (en el segundo caso).^[3]​

Las condiciones de simetría y antimetría pueden establecerse en términos de parámetros de dos puertos. Para una red de dos puertos descrita mediante parámetros de impedancia normalizados (parámetros z),

${\displaystyle z_{11}=z_{22}}$

si la red es simétrica, y

${\displaystyle z_{11}z_{22}-z_{12}z_{21}=1}$

si la red es antimétrica. Las redes pasivas del tipo ilustrado en este artículo también son recíprocas, lo que requiere que

${\displaystyle z_{12}=z_{21}}$

y da como resultado una matriz de parámetros z normalizada de,

${\displaystyle \left[\mathbf {z} \right]={\begin{bmatrix}z_{11}&z_{12}\\z_{12}&z_{11}\end{bmatrix}}}$

para redes simétricas y

${\displaystyle \left[\mathbf {z} \right]={\begin{bmatrix}z_{11}&z_{12}\\z_{12}&(z_{12}^{2}+1)/z_{11}\end{bmatrix}}}$

para redes antimétricas.^[4]​

Para una red de dos puertos descrita mediante parámetros de dispersión (parámetros S),

${\displaystyle S_{11}=S_{22}}$

si la red es simétrica, y

${\displaystyle S_{11}=-S_{22}}$

si la red es antimétrica.^[5]​ La condición de reciprocidad es,

${\displaystyle S_{12}=S_{21}}$

resultando una matriz de parámetros S de,

${\displaystyle \left[\mathbf {S} \right]={\begin{bmatrix}S_{11}&S_{12}\\S_{12}&S_{11}\end{bmatrix}}}$

para redes simétricas y

${\displaystyle \left[\mathbf {S} \right]={\begin{bmatrix}S_{11}&S_{12}\\S_{12}&-S_{11}\end{bmatrix}}}$

para redes antimétricas.^[6]​

Algunos diseños de circuitos producen naturalmente redes antimétricas. Por ejemplo, un filtro Butterworth de paso bajo implementado como una red en escalera con un número par de elementos será antimétrico. Del mismo modo, un filtro Butterworth paso banda con un número par de resonadores será antimétrico, al igual que un filtro mecánico Butterworth con un número par de resonadores mecánicos.^[7]​