Poliedro de caras regulares

Un poliedro de caras regulares^[1]​ es un poliedro que cumple con que todas sus caras son polígonos regulares. En esta clase existe una variedad infinita de poliedros, e incluye tanto poliedros convexos como no convexos.

Existen varias subcategorías dentro de esta familia según las características en común que compartan los poliedros, pero estas no contienen a todos los poliedros de caras regulares que hay.

Los 5 sólidos platónicos o poliedros regulares, los cuales son convexos, isoedrales e isogonales:

Nombre	Imagen	Símbolo de Schläfli	Configuración de vértices
Tetraedro		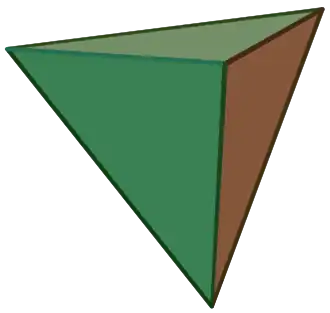{3,3}	3.3.3
Cubo o hexaedro regular		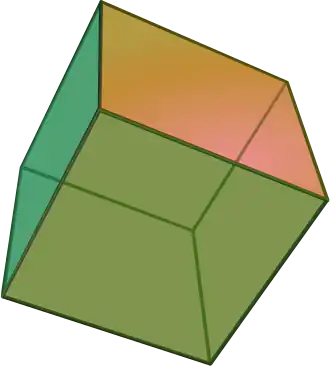{4,3}	4.4.4
Octaedro		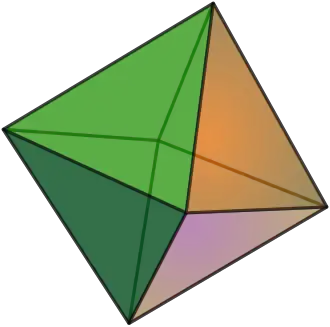{3,4}	3.3.3.3
Dodecaedro		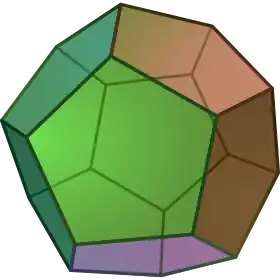{5,3}	5.5.5
Icosaedro		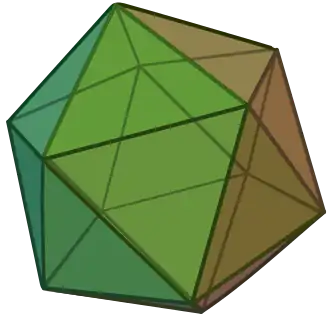{3,5}	3.3.3.3.3

Los 13 sólidos arquimedianos^[2]​ o sólidos de Arquímedes, los cuales son convexos e isogonales, pero no isoedrales, y no incluyen a las familias infinitas de los prismas y los antiprismas:

Nombre	Imagen	Configuración de vértices
Tetraedro truncado		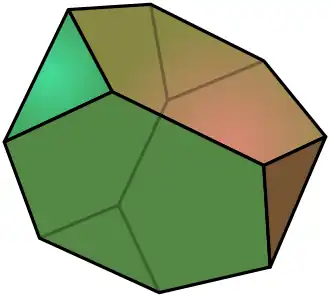3.6.6
Cuboctaedro		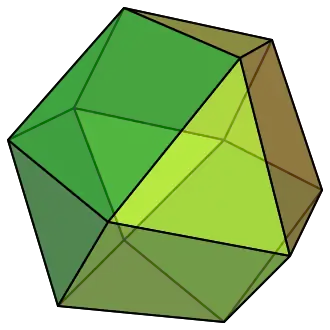3.4.3.4
Cubo truncado		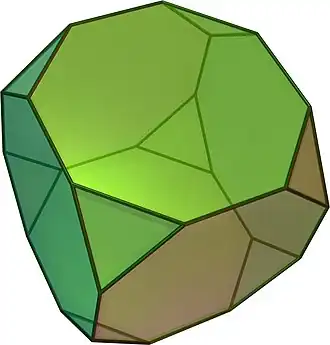3.8.8
Octaedro truncado		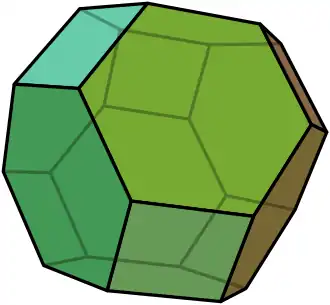4.6.6
Rombicuboctaedro		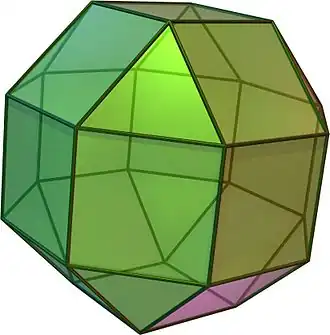3.4.4.4
Cuboctaedro truncado		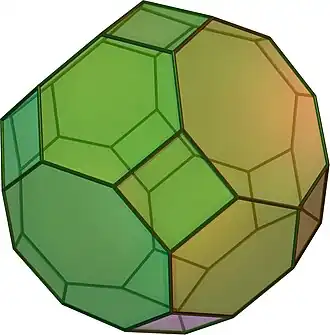4.6.8
Cubo romo		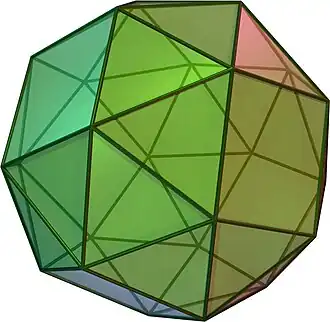3.3.3.3.4
Icosidodecaedro		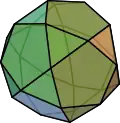3.5.3.5
Dodecaedro truncado		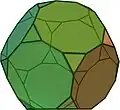3.10.10
Icosaedro truncado		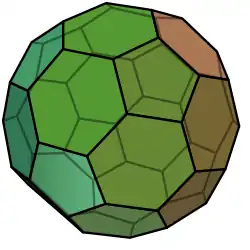5.6.6
Rombicosidodecaedro		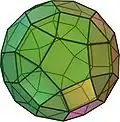3.4.5.4
Icosidodecaedro truncado		4.6.10
Dodecaedro romo		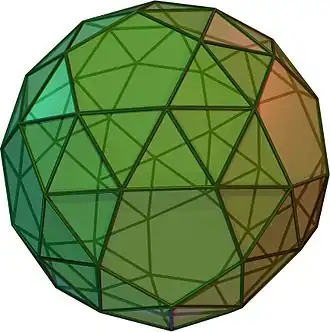3.3.3.3.5

Los únicos poliedros convexos uniformes que no pertenecen ni a los sólidos arquimedianos ni a los sólidos platónicos son los poliedros prismáticos no isoedrales:

• La familia infinita de los prismas (menos el prisma cuadrado)
• La familia infinita de los antiprismas (menos el antiprisma digonal y el antiprisma triangular)

Los 92 sólidos de Johnson son los únicos poliedros de caras regulares convexos no uniformes.

Los 4 sólidos de Kepler-Poinsot, los cuales son poliedros regulares estrellados:

Nombre	Imagen	Símbolo de Schläfli	Configuración de vértices
Gran dodecaedro		{5,5⁄2}	(55)/2
Pequeño dodecaedro estrellado		{5⁄2,5}	(5⁄2)5
Gran icosaedro		{3,5⁄2}	(35)/2
Gran dodecaedro estrellado		{5⁄2,3}	(5⁄2)3

• La familia infinita de los poliedros prismáticos estrellados, los cuales tienen polígonos estrellados como bases:
  • La familia infinita de los prismas de base estrellada
  • La familia infinita de los antiprismas de base estrellada
• Los 53 poliedros uniformes estrellados que no pertenecen ni a los sólidos de Kepler-Poinsot ni a los poliedros prismáticos estrellados

Los 3 teselados regulares, los cuales al poseer ángulos diedros de 180° se extienden infinitamente, teselando completamente el plano. No son convexos y son isoedrales e isogonales:

Nombre	Imagen	Símbolo de Schläfli	Configuración de vértices
Teselado triangular		{3,6}	3.3.3.3.3.3
Teselado cuadrado		{4,4}	4.4.4.4
Teselado hexagonal		{6,3}	6.6.6

Solo hay ocho teselados uniformes no regulares:

Nombre	Imagen	Configuración de vértices
Teselado cuadrado truncado		4.8.8
Teselado cuadrado romo		3.3.4.3.4
Teselado trihexagonal		3.6.3.6
Teselado hexagonal truncado		3.12.12
Teselado rombitrihexagonal		3.4.6.4
Teselado trihexagonal truncado		4.6.12
Teselado trihexagonal romo		3.3.3.3.6
Teselado triangular elongado		3.3.3.4.4

La familia de los teselados de caras regulares que no son uniformes en infinita.

Los deltaedros son poliedros cuyas caras son todas triángulos equiláteros:

• Los 8 deltaedros convexos:

Nombre	Imagen
Tetraedro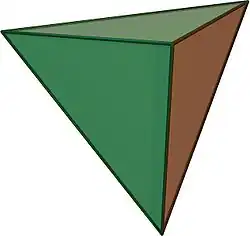
Octaedro
Icosaedro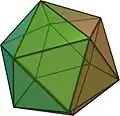
Bipirámide triangular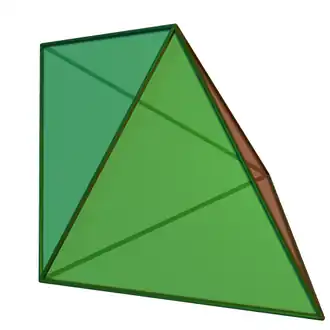
Bipirámide pentagonal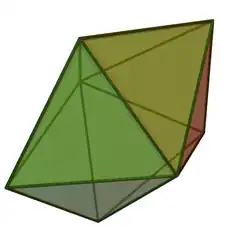
Biesfenoide romo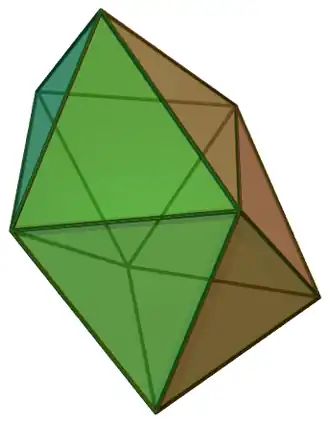
Prisma triangular triaumentado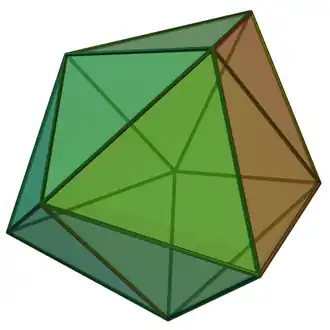
Bipirámide cuadrada giroelongada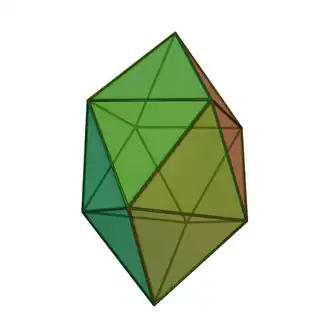

• La familia infinita de los deltaedros no convexos

Los policubos son poliedros de caras cuadradas cuyos ángulos diedros siempre corresponden a múltiplos de 90°. Su construcción se puede describir como una unión de cualquier cantidad de cubos por sus caras.

• Teselados de polígonos regulares
• Poliedro
• Poliedro uniforme
• Polígono regular

1. ↑ «Regular-faced Polyhedra». tupelo-schneck.org. Consultado el 26 de julio de 2025. 
2. ↑ Coxeter Groups. Cambridge University Press. 12 de diciembre de 2002. pp. 64-94. Consultado el 26 de julio de 2025.