Método del volumen de fluidos

En la dinámica de fluidos computacional, el método del volumen de fluido (VOF) es una familia de técnicas de modelización de superficies libres, es decir, técnicas numéricas para rastrear y localizar la superficie libre (o interfaz fluido-fluido). Pertenecen a la clase de métodos eulerianos, que se caracterizan por una malla que es estacionaria o se mueve de una manera determinada para adaptarse a la forma cambiante de la interfaz. Como tales, los métodos VOF son esquemas de advección que capturan la forma y la posición de la interfaz, pero no son algoritmos independientes para resolver flujos. Las ecuaciones de Navier-Stokes que describen el movimiento del flujo deben resolverse por separado.

El método del volumen de fluido se basa en los métodos anteriores Marcadores y células (MAC)^[1]​^[2]​ desarrollado en Los Alamos National Laboratory. MAC utilizó partículas marcadoras lagrangianas para rastrear la distribución del fluido en una cuadrícula euleriana fija. El uso de partículas marcadoras era computacionalmente costoso porque requería muchas partículas marcadoras por celda de la cuadrícula, para reducir el ruido numérico cuando las partículas marcadoras discretas se movían a través de las celdas de la cuadrícula. La idea original del método VOF era sustituir las partículas marcadoras por una única variable escalar por celda de la cuadrícula que representara la fracción de volumen del fluido en ella. De este modo, el volumen del fluido se rige por una ecuación de advección. Esta idea surgió de estudios sobre problemas de mezclas bifásicas (agua y vapor), en los que era habitual utilizar una variable de volumen de vapor.^[3]​ El enfoque VOF se demostró por primera vez en una publicación de 1975 titulada «Methods for Calculating Multi-Dimensional, Transient Free Surface Flows Past Bodies» (Métodos para calcular flujos multidimensionales y transitorios de superficie libre que pasan por cuerpos), de Nichols y Hirt.^[4]​ Esta publicación describía cómo transportar la fracción de fluido con un esquema donante-aceptor, cómo estimar la orientación y la posición de la superficie libre dentro de las celdas superficiales y cómo prescribir las condiciones de contorno adecuadas (continuidad y esfuerzo cortante nulo) en la superficie libre. Este enfoque era mucho más sencillo que otras técnicas de seguimiento de la superficie del fluido, pero más versátil, ya que podía modelar la coalescencia y la ruptura de regiones fluidas. En 1976, Noh y Woodward^[5]​ presentó el Simple Line Interface Calculation (SLIC), una técnica para aproximar interfaces fluidas basada en fracciones de volumen, diseñada para el esquema de advección de fracciones de volumen con división direccional. El SLIC también podía manejar un número arbitrario de fases fluidas inmiscibles por celda de la cuadrícula. Por lo tanto, el SLIC se adaptaba bien al enfoque VOF, aunque ambos métodos eran inicialmente independientes y permanecieron separados hasta los años 90. El término «método del volumen de fluido» y su acrónimo «método VOF» se acuñaron en el informe del Laboratorio Científico de Los Álamos de 1980, «SOLA-VOF: A Solution Algorithm for Transient Fluid Flow with Multiple Free Boundaries», de Nichols, Hirt y Hotchkiss^[6]​ y en la publicación de la revista «Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries» de Hirt y Nichols en 1981.^[7]​ Estas dos publicaciones proporcionaron más detalles sobre los procedimientos específicos utilizados para aproximar la posición de la superficie libre (representada localmente por una línea inclinada en las celdas de la superficie) y aplicar las condiciones de contorno de la superficie libre sobre ella. Dado que el método VOF superó al MAC al reducir los requisitos de almacenamiento informático, rápidamente se hizo popular. Las primeras aplicaciones del programa SOLA-VOF desarrollado en Los Álamos incluyen estudios de seguridad de reactores de agua ligera.^[8]​^[9]​ La NASA también adoptó una variante del código SOLA-VOF.^[10]​^[11]​ En 1982, Youngs desarrolló el esquema de cálculo de interfaz lineal por tramos (PLIC),^[12]​ que mejoró la precisión de la reconstrucción de la interfaz con respecto al SLIC y los primeros métodos VOF.^[13]​

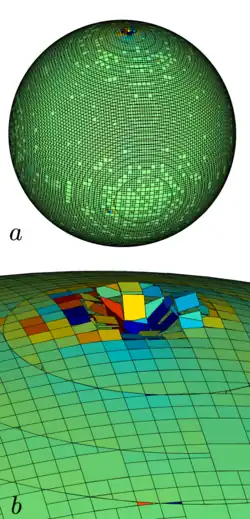
El método se basa en la idea de una función denominada «función de fracción» ${\displaystyle C}$. Se trata de una función escalar, definida como la integral de la función característica de un fluido en el volumen de control, es decir, el volumen de una celda de la red computacional. La fracción de volumen de cada fluido se rastrea a través de cada celda de la malla computacional, mientras que todos los fluidos comparten un único conjunto de ecuaciones de momento, es decir, una por cada dirección espacial. Desde una perspectiva promediada por el volumen de la celda, cuando una celda está vacía de la fase rastreada, el valor de ${\displaystyle C}$ es cero; cuando la celda está llena de la fase rastreada, ${\displaystyle C=1}$; y cuando la celda contiene una interfaz entre los volúmenes rastreados y no rastreados, ${\displaystyle 0<C<1}$. Desde la perspectiva de un punto local que no contiene volumen, ${\displaystyle C}$ es una función discontinua en la medida en que su valor salta de 0 a 1 cuando el punto local se mueve de la fase no rastreada a la fase rastreada. La dirección normal de la interfaz del fluido se encuentra donde el valor de ${\displaystyle C}$ cambia más rápidamente. Con este método, la superficie libre no se define con precisión, sino que se distribuye a lo largo de la altura de una celda. Por lo tanto, para obtener resultados precisos, es necesario realizar refinamientos locales de la malla. El criterio de refinamiento es sencillo: las celdas con ${\displaystyle 0<C<1}$ deben refinarse. Raad y sus colegas desarrollaron un método para ello, conocido como método de marcadores y microcélulas, en 1997.^[14]​

La evolución del fluido ${\displaystyle m}$ en un sistema de ${\displaystyle n}$ fluidos se rige por la ecuación de transporte (en realidad, la misma ecuación que debe cumplir la función de distancia ${\displaystyle \phi }$ del Método del conjunto de nivel):

${\displaystyle {\frac {\partial C_{m}}{\partial t}}+\mathbf {v} \cdot \nabla C_{m}=0,}$

con la siguiente restricción

${\displaystyle \sum _{m=1}^{n}C_{m}=1}$,

Es decir, el volumen de los fluidos es constante. Para cada celda, se calculan propiedades como la densidad ${\displaystyle \rho }$ mediante una media de la fracción de volumen de todos los fluidos de la celda.

${\displaystyle \rho =\sum _{m=1}^{n}\rho _{m}C_{m}.}$

Estas propiedades se utilizan a continuación para resolver una única ecuación de momento a través del dominio, y el campo de velocidad obtenido se comparte entre los fluidos.

El método VOF es fácil de calcular, ya que solo introduce una ecuación adicional y, por lo tanto, requiere un almacenamiento mínimo. El método también se caracteriza por su capacidad para tratar problemas altamente no lineales en los que la superficie libre experimenta cambios topológicos bruscos. Al utilizar el método VOF, también se evita el uso de complicados algoritmos de deformación de mallas utilizados por los métodos de seguimiento de superficies. La principal dificultad asociada al método es la difuminación de la superficie libre. Este problema se origina por la difusión excesiva de la ecuación de transporte.

Para evitar la difuminación de la superficie libre, la ecuación de transporte debe resolverse sin una difusión excesiva. Por lo tanto, el éxito de un método VOF depende en gran medida del esquema utilizado para la advección del campo ${\displaystyle C}$. Cualquier esquema elegido debe tener en cuenta el hecho de que ${\displaystyle C}$ es discontinuo, a diferencia, por ejemplo, de la función de distancia ${\displaystyle \phi }$ utilizada en el Método del conjunto de nivel.

Mientras que un esquema de primer orden a favor del viento difumina la interfaz, un esquema del mismo orden en contra del viento provocará un problema de distribución falsa que causará un comportamiento errático en caso de que el flujo no esté orientado a lo largo de una línea de la cuadrícula. Dado que estos esquemas de orden inferior son inexactos y los de orden superior son inestables e inducen oscilaciones, ha sido necesario desarrollar esquemas que mantengan la superficie libre nítida y, al mismo tiempo, produzcan perfiles monótonos para ${\displaystyle C}$.^[15]​ A lo largo de los años, se han desarrollado multitud de métodos diferentes para tratar la advección. En el artículo original sobre VOF de Hirt, se empleó un . Este esquema sentó las bases para los esquemas de diferenciación compresiva.

Los diferentes métodos para tratar el VOF se pueden dividir a grandes rasgos en tres categorías: la formulación «donante-aceptor», los esquemas de «diferenciación de orden superior» y las «técnicas de línea».

El esquema donante-aceptor se basa en dos criterios fundamentales, a saber, el criterio de limitación y el criterio de disponibilidad. El primero establece que el valor de ${\displaystyle C}$ debe estar limitado entre cero y uno. El segundo criterio garantiza que la cantidad de fluido convectado sobre una cara durante un intervalo de tiempo sea menor o igual que la cantidad disponible en la celda donante, es decir, la celda desde la que fluye el fluido hacia la celda aceptora. En su trabajo original, Hirt trató este tema con un esquema mixto que consistía en una diferencia controlada hacia abajo y hacia arriba.

En los esquemas de diferenciación de orden superior, como su nombre indica, la ecuación de transporte convectivo se discretiza con esquemas de diferenciación de orden superior o combinados. Entre estos métodos se encuentra el Esquema de Captura de Interfaces Compresivas para Mallas Arbitrarias (CICSAM) ^[16]​ y Captura de Interfaces de Alta Resolución (HRIC) ^[17]​ esquema, ambos basados en el diagrama variable normalizado (NVD) de Leonard.^[18]​

Las técnicas de línea evitan los problemas asociados con la discretización de la ecuación de transporte al no rastrear explícitamente la interfaz en una celda. En su lugar, la distribución del fluido en una celda se obtiene utilizando la distribución de la fracción de volumen de las celdas vecinas. El cálculo de interfaz de línea simple (SLIC) de Noh y Woodward de 1976^[5]​ utiliza una geometría simple para reconstruir la interfaz. En cada celda, la interfaz se aproxima como una línea paralela a uno de los ejes de coordenadas y asume diferentes configuraciones de fluidos para los movimientos horizontales y verticales, respectivamente. Una técnica muy utilizada hoy en día es el cálculo de interfaz lineal por tramos de Youngs. ^[20]​ PLIC se basa en la idea de que la interfaz puede representarse como una línea en R² o un plano en R³; en este último caso, podemos describir la interfaz mediante:

${\displaystyle \mathbf {n} _{x}+\mathbf {n} _{y}+\mathbf {n} _{z}=\alpha ,}$

donde ${\displaystyle \mathbf {n} }$ es un vector normal a la interfaz. Los componentes de la normal se encuentran, por ejemplo, utilizando el método de diferencias finitas o su combinación con la optimización de mínimos cuadrados. A continuación, se encuentra el término libre ${\displaystyle \alpha }$ (analíticamente o por aproximación) imponiendo la conservación de la masa dentro de la celda computacional. Una vez establecida la descripción de la interfaz, se resuelve la ecuación de advección de ${\displaystyle C}$ utilizando técnicas geométricas como la búsqueda del flujo de ${\displaystyle C}$ entre las celdas de la malla, o la advección de los extremos de la interfaz utilizando valores discretos de la velocidad del fluido.

En flujos bifásicos en los que las propiedades de las dos fases son muy diferentes, los errores en el cálculo de la fuerza de tensión superficial en la interfaz provocan que los métodos de captura frontal, como el volumen de fluido (VOF) y el método de nivel establecido (LS), desarrollen corrientes espurias interfaciales. Para resolver mejor estos flujos, se requiere un tratamiento especial para reducir dichas corrientes espurias. Algunos estudios han analizado la mejora del seguimiento de la interfaz combinando el método de nivel establecido y los métodos de volumen de fluido, mientras que otros han analizado la mejora del algoritmo de resolución numérica añadiendo bucles de suavizado o mejorando las técnicas de promediado de propiedades.^[21]​

• Método de los contornos inmersos
• Método de Euler-Lagrange estocástico
• Método del conjunto de nivel
• Dinámica del chapoteo