Derivadas objetivas de la tensión

En mecánica del continuo, las derivadas objetivas de tensión o tasas de cambio objetivas para la tensión son derivadas temporales de la tensión mecánica que no dependen del sistema de referencia.^[1]​

Muchas ecuaciones constitutivas se diseñan en forma de una relación entre el incremento de tensión y una velocidad de deformación (o el tensor de tasa de deformación). Además en estas condiciones, la respuesta mecánica de un material no debería depender del sistema de referencia por el principio de objetividad material. En otras palabras, las ecuaciones constitutivas del material deberían ser independientes del marco de referencia (objetivas). Si las tensiones y las medidas de deformación son cantidades materiales (lagrangianas), entonces la objetividad se satisface automáticamente. Sin embargo, si las cantidades son espaciales (eulerianas), la objetividad de la tasa de tensión no se satisface automáticamente, aun cuando la tasa de deformación sea objetiva.

Existen numerosas tasas de tensión objetivas en mecánica de medios continuos, todas ellas son formas especiales de la derivada de Lie. Algunas de las tasas de tensión objetivas más utilizadas son:

• La tasa de Truesdell de la tensión de Cauchy,
• La tasa de Green–Naghdi de la tensión de Cauchy, y la tasa de Zaremba-Jaumann de la tensión de Cauchy. ^[2]​

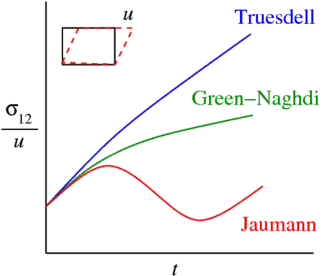
La figura 1 se muestra el comportamiento de varias tasas de tensión objetivas en un esayo de cizalladura simple, donde el modelo de material es hipoelástico con módulos elásticos constantes. Se grafica el cociente entre la tensión cortante y el desplazamiento como una función del tiempo. Se utilizan los mismos módulos con las tres tasas de cambio objetivas para la tensión. Claramente, se observan oscilaciones espurias para la tasa de tensión de Zaremba-Jaumann.^[3]​ Esto no se debe a que una tasa sea mejor que otra, sino al uso incorrecto de los modelos de material aplicar las mismas constantes con diferentes tasas objetivas.^[4]​ Por esta razón, una tendencia reciente ha sido evitar las tasas de tensión objetivas siempre que sea posible.^{[cita requerida]}

Es relatividamente sencillo comprobar que la derivada temporal de la tensión de Cauchy no es materialmente objetiva: bajo rotaciones de cuerpo rígido (${\displaystyle {\boldsymbol {Q}}}$), el tensor de tensión de Cauchy ${\displaystyle {\boldsymbol {\sigma }}}$ se transforma como

$${\displaystyle {\boldsymbol {\sigma }}_{r}={\boldsymbol {Q}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {Q}}^{T}~;~~{\boldsymbol {Q}}\cdot {\boldsymbol {Q}}^{T}={\boldsymbol {\mathit {1}}}}$$

Dado que ${\displaystyle {\boldsymbol {\sigma }}}$ es una cantidad espacial y la transformación sigue las reglas de las transformaciones tensoriales, ${\displaystyle {\boldsymbol {\sigma }}}$ es objetiva. Sin embargo,

$${\displaystyle {\cfrac {d}{dt}}({\boldsymbol {\sigma }}_{r})={\dot {\boldsymbol {\sigma }}}_{r}={\dot {\boldsymbol {Q}}}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {Q}}^{T}+{\boldsymbol {Q}}\cdot {\dot {\boldsymbol {\sigma }}}\cdot {\boldsymbol {Q}}^{T}+{\boldsymbol {Q}}\cdot {\boldsymbol {\sigma }}\cdot {\dot {\boldsymbol {Q}}}^{T}\neq {\boldsymbol {Q}}\cdot {\dot {\boldsymbol {\sigma }}}\cdot {\boldsymbol {Q}}^{T},.}$$

Por lo tanto, la tasa de tensión no es objetiva a menos que la tasa de rotación sea cero, es decir, ${\displaystyle {\boldsymbol {Q}}}$ sea constante.

Para una comprensión física de lo anterior, consideremos la situación mostrada en la Figura 2. En la figura, los componentes del tensor de tensión de Cauchy (o tensión verdadera) se denotan con los símbolos ${\displaystyle S_{ij}}$. Este tensor, que describe las fuerzas en un pequeño elemento material imaginado como extraído del material en su estado deformado actual, no es objetivo en grandes deformaciones porque varía con las rotaciones de cuerpo rígido del material. Los puntos materiales deben caracterizarse por sus coordenadas lagrangianas iniciales ${\displaystyle X_{i}}$. En consecuencia, es necesario introducir la llamada tasa de tensión objetiva ${\displaystyle {\overset {\circ }{S}}{ij}}$, o el incremento correspondiente ${\displaystyle \Delta S{ij}={\overset {\circ }{S}}{ij}\Delta t}$. La objetividad es necesaria para que ${\displaystyle {\overset {\circ }{S}}{ij}}$ esté funcionalmente relacionada con la deformación del elemento. Esto significa que ${\displaystyle {\overset {\circ }{S}}_{ij}}$ debe ser invariante bajo transformaciones de coordenadas, particularmente bajo rotaciones de cuerpo rígido, y debe caracterizar el estado del mismo elemento material mientras se deforma.

La tasa de tensión objetiva se puede derivar de dos maneras:

• Mediante transformaciones tensoriales de coordenadas,^[5]​ que es el método estándar en libros de texto de elementos finitos^[6]​
• De manera variacional, a partir de la densidad de energía de deformación del material expresada en términos del tensor de deformación (que es objetivo por definición)^[7]​^[8]​

Si bien el primer método es instructivo y proporciona una visión geométrica útil, el segundo método es matemáticamente más corto y tiene la ventaja adicional de garantizar automáticamente la conservación de la energía, es decir, asegurar que el trabajo de segundo orden del tensor de incremento de tensión sobre el tensor de incremento de deformación sea correcto (requisito de conjugación del trabajo).

La relación matemática entre la tensión de Cauchy y el segundo tensor de Piola-Kirchhoff es la llamada transformación de Piola que resulta ser la aplicación regrediente (pull-back) asociada al cambio de coordenadas del tensor de tensiones de Cauchy ${\displaystyle {\boldsymbol {\sigma }}}$ o equivalentemente la aplicación progrediente (push-forward) de ${\displaystyle {\boldsymbol {S}}}$, es decir:

$${\displaystyle {\boldsymbol {S}}=J~\phi ^{*}[{\boldsymbol {\sigma }}]~;~~{\boldsymbol {\sigma }}=J^{-1}~\phi _{*}[{\boldsymbol {S}}]}$$

En esas condiciones, la tasa de cambio de Truesdell para la tensión de Cauchy se define como la transformación de Piola de la derivada material respecto al tiempo del segundo tensor de Piola-Kirchhoff:

$${\displaystyle {\overset {\circ }{\boldsymbol {\sigma }}}=J^{-1}~\phi _{*}[{\dot {\boldsymbol {S}}}]}$$

Expandiendo esta expresión se tiene que:

$${\displaystyle {\overset {\circ }{\boldsymbol {\sigma }}}=J^{-1}~{\boldsymbol {F}}\cdot {\dot {\boldsymbol {S}}}\cdot {\boldsymbol {F}}^{T}=J^{-1}~{\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left(J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}\right)\right]\cdot {\boldsymbol {F}}^{T}=J^{-1}~{\mathcal {L}}_{\varphi }[{\boldsymbol {\tau }}]}$$

donde la tensión de Kirchhoff ${\displaystyle {\boldsymbol {\tau }}=J~{\boldsymbol {\sigma }}}$ y la derivaada de Lie de la tensión de Kirchhoff vienen dadas por:

$${\displaystyle {\mathcal {L}}_{\varphi }[{\boldsymbol {\tau }}]={\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}\right)\right]\cdot {\boldsymbol {F}}^{T}~.}$$

Esta última expresión se puede simplificar a la expresión de la tasa de cambio Truesdell para la tensión de Cauchy:

Este es una forma especial para la dereivada de Lie (o tasa de Truesdell). Nótese que la tasa de Truesdell para la tensión de Cauchy viene dada por

$${\displaystyle {\overset {\circ }{\boldsymbol {\sigma }}}=J^{-1}~{\boldsymbol {F}}\cdot \left[{\cfrac {d}{dt}}\left(J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}\right)\right]\cdot {\boldsymbol {F}}^{T}~.}$$

Y, por tanto, del teorema de descomposición polar tenemos que:

$${\displaystyle {\boldsymbol {F}}={\boldsymbol {R}}\cdot {\boldsymbol {U}}}$$

donde ${\displaystyle {\boldsymbol {R}}}$ es una matriz de rotación (${\displaystyle {\boldsymbol {R}}^{-1}={\boldsymbol {R}}^{T}}$) y ${\displaystyle {\boldsymbol {U}}}$ es el tensor derecho de estiramiento que es simétrico y definido positivo.

Si asumimos que ${\displaystyle {\boldsymbol {U}}={\boldsymbol {\mathit {1}}}}$ we get ${\displaystyle {\boldsymbol {F}}={\boldsymbol {R}}}$. Cuando no hay estiramiento ${\displaystyle J=1}$ y tenemos ${\displaystyle {\boldsymbol {\tau }}={\boldsymbol {\sigma }}}$. Nótse que esto no significa que no haya estiramiento físico en el cuerpo físico -es sólo una simplificación con el propósito de definir una tasa de cambio objetiva para tensión. Por tanto,

$${\displaystyle {\overset {\circ }{\boldsymbol {\sigma }}}={\boldsymbol {R}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {R}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {R}}^{-T}\right)\right]\cdot {\boldsymbol {R}}^{T}={\boldsymbol {R}}\cdot \left[{\cfrac {d}{dt}}\left({\boldsymbol {R}}^{T}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {R}}\right)\right]\cdot {\boldsymbol {R}}^{T}}$$

Puede demostrarse que esta expresión se puede simplificar a la forma conocida como tasa de Green-Naghdi:

• J.E. Marsden, T.J. Hughes, Mathematical Foundations of Elasticity, Dover, ISBN 0-486-67865-2
• R.W. Ogden, Non-linear Elastic Deformation, Dover, ISBN 0-486-69648-0
• G.A. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Wiley, 2000
• A.I. Lurie, Theory of Elasticity, Springer, 1999.
• L.B. Freund, Dynamic Fracture Mechanics, Cambridge University Press, 1990.
• J. Ignaczak, M. Ostoja-Starzewski, Thermoelasticity with Finite Wave Speeds, Oxford University Press, 2010.
• D. Bigoni, Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability, Cambridge University Press, 2012.
• Y. C. Fung, Pin Tong and Xiaohong Chen, Classical and Computational Solid Mechanics, 2nd Edition, World Scientific Publishing, 2017, ISBN 978-981-4713-64-1.