Teorema de Erdös-Ko-Rado

En matemáticas, el teorema de Erdős-Ko-Rado limita el número de subconjuntos que forman parte de una familia de subconjuntos de un conjunto dado, cuando cada dos de estos subconjuntos tienen al menos un elemento en común. Paul Erdős, Chao Ko y Richard Rado demostraron el teorema en 1938, pero no lo publicaron hasta 1961. Forma parte del campo de la combinatoria y es uno de los resultados centrales de la teoría de conjuntos extremos.^[1]​

El teorema se aplica a familias de subconjuntos que tienen todos el mismo tamaño ${\displaystyle r}$, y son todos subconjuntos de algún conjunto mayor de tamaño ${\displaystyle n}$. Una forma de construir una familia de conjuntos con estos parámetros, de forma que cada dos de ellos compartan un elemento, es elegir un único elemento que pertenezca a todos los subconjuntos y, a continuación, formar todos los subconjuntos que contengan el elemento elegido. El teorema de Erdős-Ko-Rado establece que cuando ${\displaystyle n}$ es lo suficientemente grande para que el problema no sea trivial (es decir, para ${\displaystyle n\geq 2r}$) esta construcción produce las mayores familias de intersección posibles. Cuando ${\displaystyle n=2r}$ hay otras familias igual de grandes, pero para valores mayores de ${\displaystyle n}$ sólo las familias así construidas pueden ser más grandes.

El teorema de Erdős-Ko-Rado también puede describirse en términos de hipergrafos o conjuntos independientes en grafos de Kneser. Varios teoremas análogos se aplican a otros tipos de objetos matemáticos distintos de los conjuntos, incluidos los subespacios lineales, las permutaciones y las cadenas. También describen las familias de intersección más grandes posibles como las que se forman eligiendo un elemento y formando la familia de todos los objetos que contienen el elemento elegido.

Supóngase que ${\displaystyle {\mathcal {A}}}$ es una familia de subconjuntos con ${\displaystyle r}$-elementos distintos, que pertenecen a un conjunto de ${\displaystyle n}$-elementos con ${\displaystyle n\geq 2r}$, y que cada dos subconjuntos comparten al menos un elemento. Entonces, el teorema establece que el número de subconjuntos en ${\displaystyle {\mathcal {A}}}$ es como máximo el coeficiente binomial

$${\displaystyle {\binom {n-1}{r-1}}}$$

El requisito de que ${\displaystyle n\geq 2r}$ sea necesario para que el problema no sea trivial, se debe a que cuando ${\displaystyle n<2r}$, todos los subconjuntos de ${\displaystyle r}$-elementos se intersecan, y la familia de intersecciones más grande consiste en todos los conjuntos de ${\displaystyle r}$-elementos, con tamaño ${\displaystyle {\tbinom {n}{r}}}$.^[2]​

El mismo resultado puede formularse como parte de la teoría de hipergrafos. Una familia de conjuntos también puede denominarse hipergrafo, y cuando todos los conjuntos (que en este contexto se denominan "hiperaristas") tienen el mismo tamaño ${\displaystyle r}$, se denomina hipergrafo ${\displaystyle r}$-uniforme. Por lo tanto, el teorema proporciona un límite superior para el número de hiperaristas superpuestas por pares en un hipergrafo ${\displaystyle r}$-uniforme con ${\displaystyle n}$ vértices y ${\displaystyle n\geq 2r}$.^[3]​

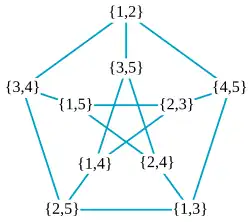
El teorema también puede formularse en términos de teoría de grafos: el conjunto independiente del grafo de Kneser ${\displaystyle KG_{n,r}}$ para ${\displaystyle n\geq 2r}$ es

$${\displaystyle \alpha (KG_{n,r})={\binom {n-1}{r-1}}.}$$

Este es un grafo con un vértice para cada subconjunto de ${\displaystyle r}$-elementos de un conjunto de ${\displaystyle n}$-elementos y una arista entre cada par de conjuntos disjuntos. Un conjunto independiente es una colección de vértices que no tiene aristas entre sus pares, y el número de independencia es el tamaño del conjunto independeinte.^[4]​ más grande. Dado que los grafos de Kneser tienen simetrías que llevan cualquier vértice a cualquier otro vértice (son grafos de vértices transitivos), su número cromático fraccionario es igual al cociente de su número de vértices y de su número de independencia. Por lo tanto, otra forma de expresar el teorema de Erdos-Ko-Rado es que estos grafos tienen un número cromático fraccionario que vale exactamente ${\displaystyle n/r}$.^[5]​

Paul Erdős, Chao Ko y Richard Rado demostraron este teorema en 1938 tras trabajar juntos en Inglaterra. Rado se había mudado de Berlín a la Universidad de Cambridge y Erdos de Hungría a la Universidad de Mánchester, ambos escapando de la influencia de la Alemania nazi. Ko fue alumno de Louis Mordell en Mánchester.^[6]​ Sin embargo, no publicaron el resultado hasta 1961,^[7]​ debido, en parte, a la falta de interés en la teoría de conjuntos combinatorios en la década de 1930 y al creciente interés en el tema en la década de 1960.^[6]​ El artículo de 1961 planteó el resultado de una forma aparentemente más general, en la que solo se requería que los subconjuntos tuvieran un tamaño al menos de ${\displaystyle r}$, y satisficieran el requisito adicional de que ningún subconjunto estuviera contenido en ningún otro.^[7]​ Una familia de subconjuntos que cumpla estas condiciones puede ampliarse a subconjuntos de tamaño exactamente ${\displaystyle r}$ mediante la aplicación del teorema de Hall,^[8]​ o seleccionando cada subconjunto ampliado de la misma cadena en una descomposición en una cadena de conjuntos simétrica.^[9]​

Una forma sencilla de construir una familia de subconjuntos de ${\displaystyle r}$-elementos que se intersecan, cuyo tamaño coincida exactamente con la cota de Erdos-Ko-Rado, es elegir cualquier elemento fijo ${\displaystyle x}$ y que ${\displaystyle {\mathcal {A}}}$ conste de todos los subconjuntos de ${\displaystyle r}$-elementos que incluyan a ${\displaystyle x}$. Por ejemplo, para los subconjuntos de 2 elementos del conjunto ${\displaystyle \{1,2,3,4\}}$, de 4 elementos, con ${\displaystyle x=1}$, esto produce la familia

${\displaystyle \{1,2\}}$, ${\displaystyle \{1,3\}}$, y ${\displaystyle \{1,4\}}$.

Dos subconjuntos cualesquiera de esta familia se intersecan, porque ambos incluyen a ${\displaystyle 1}$. El número de conjuntos es ${\displaystyle {\tbinom {n-1}{r-1}}}$, ya que, tras elegir el elemento fijo, quedan ${\displaystyle n-1}$ elementos adicionales por elegir, y cada conjunto elige ${\displaystyle r-1}$ de estos elementos restantes.^[10]​

Cuando ${\displaystyle n>2r}$ esta es la única familia de este tamaño que se interseca. Sin embargo, cuando ${\displaystyle n=2r}$, existe una construcción más general. Cada subconjunto de ${\displaystyle r}$-elementos puede emparejarse con su complemento, el único subconjunto de ${\displaystyle r}$-elementos del que es disjunto. A continuación, se elige un subconjunto de cada uno de estos pares complementarios. Por ejemplo, para los mismos parámetros anteriores, esta construcción más general puede utilizarse para formar la familia

${\displaystyle \{3,4\}}$, ${\displaystyle \{2,4\}}$, y ${\displaystyle \{2,3\}}$,

donde dos subconjuntos se intersecan a pesar de que ningún elemento pertenece a los tres conjuntos. En este ejemplo, todos los conjuntos se han complementado a partir de los del primer ejemplo, pero también es posible complementar solo algunos subconjuntos.^[10]​

Cuando ${\displaystyle n>2r}$, las familias del primer tipo (conocidas también como estrellas,^[11]​ dictaduras,^[12]​ juntas,^[12]​ familias centradas,^[13]​ o familias principales,^[14]​ son las únicas familias máximas. En este caso, una familia de tamaño casi máximo tiene un elemento común a casi todos sus subconjuntos.^[15]​ Esta propiedad se ha denominado estabilidad,^[14]​ aunque el mismo término también se ha utilizado para una propiedad diferente: el hecho de que (para un amplio rango de parámetros) eliminar aristas elegidas aleatoriamente del grafo de Kneser no aumenta el tamaño de sus subconjuntos independientes.^[16]​

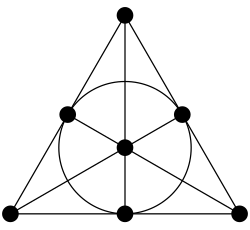
Una familia intersecante de subconjuntos de ${\displaystyle r}$-elementos puede ser máximal, ya que no se puede añadir ningún otro subconjunto (ni siquiera extendiendo el conjunto base) sin destruir la propiedad de intersección, pero no de tamaño máximo. Un ejemplo con ${\displaystyle n=7}$ y ${\displaystyle r=3}$ es el conjunto de siete rectas del plano de Fano, mucho menor que el límite de Erdos-Ko-Rado de 15.^[17]​ De manera más general, las rectas de cualquier plano proyectivo de orden ${\displaystyle q}$ forman una familia de intersección máxima que incluye solo ${\displaystyle n}$ subconjuntos, para los parámetros ${\displaystyle r=q+1}$ and ${\displaystyle n=q^{2}+q+1}$. El plano de Fano es el caso con ${\displaystyle q=2}$ de esta construcción.^[18]​

El tamaño más pequeño posible de una familia de intersección máximal de subconjuntos de ${\displaystyle r}$-elementos, en términos de ${\displaystyle r}$, es desconocido, pero al menos es ${\displaystyle 3r}$ para ${\displaystyle r\geq 4}$.^[19]​ Los planos proyectivos producen familias de intersección maximales cuyo número de subconjuntos es ${\displaystyle r^{2}-r+1}$, pero para infinitas elecciones de ${\displaystyle r}$ existen familias de intersección maximales más pequeñas de tamaño ${\displaystyle {\tfrac {3}{4}}r^{2}}$.^[18]​

Las familias de subconjuntos intersecantes de ${\displaystyle r}$-elementos que son maximales pero no máximas, tienen un tamaño de $${\displaystyle {\binom {n-1}{r-1}}-{\binom {n-r-1}{r-1}}+1.}$$ Se forman a partir de un elemento ${\displaystyle x}$ y de un conjunto ${\displaystyle Y}$ de ${\displaystyle r}$-elementos que no contiene a ${\displaystyle x}$, añadiendo ${\displaystyle Y}$ a la familia de subconjuntos de ${\displaystyle r}$-elementos que incluye tanto a ${\displaystyle x}$ como al menos un elemento de ${\displaystyle Y}$. Este resultado se denomina «teorema de Hilton-Milner», tras su demostración por parte de Anthony Hilton y de Eric Charles Milner en 1967.^[20]​

La demostración original del teorema de Erdos-Ko-Rado utilizaba el procedimiento de inducción sobre ${\displaystyle n}$. El caso base, para ${\displaystyle n=2r}$, se deduce fácilmente del hecho de que una familia intersecante no puede incluir tanto un subconjunto como su complemento, y que en este caso la cota del teorema de Erdos-Ko-Rado es exactamente la mitad del número de todos los subconjuntos de ${\displaystyle r}$-elementos. El paso de inducción para valores de ${\displaystyle n}$ mayores utiliza un método llamado cambio, que consiste en sustituir elementos en familias intersecantes para reducir la familia en orden lexicográfico y reducirla a una forma canónica más fácil de analizar.^[21]​

En 1972, Gyula O. H. Katona presentó la siguiente demostración breve, utilizando el doble conteo:^[22]​

Sea ${\displaystyle {\mathcal {A}}}$ cualquier familia intersecante de subconjuntos de ${\displaystyle r}$-elementos de un conjunto de ${\displaystyle n}$-elementos. Ordénense todos los ${\displaystyle n}$ elementos en cualquier orden cíclico y considérense los subconjuntos de ${\displaystyle {\mathcal {A}}}$ que forman intervalos de longitud ${\displaystyle r}$ dentro de este orden cíclico elegido. Por ejemplo, si ${\displaystyle n=8}$ y ${\displaystyle r=3}$, un posible orden cíclico para los números ${\displaystyle \{1,2,...,8\}}$ es ${\displaystyle (3,1,5,4,2,7,6,8)}$, que tiene ocho intervalos de 3 elementos (incluidos los que se envuelven):

${\displaystyle (3,1,5)}$, ${\displaystyle (1,5,4)}$, ${\displaystyle (5,4,2)}$, ${\displaystyle (4,2,7)}$, ${\displaystyle (2,7,6)}$, ${\displaystyle (7,6,8)}$, ${\displaystyle (6,8,3)}$, and ${\displaystyle (8,3,1)}$.

Sin embargo, solo algunos de estos intervalos pueden pertenecer a ${\displaystyle {\mathcal {A}}}$, ya que no todos se intersecan. La observación clave de Katona es que como máximo ${\displaystyle r}$ intervalos de un solo orden cíclico pueden pertenecer a to ${\displaystyle {\mathcal {A}}}$. Esto se debe a que, si ${\displaystyle (a_{1},a_{2},\dots ,a_{r})}$ es uno de estos intervalos, entonces cualquier otro intervalo del mismo orden cíclico que pertenece a ${\displaystyle {\mathcal {A}}}$ separa ${\displaystyle a_{i}}$ from ${\displaystyle a_{i+1}}$, de algún ${\displaystyle i}$, al contener precisamente uno de estos dos elementos. Los dos intervalos que separan estos elementos son disjuntos, por lo que como máximo uno de ellos puede pertenecer a ${\displaystyle {\mathcal {A}}}$. Por lo tanto, el número de intervalos en ${\displaystyle {\mathcal {A}}}$ es como máximo uno más el número de ${\displaystyle r-1}$ pares que pueden ser separados.^[22]​

Basándose en esta idea, es posible contar pares ${\displaystyle (S,C)}$, donde ${\displaystyle S}$ es un subconjunto en ${\displaystyle {\mathcal {A}}}$ y ${\displaystyle C}$ es un orden cíclico para el cual ${\displaystyle S}$ es un intervalo, de dos maneras. Primero, para cada subconjunto ${\displaystyle S}$ se puede generar ${\displaystyle C}$ eligiendo una de las ${\displaystyle r!}$ permutaciones de ${\displaystyle S}$ y las ${\displaystyle (n-r)!}$ permutaciones de los elementos restantes, mostrando que el número de pares es ${\displaystyle |{\mathcal {A}}|r!(n-r)!}$. Segundo, existen ${\displaystyle (n-1)!}$ órdenes cíclicos, cada uno de los cuales tiene como máximo ${\displaystyle r}$ intervalos de ${\displaystyle {\mathcal {A}}}$, por lo que el número de pares es más de ${\displaystyle r(n-1)!}$. Comparando estos dos conteos se obtiene la desigualdad $${\displaystyle |{\mathcal {A}}|r!(n-r)!\leq r(n-1)!}$$ y dividiendo ambos lados por ${\displaystyle r!(n-r)!}$ se obtiene el resultado^[22]​

$${\displaystyle |{\mathcal {A}}|\leq {\frac {r(n-1)!}{r!(n-r)!}}={n-1 \choose r-1}.}$$

También es posible deducir el teorema de Erdos-Ko-Rado como un caso especial del teorema de Kruskal–Katona, otro resultado importante en teoría de conjuntos extremales.^[23]​ Muchas otras demostraciones son conocidas.^[24]​

Una generalización del teorema se aplica a subconjuntos que requieren intersecciones grandes. Esta versión del teorema tiene tres parámetros: ${\displaystyle n}$ (el número de elementos de los que se extraen los subconjuntos), ${\displaystyle r}$ (el tamaño de los subconjuntos, como antes) y ${\displaystyle t}$ (el tamaño mínimo de la intersección de dos subconjuntos cualesquiera). Para la forma original del teorema de Erdos-Ko-Rado, ${\displaystyle t=1}$. En general, para ${\displaystyle n}$ suficientemente grande con respecto a los otros dos parámetros, el teorema generalizado establece que el tamaño de una familia de subconjuntos ${\displaystyle t}$-intersecantes está en más de^[25]​ $${\displaystyle {\binom {n-t}{r-t}}.}$$ Más precisamente, este límite se cumple cuando ${\displaystyle n\geq (t+1)(r-t+1)}$, y no se cumple para valores más pequeños de ${\displaystyle n}$. Cuando ${\displaystyle n>(t+1)(r-t+1)}$, las únicas familias {{nowrap|${\displaystyle t}$-intersecantes} de este tamaño se obtienen designando ${\displaystyle t}$ elementos como la intersección común de todos los subconjuntos y construyendo la familia de todos los subconjuntos de ${\displaystyle r}$-elementos que incluyen estos ${\displaystyle t}$ elementos designados.^[26]​ El tamaño máximo de una familia con t elementos intersecantes cuando ${\displaystyle n<(t+1)(r-t+1)}$ fue determinado por Ahlswede y Khachatrian, según el teorema de Ahlswede-Khachatrian.^[27]​

La formulación de la teoría de grafos correspondiente de esta generalización implica un grafo de Johnson en lugar de un grafo^[28]​ de Kneser. Para valores suficientemente grandes de ${\displaystyle n}$, y en particular para ${\displaystyle n>{\tfrac {1}{2}}r^{2}}$, tanto el teorema de Erdos-Ko-Rado como su generalización pueden reforzarse desde el número de independencia hasta la capacidad de Shannon de un grafo: el grafo de Johnson correspondiente a los subconjuntos ${\displaystyle t}$-intersecantes de ${\displaystyle r}$-elementos tiene capacidad de Shannon ${\displaystyle {\tbinom {n-t}{r-t}}}$.^[29]​

El teorema también puede generalizarse a familias en las que todos los ${\displaystyle h}$ subconjuntos tienen una intersección común, porque esto refuerza la condición de que cada par se interseca (para lo cual, ${\displaystyle h=2}$), estas familias tienen la misma cota en su tamaño máximo, ${\displaystyle {\tbinom {n-1}{r-1}}}$, cuando ${\displaystyle n}$ es suficientemente grande). Sin embargo, en este caso, el significado de suficientemente grande puede flexibilizarse de ${\displaystyle n\geq 2r}$ a ${\displaystyle n\geq {\tfrac {h}{h-1}}r}$.^[30]​

Se conocen muchos resultados análogos al teorema de Erdos-Ko-Rado, pero para otras clases de objetos que no sean conjuntos finitos. Estos generalmente implican la afirmación de que las familias más grandes de objetos que se intersecan, para alguna definición de intersección, se obtienen eligiendo un elemento y construyendo la familia de todos los objetos que incluyen ese elemento elegido. Algunos ejemplos incluyen los siguientes:

Existe un q-análogo del teorema de Erdos-Ko-Rado para familias que se intersecan de subespacios vectoriales sobre un cuerpo finito. Si ${\displaystyle {\mathcal {S}}}$ es una familia de subespacios intersecantes ${\displaystyle r}$-dimensionales de un espacio vectorial ${\displaystyle n}$-dimensional sobre un cuerpo finito de orden ${\displaystyle q}$, y ${\displaystyle n\geq 2r}$,, entonces $${\displaystyle |{\mathcal {S}}|\leq {\binom {n-1}{r-1}}_{q},}$$ donde el subíndice q marca la notación para el coeficiente binomial gaussiano, el número de subespacios de una dimensión dada dentro de un espacio vectorial de una dimensión mayor sobre un cuerpo finito de orden q. En este caso, se puede obtener la mayor familia de subespacios intersecantes eligiendo cualquier vector distinto de cero y construyendo la familia de subespacios de la dimensión dada que contengan el vector elegido.^[31]​

Dos permutaciones del mismo conjunto de elementos se definen como intersecantes si existe algún elemento con la misma imagen en ambas permutaciones. En un conjunto de ${\displaystyle n}$-elementos, existe una familia obvia de permutaciones ${\displaystyle (n-1)!}$ intersecantes: las permutaciones que fijan uno de los elementos (la acción de este elemento). El teorema análogo establece que ninguna familia de permutaciones intersecantes puede ser mayor, y que las únicas familias intersecantes de tamaño ${\displaystyle (n-1)!}$ son las clases laterales de estabilizadores de un elemento. Estas pueden describirse más directamente como las familias de permutaciones que asignan un elemento fijo a otro elemento fijo. Más generalmente, para cualquier ${\displaystyle t}$ y ${\displaystyle n}$ suficientemente grande, una familia de permutaciones cada par de las cuales tiene ${\displaystyle t}$ elementos en común tiene tamaño máximo ${\displaystyle (n-t)!}$, y las únicas familias de este tamaño son clases laterales de estabilizadores puntuales.^[32]​

Alternativamente, en términos de la teoría de grafos, las permutaciones de ${\displaystyle n}$-elementos corresponden a las coindidencias perfectas de un grafo bipartito completo ${\displaystyle K_{n,n}}$. El teorema establece que, entre las familias de emparejamientos perfectos cada par de las cuales comparte ${\displaystyle t}$ aristas, las familias más grandes están formadas por los emparejamientos que contienen todos las ${\displaystyle t}$ aristas elegidas.^[33]​

Otro análogo del teorema, para particiones de un conjunto, incluye como un caso especial los emparejamientos perfectos de un grafo completo ${\displaystyle K_{n}}$ (con ${\displaystyle n}$ par). Existen ${\displaystyle (n-1)!!}$ emparejamientos, donde ${\displaystyle !!}$ denota el doble factorial. La familia más grande de emparejamientos que se intersecan por pares (lo que significa que tienen una arista en común) tiene tamaño ${\displaystyle (n-3)!!}$ y se obtiene fijando una arista y eligiendo todas las formas de emparejar los ${\displaystyle n-2}$ vértices restantes. ^[34]​

Una geometría parcial es un sistema de un número finito de puntos y rectas abstractas que satisface ciertos axiomas, incluyendo el requisito de que todas las rectas contengan el mismo número de puntos y todos los puntos pertenezcan al mismo número de rectas. En una geometría parcial, el mayor sistema de rectas que se intersecan por pares se puede obtener del conjunto de rectas mediante cualquier punto.^[35]​

Un conjunto signado consiste en un conjunto con una función de signo que asigna cada elemento a ${\displaystyle \{1,-1\}}$. Se puede decir que dos conjuntos con signo se intersecan cuando tienen un elemento común con el mismo signo. Entonces, una familia de subconjuntos signados de ${\displaystyle r}$-elementos que se intersecan, extraída de un universo de ${\displaystyle n}$-elementos, consiste como máximo en $${\displaystyle 2^{r-1}{\binom {n-1}{r-1}}}$$ subconjuntos signados. Este número de subconjuntos con signo se puede obtener fijando un elemento y su signo, y dejando los elementos y signos ${\displaystyle r-1}$ restantes como variables.^[36]​

Para cadenas de caracteres de longitud ${\displaystyle n}$ sobre un alfabeto de tamaño ${\displaystyle q}$, se pueden definir dos cadenas que se intersecan si tienen una posición donde ambas comparten el mismo símbolo. Las familias de intersección más grandes se obtienen eligiendo una posición y un símbolo fijo para dicha posición, y permitiendo que el resto de las posiciones varíen arbitrariamente. Estas familias consisten en ${\textstyle q^{n-1}}$ subcadenas y son las únicas familias de intersección por pares de este tamaño. De forma más general, las familias de subcadenas más grandes, en las que cada dos tienen ${\displaystyle t}$ posiciones con símbolos iguales, se obtienen eligiendo ${\displaystyle t+2i}$ posiciones y símbolos para dichas posiciones, para un número ${\displaystyle i}$ que depende de ${\displaystyle n}$, ${\displaystyle q}$ y ${\displaystyle t}$, y construyendo la familia de subcadenas que contenga al menos ${\displaystyle t+i}$ de los símbolos elegidos. Estos resultados pueden interpretarse grafoteóricamente en términos del esquema de Hamming.^[37]​

Problemas no resueltos de la matemática: ¿La familia más grande de triangulaciones que se intersecan de un polígono convexo se obtiene cortando un vértice y eligiendo todas las triangulaciones del polígono restante?

Una conjetura no demostrada, planteada por Gil Kalai y Karen Meagher, se refiere a otro análogo para la familia de triangulaciones de un polígono convexo con ${\displaystyle n}$ vértices. El número de todas las triangulaciones es el número de Catalan ${\displaystyle C_{n-2}}$, y la conjetura establece que una familia de triangulaciones cuyos pares comparten una arista tiene un tamaño máximo de ${\displaystyle C_{n-3}}$. Una familia intersecante de tamaño exactamente ${\displaystyle C_{n-3}}$ puede obtenerse cortando un vértice del polígono con un triángulo y eligiendo todas las formas de triangular el polígono restante de ${\displaystyle (n-1)}$-vértices.^[38]​

El teorema de Erdos-Ko-Rado puede utilizarse para demostrar el siguiente resultado en teoría de la probabilidad. Sea ${\displaystyle x_{i}}$ una variable aleatoria 0–1 independiente, con probabilidad ${\displaystyle p\geq {\tfrac {1}{2}}}$ de ser uno, y sea ${\displaystyle c({\vec {x}})}$ cualquier combinación convexa fija de estas variables. Entonces, $${\displaystyle \Pr \left[c({\vec {x}})\geq {\tfrac {1}{2}}\right]\geq p.}$$ La demostración implica observar que los subconjuntos de variables cuyos vectores indicadores tienen combinaciones convexas grandes deben ser no disjuntos y usar el teorema de Erdos-Ko-Rado para limitar el número de estos subconjuntos.^[39]​

Las propiedades de estabilidad del teorema de Erdos-Ko-Rado desempeñan un papel clave en un algoritmo eficiente para encontrar aristas monocromáticas en coloraciones inapropiadas de grafos de Kneser.^[40]​ El teorema de Erdos-Ko-Rado también se ha utilizado para caracterizar las simetrías del espacio de un árbol filogenético.^[41]​

• Teorema de Helly, sobre las condiciones que garantizan que las familias de conjuntos convexos que se intersecan tengan una intersección común.
• Teorema de Sperner, una cota superior para familias de conjuntos no anidados por pares.
• Sistema de Steiner, familias de conjuntos uniformes de tamaño máximo en las que ningún par (en lugar de todos) tiene una intersección grande.
• Girasol (matemáticas), una familia de conjuntos donde (a diferencia de las familias de máxima intersección aquí mostradas) todos los pares tienen intersecciones iguales.
• Thrackle, un problema sin resolver sobre el tamaño de las familias de curvas que se intersecan.

• Cameron, Peter (29 de septiembre de 2017), «EKR, Steiner systems, association schemes, and all that», Peter Cameron's Blog .