Teorema de De Bruijn-Erdős (geometría de incidencia)

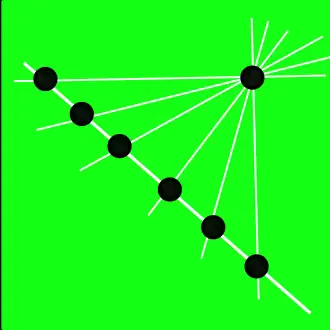
En geometría de incidencia, el teorema de De Bruijn-Erdős, publicado originalmente por Nicolaas Govert de Bruijn y Paul Erdős en 1948,^[1] establece un límite inferior relativo al número de líneas rectas determinado por n puntos en un plano proyectivo. Por la propiedad de la dualidad, esto también constituye una cota respecto al número de puntos de intersección determinado por una configuración de líneas rectas.^[2]

Aunque la demostración de De Bruijn y Erdős es combinatoria, ambos señalaron en su artículo que el resultado análogo (euclídeo) es una consecuencia del teorema de Sylvester-Gallai, mediante una inducción sobre el número de puntos.^[1]

Enunciado del teorema

Sea P una configuración de n puntos en un plano proyectivo, no todos en una recta. Sea t el número de rectas determinado por P. Entonces,

t = n, y
si t = n, dos rectas cualesquiera tienen exactamente un punto de P en común. En este caso, P es un plano proyectivo o P es un casi haz, lo que significa que exactamente n - 1 de los puntos son colineales.^[2]

Demostración euclídea

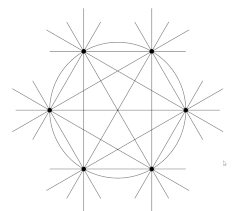
$n$ puntos cocíclicos determinan ${\binom {n}{2}}$ líneas rectas

El teorema es claramente cierto para tres puntos no colineales, y se puede demostrar procediendo por inducción.

Supóngase que n > 3 y que el teorema es cierto para n − 1. Sea P un conjunto de n puntos no todos ellos colineales. El teorema de Sylvester-Gallai establece que existe una recta que contiene exactamente dos puntos de P. Las rectas que contienen únicamente dos puntos se denominan rectas ordinarias. Sean a y b los dos puntos de P de una recta ordinaria. Si la eliminación del punto a produce un conjunto de puntos colineales, entonces P genera un conjunto de n líneas rectas (las n - 1 líneas ordinarias que pasan por a más la línea recta que contiene los otros n - 1 puntos).

De lo contrario, la eliminación de a produce un conjunto, P, de n - 1 puntos que no son todos colineales. Por la hipótesis de inducción, P determina al menos n - 1 líneas rectas. La línea recta ordinaria determinada por a y b no se encuentra entre estas, por lo que P determina al menos n líneas rectas.

Demostración de J. H. Conway

John Horton Conway ideó una demostración puramente combinatoria que, en consecuencia, también es válida para puntos y líneas rectas sobre los números complejos, cuaterniones y octoniones.^[3]

Referencias

↑ ^a ^b De Bruijn, N. G.; Erdős, P. (1948), «On a combinatioral [sic] problem», Indagationes Mathematicae 10: 421-423 .
↑ ^a ^b Batten, Lynn Margaret (1997), «2.2 The De Bruijn–Erdős theorem», Combinatorics of Finite Geometries (2nd edición), Cambridge University Press, pp. 25–27, ISBN 0-521-59014-0 .
↑ Stasys Jukna, Extremal Combinatorics, Second edition, Springer Verlag, 2011, pages 167 - 168.

Datos: Q3527056

[dbe-1] De Bruijn, N. G.; Erdős, P. (1948), «On a combinatioral [sic] problem», Indagationes Mathematicae 10: 421-423 .

[batten-2] Batten, Lynn Margaret (1997), «2.2 The De Bruijn–Erdős theorem», Combinatorics of Finite Geometries (2nd edición), Cambridge University Press, pp. 25–27, ISBN 0-521-59014-0 .

[3] Stasys Jukna, Extremal Combinatorics, Second edition, Springer Verlag, 2011, pages 167 - 168.

[1]

[2]

[3]