Inecuación

Una inecuación (escritura derivada del latín "in" (no) y "aequatio" (igualación)) es una desigualdad algebraica en la cual los conjuntos (miembros) se encuentran relacionados por los signos ${\displaystyle <}$ (menor que), ${\displaystyle \leq }$ (menor o igual que), ${\displaystyle >}$ (mayor que) y ${\displaystyle \geq }$ (mayor o igual que). Por ejemplo:

${\displaystyle 2x<2}$ o ${\displaystyle 3x-2<9}$

Estas expresiones algebraicas son inecuaciones siempre y cuando las variables tomen valores que satisfagan la desigualdad.

Del mismo modo en que se hace la diferencia entre igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las que son válidas solo para algunos valores de las variables se conocen como inecuaciones condicionales.^[1]​ Los valores que verifican la desigualdad, son sus soluciones.

• Ejemplo de inecuación incondicional: ${\displaystyle |x|\leq |x|+|y|}$.
• Ejemplo de inecuación condicional: ${\displaystyle -2x+7<2}$.

Los criterios más comunes de clasificación del ejemplo: ${\displaystyle x<0}$.

• De dos incógnitas. Ejemplo: ${\displaystyle x<y}$.
• De tres incógnitas. Ejemplo: ${\displaystyle x<y+z}$.
• etc.

Según la potencia de la incógnita,

• De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: ${\displaystyle x+1<0}$.
• De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: ${\displaystyle x^{2}+1<0}$.
• De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: x^3 + 1 < 0.

• etc.

Se expresan a través de cualquiera de las desigualdades siguientes (con a, b y c números reales, y a distinto de cero):

• ${\displaystyle ax^{2}+bx+c<0}$
• ${\displaystyle ax^{2}+bx+c\leq 0}$
• ${\displaystyle ax^{2}+bx+c>0}$
• ${\displaystyle ax^{2}+bx+c\geq 0}$
• ${\displaystyle a\neq 0}$

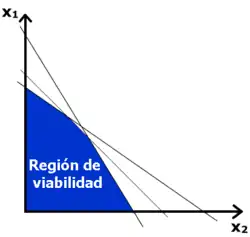
En un sistema de inecuaciones intervienen dos o más inecuaciones. No todos los sistemas de inecuaciones tienen solución.

Es un conjunto de inecuaciones de primer grado

${\displaystyle \left\{{\begin{array}{rcrcrcr}ax+b<0\\cx+d\geq 0\\...\\lx+m>0\\\end{array}}\right.}$

La solución del sistema será el conjunto de números reales que verifican a la vez todas las inecuaciones.

Luego del origen de las ecuaciones, surgió las inecuaciones tras el gradual desarrollo de las ecuaciones probablemente en la Antigua Grecia entre los años "1700aC. - 1700dC." debido al surgimiento de un problema que contenía como solución un conjunto de números que podían ser expresados a través de una inecuación (x>k)^[2]​. En esos tiempos los antiguos matemáticos griegos exploraban la relación y la comparación de los números con variables, buscando los valores de la variable que cumplan la desigualdad.

Luego, el matemático Diofanto de Alejandría introdujo el uso de incógnitas auxiliares al momento de resolver ecuaciones cuadráticas con la finalidad de reducir los problemas a ecuaciones lineales junto a desigualdades. En donde las desigualdades servían para reducir y especificar las soluciones de la ecuación.

Con el paso del tiempo se empezó a formalizarse el concepto de una inecuación y a establecerse signos para representar una desigualdad de dos cantidades. Cuyo objetivo de su desarrollo fue para resolver, comprender y para representar problemas que tuvieran un conjunto de soluciones que se podían representar a través de la desigualdad de una incógnita y una cantidad.

• Ecuación
• Desigualdad matemática
• Sistema de ecuaciones
• Sistema de ecuaciones lineales
• Programación lineal

• Casteleiro Villalba, José Manuel (2008). La matemática es fácil. Esic. ISBN 978-84-7356-533-2. 
• Del Pozo García, Eva María (2004). Matemáticas fundamentales para estudios universitarios. Pearson Educación. ISBN 84-933631-6-2. 
• Fleming, Walter & Dale Varberg (1991). Álgebra y trigonometría con geometría analítica. Delta Publicaciones. ISBN 968-880-222-0. 
• González García, Carlos (2008). Matemáticas 1° Bachillerato. Editex.