Simulación de grandes remolinos

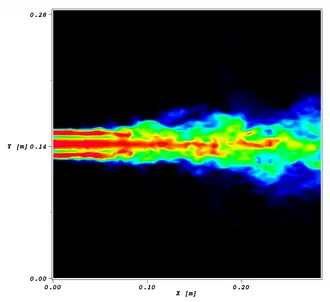
La simulación de grandes remolinos (LES, por sus siglas en inglés) es un modelo matemático para la turbulencia utilizado en la dinámica de fluidos computacional. Fue propuesto inicialmente en 1963 por Joseph Smagorinsky para simular las corrientes de aire atmosférico,^[1]​ y explorado por primera vez por Deardorff (1970).^[2]​ Actualmente, la LES se aplica en una amplia variedad de aplicaciones de ingeniería, incluida la combustión,^[3]​ acústica,^[4]​ y simulaciones de la capa límite atmosférica.^[5]​

La simulación de flujos turbulentos mediante la resolución numérica de las ecuaciones de Navier-Stokes requiere resolver una amplia gama de escalas de tiempo y longitud, todas las cuales afectan al campo de flujo. Esta resolución se puede lograr con la simulación numérica directa (DNS), pero la DNS es computacionalmente costosa y su coste impide la simulación de sistemas de ingeniería prácticos con geometrías o configuraciones de flujo complejas, como chorros turbulentos, bombas, vehículos y trenes de aterrizaje.

La idea principal detrás de la LES es reducir el coste computacional ignorando las escalas de longitud más pequeñas, que son las más costosas de resolver, mediante el filtrado de paso bajo de las ecuaciones de Navier-Stokes. Este filtrado de paso bajo, que puede considerarse como un promedio temporal y espacial, elimina eficazmente la información a pequeña escala de la solución numérica. Sin embargo, esta información no es irrelevante y su efecto sobre el campo de flujo debe modelarse, una tarea que es un área activa de investigación para problemas en los que las pequeñas escalas pueden desempeñar un papel importante, como los flujos cercanos a las paredes,^[6]​^[7]​ flujos reactivos,^[3]​ y flujos multifásicos.^[8]​

Se puede aplicar un filtro LES a un campo espacial y temporal ${\displaystyle \phi ({\boldsymbol {x}},t)}$ y realizar una operación de filtrado espacial, una operación de filtrado temporal o ambas. El campo filtrado, denotado con una barra, se define como:^[9]​^[10]​

${\displaystyle {\overline {\phi ({\boldsymbol {x}},t)}}=\displaystyle {\int _{-\infty }^{\infty }}\int _{-\infty }^{\infty }\phi ({\boldsymbol {r}},\tau )G({\boldsymbol {x}}-{\boldsymbol {r}},t-\tau )d\tau d{\boldsymbol {r}}}$

donde ${\displaystyle G}$ es el núcleo de convolución del filtro. Esto también se puede escribir como:

${\displaystyle {\overline {\phi }}=G\star \phi .}$

El núcleo del filtro ${\displaystyle G}$ tiene una escala de corte asociada ${\displaystyle \Delta }$ y una escala de tiempo de corte ${\displaystyle \tau _{c}}$. Las escalas menores que estas se eliminan de ${\displaystyle {\overline {\phi }}}$. Utilizando la definición de filtro anterior, cualquier campo ${\displaystyle \phi }$ puede dividirse en una parte filtrada y otra subfiltrada (denotada con un apóstrofo), como

${\displaystyle \phi ={\bar {\phi }}+\phi ^{\prime }.}$

Es importante señalar que la operación de filtrado de simulación de grandes remolinos no satisface las propiedades de un Operador de Reynolds.

Las ecuaciones determinantes de LES se obtienen filtrando las ecuaciones diferenciales parciales que determinan el campo de flujo ${\displaystyle \rho {\boldsymbol {u}}({\boldsymbol {x}},t)}$. Existen diferencias entre las ecuaciones determinantes LES incompresibles y compresibles, lo que lleva a la definición de una nueva operación de filtrado.

Para el flujo incompresible, se filtran la ecuación de continuidad y las ecuaciones de Navier-Stokes, lo que da como resultado la ecuación de continuidad incompresible filtrada,

${\displaystyle {\frac {\partial {\bar {u_{i}}}}{\partial x_{i}}}=0}$

y las ecuaciones de Navier-Stokes filtradas,

${\displaystyle {\frac {\partial {\bar {u_{i}}}}{\partial t}}+{\frac {\partial }{\partial x_{j}}}\left({\overline {u_{i}u_{j}}}\right)=-{\frac {1}{\rho }}{\frac {\partial {\overline {p}}}{\partial x_{i}}}+\nu {\frac {\partial }{\partial x_{j}}}\left({\frac {\partial {\bar {u_{i}}}}{\partial x_{j}}}+{\frac {\partial {\bar {u_{j}}}}{\partial x_{i}}}\right)=-{\frac {1}{\rho }}{\frac {\partial {\overline {p}}}{\partial x_{i}}}+2\nu {\frac {\partial }{\partial x_{j}}}{\bar {S}}_{ij},}$

donde ${\displaystyle {\bar {p}}}$ es el campo de presión filtrado y ${\displaystyle {\bar {S}}_{ij}}$ es el tensor de velocidad de deformación evaluado utilizando la velocidad filtrada. El término de advección filtrado no lineal ${\displaystyle {\overline {u_{i}u_{j}}}}$ es la principal causa de dificultad en el modelado LES. Requiere conocer el campo de velocidad sin filtrar, que se desconoce, por lo que debe modelarse. El análisis que sigue ilustra la dificultad causada por la no linealidad, es decir, que provoca una interacción entre escalas grandes y pequeñas, lo que impide la separación de escalas.

El término de advección filtrado puede dividirse, siguiendo a Leonard (1975),^[11]​ como:

${\displaystyle {\overline {u_{i}u_{j}}}=\tau _{ij}+{\overline {u}}_{i}{\overline {u}}_{j}}$

donde ${\displaystyle \tau _{ij}}$ es el tensor de tensión residual, de modo que las ecuaciones de Navier-Stokes filtradas se convierten en

${\displaystyle {\frac {\partial {\bar {u_{i}}}}{\partial t}}+{\frac {\partial }{\partial x_{j}}}\left({\overline {u}}_{i}{\overline {u}}_{j}\right)=-{\frac {1}{\rho }}{\frac {\partial {\overline {p}}}{\partial x_{i}}}+2\nu {\frac {\partial }{\partial x_{j}}}{\bar {S}}_{ij}-{\frac {\partial \tau _{ij}}{\partial x_{j}}}}$

con el tensor de tensión residual ${\displaystyle \tau _{ij}}$ agrupando todos los términos no cerrados. Leonard descompuso este tensor de tensión como ${\displaystyle \tau _{ij}=L_{ij}+C_{ij}+R_{ij}}$ y proporcionó interpretaciones físicas para cada término. ${\displaystyle L_{ij}={\overline {{\bar {u}}_{i}{\bar {u}}_{j}}}-{\bar {u}}_{i}{\bar {u}}_{j}}$, el tensor de Leonard, representa las interacciones entre grandes escalas, ${\displaystyle R_{ij}={\overline {u_{i}^{\prime }u_{j}^{\prime }}}}$, el término similar a la tensión de Reynolds, representa las interacciones entre las subescalas del filtro (SFS), y ${\displaystyle C_{ij}={\overline {{\bar {u}}_{i}u_{j}^{\prime }}}+{\overline {{\bar {u}}_{j}u_{i}^{\prime }}}}$, el tensor de Clark,^[12]​ representa las interacciones entre escalas grandes y pequeñas.^[11]​ Modelar el término no cerrado ${\displaystyle \tau _{ij}}$ es la tarea de los modelos de escala sub-grid (SGS). Esto resulta complicado debido a que el tensor de tensión subgrid ${\displaystyle \tau _{ij}}$ debe tener en cuenta las interacciones entre todas las escalas, incluidas las escalas filtradas con escalas no filtradas.

La ecuación determinante filtrada para un escalar pasivo ${\displaystyle \phi }$, como la fracción de mezcla o la temperatura, se puede escribir como

${\displaystyle {\frac {\partial {\overline {\phi }}}{\partial t}}+{\frac {\partial }{\partial x_{j}}}\left({\overline {u}}_{j}{\overline {\phi }}\right)={\frac {\partial {\overline {J_{\phi }}}}{\partial x_{j}}}+{\frac {\partial q_{j}}{\partial x_{j}}}}$

donde ${\displaystyle J_{\phi }}$ es el flujo difusivo de ${\displaystyle \phi }$, y ${\displaystyle q_{j}}$ es el flujo subfiltrado para el escalar ${\displaystyle \phi }$. El flujo difusivo filtrado ${\displaystyle {\overline {J_{\phi }}}}$ no está cerrado, a menos que se le asuma una forma particular, como un modelo de difusión gradiente ${\displaystyle J_{\phi }=D_{\phi }{\frac {\partial \phi }{\partial x_{i}}}}$. ${\displaystyle q_{j}}$ se define de forma análoga a ${\displaystyle \tau _{ij}}$,

${\displaystyle q_{j}={\bar {\phi }}{\overline {u}}_{j}-{\overline {\phi u_{j}}}}$

y puede dividirse de forma similar en contribuciones de interacciones entre varias escalas. Este flujo de subfiltro también requiere un modelo de subfiltro.

Utilizando la notación de Einstein, las ecuaciones de Navier-Stokes para un fluido incompresible en coordenadas cartesianas son

${\displaystyle {\frac {\partial u_{i}}{\partial x_{i}}}=0}$

${\displaystyle {\frac {\partial u_{i}}{\partial t}}+{\frac {\partial u_{i}u_{j}}{\partial x_{j}}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial x_{i}}}+\nu {\frac {\partial ^{2}u_{i}}{\partial x_{j}\partial x_{j}}}.}$

Filtrando la ecuación del momento se obtiene

${\displaystyle {\overline {\frac {\partial u_{i}}{\partial t}}}+{\overline {\frac {\partial u_{i}u_{j}}{\partial x_{j}}}}=-{\overline {{\frac {1}{\rho }}{\frac {\partial p}{\partial x_{i}}}}}+{\overline {\nu {\frac {\partial ^{2}u_{i}}{\partial x_{j}\partial x_{j}}}}}.}$

Si suponemos que el filtrado y la diferenciación son conmutativos, entonces

${\displaystyle {\frac {\partial {\bar {u_{i}}}}{\partial t}}+{\overline {\frac {\partial u_{i}u_{j}}{\partial x_{j}}}}=-{\frac {1}{\rho }}{\frac {\partial {\bar {p}}}{\partial x_{i}}}+\nu {\frac {\partial ^{2}{\bar {u_{i}}}}{\partial x_{j}\partial x_{j}}}.}$