Salvo (matemáticas)

En matemáticas, el término salvo o a menos de (o módulo en contextos informales) indica que el objeto al que se refiere debe ser considerado como una clase de equivalencia. Por ejemplo, diremos que a y b son iguales salvo una relación de equivalencia R si a y b, aun pudiendo no ser iguales, están relacionados por R (pertenecen a la misma clase de equivalencia). Nótese que en este contexto, la expresón «salvo» no tiene un sentido de excepción o de exclusión, sino por el contrario, de inclusión o equivalencia.

La relación de equivalencia R normalmente no se menciona explícitamente, sino que se usa una "condición o transformación que la genera": si X es un proceso o propiedad, el término "salvo X" debe entenderse como "descartando una posible diferencia en X".

Por ejemplo, la expresión "la factorización en factores primos de un entero es única salvo reordenaciones" quiere decir que la factorización es única si no tenemos en cuenta el orden de los factores o, más explícitamente, que cualesquiera dos listas de factores primos de un entero deben estar relacionadas por la relación de equivalencia R que relaciona dos listas si son reordenación (permutación) la una de la otra.

Como otro ejemplo, la expresión "la solución de una integral indefinida es ${\displaystyle \sin(x)}$ salvo sumar una constante" significa que la solución es ${\displaystyle \sin(x)}$ pero también cualquier otra función que se obtenga sumándole a ${\displaystyle \sin(x)}$ una constante, o lo que es lo mismo, cualquier función f(x) relacionada con ${\displaystyle \sin(x)}$ por la relación de equivalencia ${\displaystyle fRg}$ si ${\displaystyle g(x)=f(x)+c}$, con ${\displaystyle c}$ una constante.

En contextos informales, los matemáticos suelen utilizar la palabra módulo para propósitos similares: "la factorización en números primos de un entero es única módulo permutación de los factores", "la integral indefinida es única módulo suma de constante", "hay dos grupos de orden 4 módulo isomorfismo", etc.

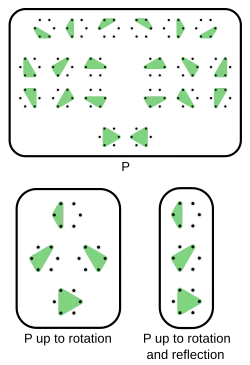
Consideremos las ocho piezas del Tetris (I, J, L, O, S, T, Z), que se conocen en matemáticas como tetrominós. Si consideramos todas las posibles rotaciones de estas (por ejemplo, si consideramos la I en vertical distinta de la I en horizontal) veríamos que hay hasta 19 opciones. Es decir, podríamos decir que hay 19 tetrominós. Pero no consideramos distintos dos tetrominós que sean rotación el uno del otro, entonces hay sólo 7. Diremos que "hay 7 tetrominós salvo/módulo rotación". Esta es la información relevante para el Tetris, pues el juego nos permite rotar las piezas. Sin embargo, también podríamos considerar iguales dos tetrominós que difirieran por una simetría: "los tetrominós J y el L son iguales salvo/módulo simetría", "los tetrominós S y Z son iguales salvo/mósulo simetría", "hay 5 tetrominós módulo rotación y simetría".

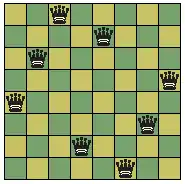
En el problema de las ocho reinas se nos pide colocar ocho reinas en un tablero de ajedrez sin que se amenacen las unas a las otras. Si las reinas se consideraran todas distintas (por ejemplo, si estuvieran pintadas de distintos colores), entonces tendríamos 3709440 soluciones distintas. Sin embargo, normalmente consideramos que las reinas son intercambiables, y normalmente decimos que hay "${\displaystyle 3709440/8!=92}$ soluciones salvo permutación de las reinas", con lo que queremos decir que dos colocaciones de las reinas los consideramos iguales aunque hayamos intercambiado la posición de dos reinas, siempre y cuando ocupen las mismas casillas del tablero.

Si además de tratar todas las reinas como iguales, también permitimos rotaciones y simetrías del tablero, sólo tendremos 12 soluciones "salvo permutación de las reinas y rotaciones y simetrías del tablero".

Para más información sobre el problema, léase Problema de las ocho reinas.

El teorema fundamental de la aritmética enuncia que ‘‘todo número natural se puede descomponer en producto de factores primos de forma única salvo reordenación/permutación de los factores’’, es decir, que dos factorizaciones sólo pueden diferir por el orden en que ponen los factores.

En teoría de grupos podemos considerar un grupo G actuando sobre un conjunto X (transformando unos elementos de X en otros, con unas ciertas propiedades). En ese caso, se puede decir que dos elementos de X son "iguales salvo acción de G" si pertenecen a la misma órbita (si podemos transformar uno en el otro por el grupo G).

Otro ejemplo típico es la afirmación " hay dos grupos de orden 4 salvo isomorfismo". Esto significa que si consideramos como iguales dos grupos que sean isomorfos, sólo hay dos grupos con cuatro elementos.

Uno de los resultados más importantes de la topología es el de clasificar las superficies compactas (intuitivamente, que están no se extienden infinitamente y "no tienen borde") y conexas salvo homeomorfismo (intuitivamente, un homeomorfismo es una "deformación de un espacio en otro sin romperlo ni pegar trozos que no estuvieran pegados"), es decir, dar una lista de superficies de manera que cualquier otra sea igual salvo homeomorfismo a alguna de la lista, que se pueda deformar en alguna de la lista.

El resultado es que toda superficie compacta y conexa es homeomorfa a una esfera, a la suma conexa de n toros para algún n (una superficie con n agujeros, n toros "engachados") o a la suma conexa de n planos proyectivos para algún n (n planos proyectivos "enganchados"). Si descartamos las superficies no orientables, podemos descartar los planos proyectivos. Podemos decir pues que, módulo homeomorfismo, las únicas superficies compactas, conexas y orientables son la esfera y la suma conexa de n toros; toda superficie compacta conexa orientable se puede deformar en una esfera o en una superficie con n agujeros.

• 
  Esfera
• 
  Toro
• 
  Suma conexa de dos toros
• 
  Suma conexa de tres toros

• Salvo orden de los factores (véase propiedad conmutativa)
• Salvo isomorfismo
• Salvo simetría
• Salvo permutación
• Salvo traslación
• Salvo orientación
• Salvo afinidad
• Salvo semejanza

• Aritmética modular
• Teoría de grupos

• Nachbin, Leopoldo (1980). Introducción al álgebra. Reverté SA. p. 76. ISBN 84-291--5099-4. 
• Castelet, Manuel, Llerena, Irene (1996). Álgebra lineal y geometría. Reverté. ISBN 84-291-5009-9. 
• «up to». wiktionary (en inglés).