Ráfagas continuas

Las ráfagas continuas o ráfagas estocásticas son vientos que varían aleatoriamente en el espacio y el tiempo. Los modelos de ráfagas continuas se utilizan para representar la turbulencia atmosférica, especialmente la turbulencia en aire claro y los vientos turbulentos en las tormentas. La Administración Federal de Aviación (FAA) y el Departamento de Defensa de los Estados Unidos establecen los requisitos para los modelos de ráfagas continuas utilizados en el diseño y la simulación de aeronaves.^[1]​^[2]​

Existen diversos modelos para las ráfagas^[3]​, pero solo dos, los modelos Dryden y von Kármán, se utilizan generalmente para las ráfagas continuas en aplicaciones de dinámica de vuelo.^[2]​ ^[4]​ Ambos modelos definen las ráfagas en términos de densidades espectrales de potencia para los componentes de velocidad lineal y angular parametrizados por escalas de longitud e intensidades de turbulencia. Los componentes de velocidad de estos modelos de ráfagas continuas pueden incorporarse a las ecuaciones de movimiento de los aviones como perturbaciones del viento.^[5]​ Aunque estos modelos de ráfagas continuas no son ruido blanco, se pueden diseñar filtros que tomen una entrada de ruido blanco y produzcan un proceso aleatorio con los modelos Dryden o von Kármán.^[6]​^[7]​

Los modelos aceptados por la FAA y el Departamento de Defensa representan las ráfagas continuas como un campo de velocidad lineal y angular del viento que es un proceso aleatorio y hacen una serie de supuestos simplificadores para describirlos matemáticamente. En particular, se supone que las ráfagas continuas son:^[8]​

• Un proceso gaussiano
• Un proceso estacionario, por lo que las estadísticas son constantes en el tiempo
• Homogéneo, por lo que las estadísticas no dependen de la trayectoria del vehículo
• Ergódico
• Isotrópico a gran altitud, por lo que las estadísticas no dependen de la actitud del vehículo
• Variable en el espacio pero congelado en el tiempo

Estas suposiciones, aunque poco realistas, dan lugar a modelos aceptables para aplicaciones de dinámica de vuelo.^[9]​ La última suposición de un campo de velocidad que no varía con el tiempo es especialmente poco realista, ya que las mediciones de la turbulencia atmosférica en un punto del espacio siempre varían con el tiempo. Estos modelos se basan en el movimiento del avión a través de las ráfagas para generar variaciones temporales en la velocidad del viento, lo que los hace inadecuados para su uso como entradas en modelos de vuelo estacionario, turbinas eólicas u otras aplicaciones fijas en el espacio.

Los modelos también hacen suposiciones sobre cómo varían las ráfagas continuas con la altitud. Los modelos Dryden y von Kármán especificados por el Departamento de Defensa definen tres rangos de altitud diferentes: baja, de 10 a 1000 pies AGL; media/alta, 2000 pies AGL y superior; y entremedias. Las intensidades de la turbulencia, las longitudes de la escala de la turbulencia y los ejes de la turbulencia dependen de la altitud.^[10]​ El Departamento de Defensa también proporciona modelos para la velocidad angular de las ráfagas, pero ofrece criterios basados en las derivadas de estabilidad de los aviones para determinar cuándo pueden omitirse.^[11]​

El modelo Dryden es uno de los modelos más utilizados para las ráfagas continuas. Se publicó por primera vez en 1952.^[12]​ La densidad espectral de potencia del componente de velocidad lineal longitudinal es

${\displaystyle \Phi _{u_{g}}(\Omega )=\sigma _{u}^{2}{\frac {2L_{u}}{\pi }}{\frac {1}{1+(L_{u}\Omega )^{2}}}}$

donde u_g es el componente de velocidad lineal longitudinal de las ráfagas, σ_u es la intensidad de la turbulencia, L_u es la longitud de la escala de la turbulencia y Ω es una frecuencia espacial.^[2]​

El modelo Dryden tiene densidades espectrales de potencia racionales para cada componente de velocidad. Esto significa que se puede formar un filtro exacto que toma ruido blanco como entrada y produce un proceso aleatorio con las densidades espectrales de potencia del modelo Dryden. ^[6]​

El modelo de von Kármán es el modelo preferido de ráfagas continuas para el Departamento de Defensa y la FAA.^[1]​^[2]​ El modelo apareció por primera vez en un informe de 1957 del NACA^[13]​ basado en trabajos anteriores de Theodore von Kármán.^[14]​^[15]​^[16]​ En este modelo, la densidad espectral de potencia del componente de velocidad lineal longitudinal es

${\displaystyle \Phi _{u_{g}}(\Omega )=\sigma _{u}^{2}{\frac {2L_{u}}{\pi }}{\frac {1}{\left(1+(1.339L_{u}\Omega )^{2}\right)^{\frac {5}{6}}}}}$

donde u_g es el componente de velocidad lineal longitudinal, σ_u es la intensidad de la turbulencia, L_u es la longitud de la escala de la turbulencia y Ω es una frecuencia espacial.^[2]​

El modelo de von Kármán tiene densidades espectrales de potencia irracionales. Por lo tanto, un filtro con una entrada de ruido blanco que genera un proceso aleatorio con las densidades espectrales de potencia del modelo de von Kármán solo puede aproximarse.^[7]​

Tanto el modelo Dryden como el von Kármán se parametrizan mediante una escala de longitud y una intensidad de turbulencia. La combinación de estos dos parámetros determina la forma de las densidades espectrales de potencia y, por lo tanto, la calidad del ajuste de los modelos a los espectros de turbulencia observados. Muchas combinaciones de escala de longitud e intensidad de turbulencia dan densidades espectrales de potencia realistas en los rangos de frecuencia deseados.^[4]​ Las especificaciones del Departamento de Defensa incluyen opciones para ambos parámetros, incluida su dependencia de la altitud, que se resumen a continuación.^[10]​

La baja altitud se define como las altitudes comprendidas entre 10 pies AGL y 1000 pies AGL.

A baja altitud, las longitudes de escala son funciones de la altitud,

${\displaystyle 2L_{w}=h}$

${\displaystyle L_{u}=2L_{v}={\frac {h}{(0.177+0.000823h)^{1.2}}}}$ donde «h» es la altitud AGL. A 1000 pies AGL, «L_u» = 2«L_v» = 2«L_w» = 1000 pies.

A baja altitud, las intensidades de turbulencia se parametrizan mediante «W»₂₀, la velocidad del viento a 20 pies.

Turbulencia severa	${\displaystyle W_{20}}$
Baja	15 kts
Moderada	30 kts
Severa	45 kts

${\displaystyle \sigma _{w}=0.1W_{20}}$

${\displaystyle {\frac {\sigma _{u}}{\sigma _{w}}}={\frac {\sigma _{v}}{\sigma _{w}}}={\frac {1}{(0.177+0.000823h)^{0.4}}}}$

A 1000 ft AGL,

${\displaystyle \sigma _{u}=\sigma _{v}=\sigma _{w}=0.1W_{20}}$

La altitud media/alta se define como 2000 pies AGL y superior.

Para el modelo Dryden, ${\displaystyle L_{u}=2L_{v}=2L_{w}=1750{\text{ft}}}$

Para el modelo de von Kármán,

${\displaystyle L_{u}=2L_{v}=2L_{w}=2500{\text{ft}}}$

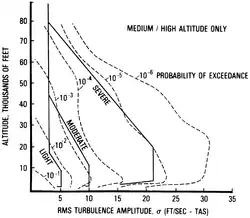
A gran altitud,

${\displaystyle \sigma _{u}=\sigma _{v}=\sigma _{w}}$

Se parametrizan mediante la probabilidad de superación o la gravedad de la turbulencia. En las especificaciones militares se proporciona un gráfico de la intensidad de la turbulencia en función de la altitud, en el que se muestran líneas de probabilidad de superación constante y rangos correspondientes a diferentes gravedades de turbulencia.^[17]​

Desde 1000 pies AGL hasta 2000 pies AGL, tanto la escala de longitud como la intensidad de la turbulencia se determinan mediante interpolación lineal entre el valor de baja altitud a 1000 pies y el valor de altitud media/alta a 2000 pies.^[6]​^[7]​

Por encima de 1750 pies, los ejes de la turbulencia coinciden con los ejes del sistema de referencia del viento. Por debajo de 1750 pies, el eje vertical de la turbulencia se alinea con el sistema de referencia terrestre El eje «z», el eje longitudinal de la turbulencia, está alineado con la proyección del vector del viento medio sobre el plano horizontal del marco terrestre, y el eje lateral de la turbulencia viene determinado por la regla de la mano derecha.^[18]​

• Turbulencia en aire claro
• Modelo de turbulencia eólica de Dryden
• Modelo de turbulencia eólica de von Kármán

• Etkin, Bernard (2005). Dynamics of Atmospheric Flight. Mineola, NY: Dover Publications. ISBN 0486445224. 
• Hoblit, Frederic M. (1988). Gust Loads on Aircraft: Concepts and Applications. Washington, DC: American institute of Aeronautics and Astronautics, Inc. ISBN 0930403452. 
• Flying Qualities of Piloted Aircraft. MIL-STD-1797A. United States Department of Defense. 1990.