Problema del triángulo de Heilbronn

En geometría discreta y teoría de la discrepancia, el problema del triángulo de Heilbronn es un problema de colocación de puntos en el plano, evitando triángulos de área pequeña. Lleva el nombre de Hans Heilbronn, quien conjetura que, sin importar cómo se coloquen los puntos en un área dada, el área del triángulo más pequeño será a lo sumo inversamente proporcional al cuadrado del número de puntos. Su conjetura fue refutada, pero la tasa de crecimiento asintótico del área mínima del triángulo sigue siendo desconocida.

El problema del triángulo de Heilbronn se centra en la colocación de ${\displaystyle n}$ puntos dentro de una forma en el plano, como el cuadrado unitario o el disco unitario, para un número dado ${\displaystyle n}$. Cada trío de puntos forma los tres vértices de un triángulo, y entre estos triángulos, el problema se interesa por el triángulo más pequeño, medido por su área. Diferentes disposiciones de puntos tendrán diferentes triángulos más pequeños, y el problema pregunta: ¿cómo deben colocarse ${\displaystyle n}$ puntos para maximizar el área del triángulo más pequeño?^[1]​

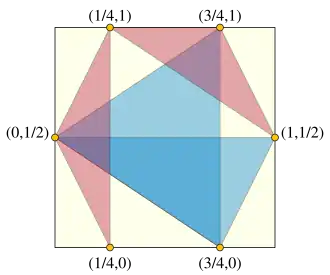
Más formalmente, la forma puede asumirse como un conjunto compacto ${\displaystyle D}$ en el plano, lo que significa que permanece dentro de una distancia acotada desde el origen y que los puntos pueden colocarse en su frontera. En la mayoría de los trabajos sobre este problema, ${\displaystyle D}$ es además un conjunto convexo de área no nula. Cuando tres de los puntos colocados están en una línea, se consideran como formadores de un triángulo degenerado cuya área se define como cero, por lo que las disposiciones que maximizan el triángulo más pequeño no tendrán tríos de puntos colineales. La suposición de que la forma es compacta implica que existe una colocación óptima de ${\displaystyle n}$ puntos, en lugar de solo una secuencia de colocaciones que se aproximan a la optimalidad. El número ${\displaystyle \Delta _{D}(n)}$ puede definirse como el área del triángulo más pequeño en esta colocación óptima.^[1]​^[2]​ Un ejemplo se muestra en la figura, con seis puntos en un cuadrado unitario. Estos seis puntos forman ${\displaystyle {\tbinom {6}{3}}=20}$ triángulos diferentes, cuatro de los cuales están sombreados en la figura. Seis de estos 20 triángulos, con dos de las formas sombreadas, tienen un área de 1/8; los 14 triángulos restantes tienen áreas mayores. Esta es la colocación óptima de seis puntos en un cuadrado unitario: todas las demás colocaciones forman al menos un triángulo con área 1/8 o menor. Por lo tanto, ${\displaystyle \Delta _{D}(6)={\tfrac {1}{8}}}$.^[3]​

Aunque los investigadores han estudiado el valor de ${\displaystyle \Delta _{D}(n)}$ para formas específicas y números pequeños de puntos,^[3]​^[4]​^[5]​ Heilbronn estaba más interesado en su comportamiento asintótico: si la forma ${\displaystyle D}$ se mantiene fija, pero ${\displaystyle n}$ varía, ¿cómo varía el área del triángulo más pequeño con ${\displaystyle n}$? Es decir, la pregunta de Heilbronn se refiere a la tasa de crecimiento de ${\displaystyle \Delta _{D}(n)}$, como función de ${\displaystyle n}$. Para dos formas cualesquiera ${\displaystyle D}$ y ${\displaystyle D'}$, los números ${\displaystyle \Delta _{D}(n)}$ y ${\displaystyle \Delta _{D'}(n)}$ difieren solo por un factor constante, ya que cualquier colocación de ${\displaystyle n}$ puntos dentro de ${\displaystyle D}$ puede escalarse mediante una transformación afín para encajar dentro de ${\displaystyle D'}$, cambiando el área del triángulo mínimo solo por una constante. Por lo tanto, en los límites de la tasa de crecimiento de ${\displaystyle \Delta _{D}(n)}$ que omiten la constante de proporcionalidad de ese crecimiento, la elección de ${\displaystyle D}$ es irrelevante y el subíndice puede omitirse.^[1]​

Heilbronn conjeturó antes de 1951 que el área del triángulo mínimo siempre se reduce rápidamente como función de ${\displaystyle n}$—más específicamente, inversamente proporcional al cuadrado de ${\displaystyle n}$.^[1]​^[6]​ En términos de la notación O grande, esto puede expresarse como el límite $${\displaystyle \Delta (n)=O\left({\frac {1}{n^{2}}}\right).}$$

En la otra dirección, Paul Erdős encontró ejemplos de conjuntos de puntos con un área de triángulo mínima proporcional a ${\displaystyle 1/n^{2}}$, demostrando que, si es cierta, la conjetura de Heilbronn no podía reforzarse. Erdős formuló el problema de no tres en línea, sobre grandes conjuntos de puntos en una rejilla sin tres en línea, para describir estos ejemplos. Como observó Erdős, cuando ${\displaystyle n}$ es un número primo, el conjunto de ${\displaystyle n}$ puntos ${\displaystyle (i,i^{2}{\bmod {n}})}$ en una rejilla entera ${\displaystyle n\times n}$ (para ${\displaystyle 0\leq i<n}$) no tienen tres puntos colineales, y por lo tanto, según la fórmula de Pick, cada uno de los triángulos que forman tiene un área de al menos ${\displaystyle {\tfrac {1}{2}}}$. Cuando estos puntos de la rejilla se escalan para encajar en un cuadrado unitario, su área de triángulo más pequeña es proporcional a ${\displaystyle 1/n^{2}}$, coincidiendo con el límite superior conjeturado por Heilbronn. Si ${\displaystyle n}$ no es primo, entonces una construcción similar usando un número primo cercano a ${\displaystyle n}$ logra el mismo límite inferior asintótico.^[1]​^[7]​}

Komlós, Pintz y Szemerédi (1982) finalmente refutaron la conjetura de Heilbronn, utilizando el método probabilístico para encontrar conjuntos de puntos cuya área de triángulo más pequeña es mayor que las encontradas por Erdős. Su construcción involucra los siguientes pasos:

• Colocar aleatoriamente ${\displaystyle n^{1+\varepsilon }}$ puntos en el cuadrado unitario, para algún ${\displaystyle \varepsilon >0}$.
• Eliminar todos los pares de puntos que estén inesperadamente cerca uno del otro.
• Demostrar que hay pocos triángulos de área baja y, por lo tanto, solo un número sublineal de ciclos formados por dos, tres o cuatro triángulos de área baja. Eliminar todos los puntos que pertenezcan a estos ciclos.
• Aplicar un lema de eliminación de triángulos para hipergrafos uniformes de 3 con alta circunferencia para mostrar que, con alta probabilidad, los puntos restantes incluyen un subconjunto de ${\displaystyle n}$ puntos que no forman triángulos de área pequeña.

El área resultante de su construcción crece asintóticamente como^[8]​ $${\displaystyle \Delta (n)=\Omega \left({\frac {\log n}{n^{2}}}\right).}$$ La prueba puede ser desaleatorizada, lo que lleva a un algoritmo de tiempo polinómico para construir colocaciones con esta área de triángulo.^[9]​

Cada conjunto de ${\displaystyle n}$ puntos en el cuadrado unitario forma un triángulo de área a lo sumo inversamente proporcional a ${\displaystyle n}$. Una forma de verlo es triangular la envoltura convexa del conjunto de puntos dado ${\displaystyle S}$, y elegir el más pequeño de los triángulos en la triangulación. Otra es ordenar los puntos por sus coordenadas ${\displaystyle x}$, y elegir los tres puntos consecutivos en este orden cuyas coordenadas ${\displaystyle x}$ estén más cerca. En el primer artículo publicado sobre el problema del triángulo de Heilbronn, en 1951, Klaus Roth demostró un límite superior más fuerte en ${\displaystyle \Delta (n)}$, de la forma^[1]​ $${\displaystyle \Delta (n)=O\left({\frac {1}{n{\sqrt {\log \log n}}}}\right).}$$ El mejor límite conocido hasta la fecha es de la forma $${\displaystyle \Delta (n)\leq {\frac {\exp {\left(c{\sqrt {\log n}}\right)}}{n^{8/7}}},}$$ para alguna constante ${\displaystyle c}$, demostrado por Komlós, Pintz y Szemerédi (1981).^[10]​

Un nuevo límite superior igual a ${\displaystyle n^{-{\frac {8}{7}}-{\frac {1}{2000}}}}$ fue demostrado por Cohen, Pohoata y Zakharov (2023).^[11]​^[12]​

Goldberg (1972) ha investigado las disposiciones óptimas de ${\displaystyle n}$ puntos en un cuadrado, para ${\displaystyle n}$ hasta 16.^[3]​ Las construcciones de Goldberg para hasta seis puntos se encuentran en la frontera del cuadrado y están colocadas para formar una transformación afín de los vértices de un polígono regular. Para valores mayores de ${\displaystyle n}$, Comellas y Yebra (2002) mejoraron los límites de Goldberg, y para estos valores las soluciones incluyen puntos interiores al cuadrado.^[4]​ Estas construcciones han sido demostradas óptimas para hasta siete puntos. La prueba utilizó una búsqueda computacional para subdividir el espacio de configuración de posibles disposiciones de los puntos en 226 subproblemas diferentes, y utilizó técnicas de programación no lineal para mostrar que en 225 de esos casos, la mejor disposición no era tan buena como el límite conocido. En el caso restante, que incluye la solución óptima final, su optimalidad fue demostrada usando técnicas de cálculo simbólico.^[5]​

Las siguientes son las mejores soluciones conocidas para 7–12 puntos en un cuadrado unitario, encontradas mediante recocido simulado;^[4]​ la disposición para siete puntos se sabe que es óptima.^[5]​

• 
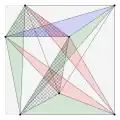  7 puntos en un cuadrado, todos los 8 triángulos mínimos sombreados (${\displaystyle A\approx 0.0839}$)
• 
  8 puntos en un cuadrado, 5 de 12 triángulos mínimos sombreados^[13]​ (${\displaystyle A\approx 0.0724}$)
• 
  9 puntos en un cuadrado, 6 de 11 triángulos mínimos sombreados^[13]​ (${\displaystyle A\approx 0.0549}$)
• 
  10 puntos en un cuadrado, 3 de 16 triángulos mínimos sombreados^[13]​ (${\displaystyle A\approx 0.0465}$)
• 
  11 puntos en un cuadrado, 8 de 28 triángulos mínimos sombreados^[13]​ (${\displaystyle A\approx 0.0370}$)
• 
  12 puntos en un cuadrado, 3 de 20 triángulos mínimos sombreados^[13]​ (${\displaystyle A\approx 0.0326}$)

En lugar de buscar colocaciones óptimas para una forma dada, se puede buscar una forma óptima para un número dado de puntos. Entre las formas convexas ${\displaystyle D}$ con área uno, el hexágono regular es el que maximiza ${\displaystyle \Delta _{D}(6)}$; para esta forma, ${\displaystyle \Delta _{D}(6)={\tfrac {1}{6}}}$, con seis puntos colocados óptimamente en los vértices del hexágono.^[14]​ Las formas convexas de área unitaria que maximizan ${\displaystyle \Delta _{D}(7)}$ tienen ${\displaystyle \Delta _{D}(7)={\tfrac {1}{9}}}$.^[15]​

Se han estudiado muchas variaciones de este problema, incluido el caso de un conjunto de puntos distribuidos uniformemente al azar, para el cual argumentos basados en la complejidad de Kolmogorov o la aproximación de Poisson muestran que el valor esperado del área mínima es inversamente proporcional al cubo del número de puntos.^[16]​^[17]​ También se han estudiado variaciones que involucran el volumen de símplices de dimensiones superiores.^[18]​^[19]​^[20]​

Otra versión de dimensión superior añade otro parámetro ${\displaystyle k}$, y pregunta por colocaciones de ${\displaystyle n}$ puntos en el hipercubo unitario que maximicen el volumen mínimo de la envoltura convexa de cualquier subconjunto de ${\displaystyle k}$ puntos. Para ${\displaystyle k=d+1}$, estos subconjuntos forman símplices, pero para valores mayores de ${\displaystyle k}$, relativos a ${\displaystyle d}$, pueden formar formas más complicadas. Cuando ${\displaystyle k}$ es suficientemente grande en relación con ${\displaystyle \log n}$, los conjuntos de puntos colocados aleatoriamente tienen un volumen de envoltura convexa mínimo de ${\displaystyle k}$-puntos ${\displaystyle \Omega (k/n)}$. No es posible un límite mejor; cualquier colocación tiene ${\displaystyle k}$ puntos con volumen ${\displaystyle O(k/n)}$, obtenido al elegir algunos ${\displaystyle k}$ puntos consecutivos en orden de coordenadas. Este resultado tiene aplicaciones en estructuras de datos de búsqueda por rangos.^[21]​

• Weisstein, Eric W. «Heilbronn Triangle Problem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Centro de empaquetamiento de Erich, por Erich Friedman, incluye las mejores soluciones conocidas para el problema de Heilbronn para valores pequeños de ${\displaystyle n}$ en cuadrados, círculos, triángulos equiláteros y regiones convexas de forma variable pero área fija.