Problema del recubrimiento de un disco

Problemas no resueltos de la matemática: ¿Cuál es el número real más pequeño ${\displaystyle r(n)}$ tal que ${\displaystyle n}$ discos de radio ${\displaystyle r(n)}$ se puedan disponer de tal manera que recubran el disco unitario?

El problema del recubrimiento de un disco consiste en determinar el número real ${\displaystyle r(n)}$ más pequeño tal que ${\displaystyle n}$ discos de radio ${\displaystyle r(n)}$ puedan disponerse de forma que recubran el disco unidad. Dualmente, para un radio dado µ, se busca el entero n más pequeño tal que n discos de radio µ puedan recubrir el disco unidad.^[1]​

Las mejores soluciones conocidas hasta la fecha son las siguientes:^[2]​

n	r(n)	Simetrías
1	1	Todas
2	1	Todas (2 discos apilados)
3	${\displaystyle {\sqrt {3}}/2}$= 0.866025...	120°, 3 reflexiones
4	${\displaystyle {\sqrt {2}}/2}$= 0.707107...	90°, 4 reflexiones
5	0.609382... A133077	1 reflexión
6	0.555905... A299695	1 reflexión
7	${\displaystyle 1/2}$= 0.5	60°, 6 reflexiones
8	0.445041...	~51.4°, 7 reflexiones
9	0.414213...	45°, 8 reflexiones
10	0.394930...	36°, 9 reflexiones
11	0.380083...	1 reflexión
12	0.361141...	120°, 3 reflexiones

La siguiente imagen muestra un ejemplo de un disco (con trazo discontinuo) de radio 1, recubierto por seis discos (con línea continua) de radio ~0,6. Uno de los discos de cobertura se coloca centralmente y los cinco restantes de forma simétrica a su alrededor.

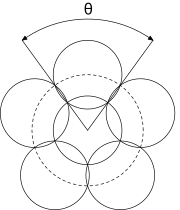
Si bien esta no es la mejor disposición para r(6), disposiciones similares de seis, siete, ocho y nueve discos alrededor de un disco central, todos con el mismo radio, son las mejores estrategias de disposición para r(7), r(8), r(9) y r(10), respectivamente.^[2]​ Los ángulos θ correspondientes se indican en la columna "Simetría" de la tabla anterior.

• Weisstein, Eric W. «Disk Covering Problem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Finch, S. R. "Constantes de Cobertura Circular". §2.2 en Constantes Matemáticas. Cambridge, Inglaterra: Cambridge University Press, págs. 484–489, 2003.