Problema de la fábrica de ladrillos de Turán

En las matemáticas del dibujo de grafos, el problema de la fábrica de ladrillos de Turán plantea el número mínimo de cruces en el dibujo de un grafo bipartito completo. El problema debe su nombre a Pál Turán, que lo formuló mientras se veía obligado a trabajar en una fábrica de ladrillos durante la Segunda Guerra Mundial.^[1]​

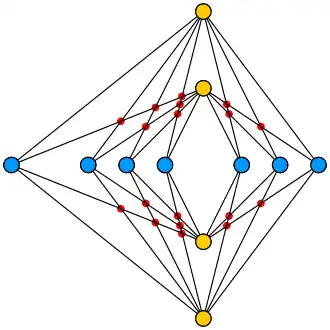
Se ha conjeturado que un método de dibujo encontrado por Kazimierz Zarankiewicz da la respuesta correcta para cada grafo bipartito completo, y la afirmación de que esto es cierto se conoce como la conjetura del número de cruce de Zarankiewicz. La conjetura sigue abierta y sólo se han resuelto algunos casos especiales.^[2]​

Durante la Segunda Guerra Mundial, el matemático húngaro Pál Turán fue obligado a trabajar en una fábrica de ladrillos, empujando vagones cargados de ladrillos desde los hornos hasta los almacenes. La fábrica tenía vías desde cada horno hasta cada lugar de almacenamiento, y los vagones eran más difíciles de empujar en los puntos donde las vías se cruzaban. Esta situación inspiró a Turán a preguntarse cómo podría rediseñarse la fábrica para minimizar el número de cruces entre estas vías.^[1]​

Desde el punto de vista matemático, este problema se puede formalizar pidiendo el dibujo de un grafo bipartito completo, cuyos vértices representen hornos y lugares de almacenamiento, y cuyas aristas representen las vías desde cada horno hasta cada lugar de almacenamiento. El gráfico debe dibujarse en el plano, con cada vértice como un punto, cada arista como una curva que une sus dos extremos y ningún vértice situado en una arista con la que no esté en contacto. Se cuenta un cruce siempre que dos aristas que son disjuntas en el gráfico tienen una intersección no vacía en el plano. La pregunta es entonces, ¿cuál es el número mínimo de cruces en un dibujo de este tipo?^[2]​^[3]​

La formulación de Turán de este problema se reconoce a menudo como uno de los primeros estudios de los números de cruce de los grafos.^[4]​ (Otra formulación independiente del mismo concepto se produjo en sociología, en los métodos para dibujar sociogramas,^[5]​ y un enigma mucho más antiguo, el problema de las tres utilidades, puede verse como un caso especial del problema de la fábrica de ladrillos con tres hornos y tres almacenes).^[6]​ Desde entonces, los números de cruce han adquirido mayor importancia, como objeto central de estudio en el dibujo de grafos^[7]​ y como herramienta importante en el diseño VLSI^[8]​ y la geometría discreta.^[9]​

Tanto Zarankiewicz como Kazimierz Urbanik vieron a Turán hablar del problema de la fábrica de ladrillos en diferentes charlas en Polonia en 1952,^[3]​ y publicaron independientemente intentos de solución del problema, con fórmulas equivalentes para el número de cruces.^[10]​^[11]​ Como ambos demostraron, siempre es posible dibujar el grafo bipartito completo ${\displaystyle Km,n}$ (un grafo con ${\displaystyle n}$ vértices en un lado, ${\displaystyle n}$ vértices en el otro y ${\displaystyle mn}$ aristas que conectan ambos lados) con un número de cruces igual a:

${\displaystyle \operatorname {cr} (K_{m,n})\leq {\biggl \lfloor }{\frac {n}{2}}{\biggr \rfloor }{\biggl \lfloor }{\frac {n-1}{2}}{\biggr \rfloor }{\biggl \lfloor }{\frac {m}{2}}{\biggr \rfloor }{\biggl \lfloor }{\frac {m-1}{2}}{\biggr \rfloor }.}$

La construcción es sencilla: coloca ${\displaystyle m}$ vértices en el eje ${\displaystyle x}$ del plano, evitando el origen, con un número igual o casi igual de puntos a la izquierda y a la derecha del eje ${\displaystyle y}$. Del mismo modo, coloca n vértices en el eje y del plano, evitando el origen, con un número igual o casi igual de puntos por encima y por debajo del eje x. Del mismo modo, coloca n vértices en el eje y del plano, evitando el origen, con un número igual o casi igual de puntos por encima y por debajo del eje x. A continuación, conecte cada punto del eje x mediante un segmento de línea recta con cada punto del eje y.^[3]​

Sin embargo, sus pruebas de que esta fórmula es óptima, es decir, que no puede haber dibujos con menos cruces, eran erróneas. La laguna no se descubrió hasta once años después de la publicación, casi simultáneamente por Gerhard Ringel y Paul Kainen.^[12]​ No obstante, se conjetura que la fórmula de Zarankiewicz y Urbanik es óptima. Esto se conoce como la conjetura del número de cruce de Zarankiewicz. Aunque se sabe que algunos casos especiales son ciertos, el caso general sigue abierto.^[2]​

Dado que ${\displaystyle K(m,n)}$ y ${\displaystyle K(n,m)}$ son isomorfos, basta con considerar el caso en que m ≤ n. Además, para m ≤ 2 la construcción de Zarankiewicz no da cruces, lo que por supuesto no puede superarse. Así que los únicos casos no triviales son aquellos para los que ${\displaystyle m}$ y ${\displaystyle n}$ son ambos ≥ 3.

El intento de prueba de la conjetura de Zarankiewicz, aunque inválido para el caso general de ${\displaystyle K(m,n)}$ funciona para el caso ${\displaystyle m}$ = 3. Desde entonces se ha extendido a otros valores pequeños de m, y se sabe que la conjetura de Zarankiewicz es cierta para los grafos bipartitos completos ${\displaystyle K(m,n)}$ con ${\displaystyle m}$ ≤ 6.^[13]​ También se sabe que la conjetura es cierta para K_7,7, K_7,8, y K_7,9.^[14]​ Si existe un contraejemplo, es decir, un grafo ${\displaystyle K(m,n)}$ que requiere menos cruces que el límite de Zarankiewicz, entonces en el contraejemplo más pequeño tanto m como n deben ser impares.^[13]​

Para cada elección fija de m, la verdad de la conjetura para todo ${\displaystyle K(m,n)}$ puede verificarse probando sólo un número finito de opciones de ${\displaystyle n}$.^[15]​ En términos más generales, se ha demostrado que todo grafo bipartito completo requiere un número de cruces que es (para grafos suficientemente grandes) al menos el 83% del número dado por el límite de Zarankiewicz. Cerrar la brecha entre este límite inferior y el superior sigue siendo un problema abierto.^[16]​

Si se requiere que las aristas se dibujen como segmentos de líneas rectas, en lugar de curvas arbitrarias, entonces algunos grafos necesitan más cruces de los que necesitarían si se dibujaran con aristas curvas. Sin embargo, el límite superior establecido por Zarankiewicz para el número de cruces de grafos bipartitos completos puede alcanzarse utilizando sólo aristas rectas. Por lo tanto, si la conjetura de Zarankiewicz es correcta, entonces los grafos bipartitos completos tienen números de cruce rectilíneos iguales a sus números de cruce.^[17]​

• Weisstein, Eric W., «Conjetura de Zarankiewicz», MathWorld