Polígono cóncavo

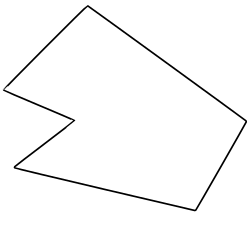
Un polígono simple se llama cóncavo si tiene un lado que al alargarlo lo parte.^[1]​ Un polígono cóncavo tiene al menos un ángulo interior midiendo más de 180 grados ( ${\displaystyle \pi }$ radianes).

• Ángulo entrante: es el ángulo cuya medida es mayor que 180°
• Diagonal: Cualquier segmento que une dos vértices no consecutivos.
• Desde el vértice de un ángulo entrante es posible una descomposición en figuras convexas de menor número de lado, si es posible en triángulos.
• Punto interior: Es aquel punto que es interior a uno de polígonos convexos que resulta de una descomposición, mediante una diagonal o diagonales que parten del vértice de un ángulo entrante.........

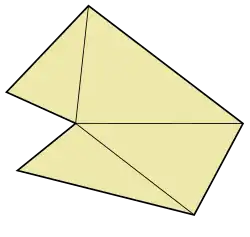
• Por cada ángulo entrante hay al menos una diagonal que contiene puntos del exterior del polígono, excepto sus extremos.
• Un polígono cóncavo de ${\displaystyle n}$ vértices, de los cuales solo uno es entrante, admite una al menos una Triangulación en abanico en ${\displaystyle n-2}$ triángulos trazando diagonales desde el vértice entrante.
• Un polígono cóncavo de ${\displaystyle n}$ lados puede tener a lo sumo una cantidad de ángulos entrantes a lo sumo igual a ${\displaystyle n/2}$.
• Cualquier polígono cóncavo tiene, por lo menos, dos lados, tal que la prolongación de cualquiera de ellos determina dos semiplanos y divide al polígono en dos partes, de modo que cada semiplano contiene solo una de las dos partes del polígono.

Ligando con la geometría computacional, es posible optimizar o situar un punto o más en la región poligonal, que permitan una mayor vigilancia del ambiente cuyo contorno es un polígono cóncavo.

Shashkin Yu: Característica euleriana.Editorial Mir, Moscú, 1989, traducción revisada y ampliada al español. Traductor del ruso: B. Mirchevski; impreso en La URSS.
Geometría computacional, edición de IMCA, Lima.
Geometría plana de Estrada y Sánchez.

• Polígono convexo
• Polígono
• Polígono estrellado
• Interior
• Exterior

• Diccionario de Materias: Polígono cóncavo