Numeración Kaktovik

La numeración Kaktovik o numeración Kaktovik Iñupiaq[1] es un sistema de dígitos numéricos de base 20 creado por los inupiat de Alaska. Estos dígitos son visualmente icónicos, ya que sus formas reflejan el valor numérico que representan.
El idioma iñupiaq utiliza un sistema numérico de base 20, al igual que otras lenguas esquimo-aleutianas de Alaska, Canadá y, en el pasado, Groenlandia. Los números arábigos, diseñados para un sistema de base 10, resultan insuficientes para representar los números en iñupiaq y otras lenguas inuit. Para solucionar este inconveniente, en 1994, estudiantes de Kaktovik (Alaska), inventaron una notación numérica de base 20 que se ha difundido entre los inupiat de Alaska y se ha considerado para su uso en Canadá.
Sistema
El iñupiaq, al igual que otras lenguas inuit, emplea un sistema de conteo de base 20 con una subbase de 5 (un sistema quinario-vigesimal). Esto significa que las cantidades se cuentan en grupos de veinte (similar a los galeses o al francés quatre-vingts "ochenta"), con numerales intermedios para 5, 10 y 15. Por ejemplo, el número 78 se expresa como tres veintes quince-tres.[2]
Los dígitos Kaktovik reflejan gráficamente la estructura léxica del sistema numérico iñupiaq.[3]
| 0 | kisitchisaġvik | 5 | tallimat | 10 | qulit | 15 | akimiaq | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | atausiq | 6 | itchaksrat | 11 | qulit atausiq | 16 | akimiaq atausiq | ||||
| 2 | malġuk | 7 | tallimat malġuk | 12 | qulit malġuk | 17 | akimiaq malġuk | ||||
| 3 | piŋasut | 8 | tallimat piŋasut | 13 | qulit piŋasut | 18 | akimiaq piŋasut | ||||
| 4 | sisamat | 9 | quliŋŋuġutaiḷaq | 14 | akimiaġutaiḷaq | 19 | iñuiññaġutaiḷaq |
Los números mayores se forman combinando estos dígitos en una notación posicional:
| Decimal | Vigesimal | |
|---|---|---|
| Arábigos | Arábigos | Kaktovik |
| 20 | 1020 | |
| 40 | 2020 | |
| 400 | 10020 | |
| 800 | 20020 | |
Valores
En la siguiente tabla se presentan los valores decimales de los dígitos Kaktovik hasta tres posiciones a la izquierda y a la derecha del lugar de las unidades.[3]
| n | n × 203 | n × 202 | n × 201 | n × 200 | n × 20−1 | n × 20−2 | n × 20−3 |
|---|---|---|---|---|---|---|---|
| 1 | 8,000 |
400 |
20 |
1 |
0.05 |
0.0025 |
0.000125 |
| 2 | 16,000 |
800 |
40 |
2 |
0.1 |
0.005 |
0.00025 |
| 3 | 24,000 |
1,200 |
60 |
3 |
0.15 |
0.0075 |
0.000375 |
| 4 | 32,000 |
1,600 |
80 |
4 |
0.2 |
0.01 |
0.0005 |
| 5 | 40,000 |
2,000 |
100 |
5 |
0.25 |
0.0125 |
0.000625 |
| 6 | 48,000 |
2,400 |
120 |
6 |
0.3 |
0.015 |
0.00075 |
| 7 | 56,000 |
2,800 |
140 |
7 |
0.35 |
0.0175 |
0.000875 |
| 8 | 64,000 |
3,200 |
160 |
8 |
0.4 |
0.02 |
0.001 |
| 9 | 72,000 |
3,600 |
180 |
9 |
0.45 |
0.0225 |
0.001125 |
| 10 | 80,000 |
4,000 |
200 |
10 |
0.5 |
0.025 |
0.00125 |
| 11 | 88,000 |
4,400 |
220 |
11 |
0.55 |
0.0275 |
0.001375 |
| 12 | 96,000 |
4,800 |
240 |
12 |
0.6 |
0.03 |
0.0015 |
| 13 | 104,000 |
5,200 |
260 |
13 |
0.65 |
0.0325 |
0.001625 |
| 14 | 112,000 |
5,600 |
280 |
14 |
0.7 |
0.035 |
0.00175 |
| 15 | 120,000 |
6,000 |
300 |
15 |
0.75 |
0.0375 |
0.001875 |
| 16 | 128,000 |
6,400 |
320 |
16 |
0.8 |
0.04 |
0.002 |
| 17 | 136,000 |
6,800 |
340 |
17 |
0.85 |
0.0425 |
0.002125 |
| 18 | 144,000 |
7,200 |
360 |
18 |
0.9 |
0.045 |
0.00225 |
| 19 | 152,000 |
7,600 |
380 |
19 |
0.95 |
0.0475 |
0.002375 |
Origen
Los números Kaktovik surgieron en 1994 como una actividad de enriquecimiento durante una clase de matemáticas sobre números binarios en la escuela secundaria Harold Kaveolook, ubicada en la isla Barter, Kaktovik (Alaska).[4] Los estudiantes notaron que su idioma empleaba un sistema de base 20.
Al intentar escribir números o realizar operaciones aritméticas con números arábigos, descubrieron que no contaban con suficientes símbolos para representar los números iñupiaq.[5] Inicialmente, crearon diez símbolos adicionales, pero estos resultaron difíciles de memorizar. La pequeña escuela, con solo nueve estudiantes, permitió que todos trabajaran juntos en la creación de una notación de base 20, guiados por su profesor, William Bartley.[5]
Tras una lluvia de ideas, los estudiantes definieron varias características que un sistema ideal debería tener:
- Simplicidad visual: Los símbolos debían ser "fáciles de recordar".
- Iconicidad: Debía existir una "relación clara entre los símbolos y sus significados".
- Eficiencia: Los símbolos debían ser "fáciles de escribir" y poder trazarse rápidamente sin levantar el lápiz del papel.
- Distinción: Debían "diferenciarse claramente de los números arábigos" para evitar confusiones entre ambos sistemas.
- Estética: Tenían que ser agradables a la vista.[5]
En la notación posicional de base 20, el número veinte se escribe con el dígito 1 seguido del dígito 0. Como el idioma iñupiaq no tiene una palabra para cero, los estudiantes decidieron que el dígito 0 de Kaktovik se asemejaría a brazos cruzados, indicando que no se estaba contando nada.[5]
Cuando los estudiantes de secundaria comenzaron a enseñar este sistema a los alumnos más jóvenes, estos últimos tendían a comprimir los números para que encajaran en bloques del mismo tamaño. Así, crearon una notación icónica en la que la subbase de 5 forma la parte superior del dígito y el resto la parte inferior, lo que resultó útil visualmente para realizar operaciones aritméticas.[5]
Cómputo

Ábaco
Los estudiantes construyeron ábacos de base 20 en el taller de la escuela.[4][5] Inicialmente, estos se diseñaron para facilitar la conversión entre decimal y base 20, pero los estudiantes descubrieron que su diseño se adaptaba naturalmente a la aritmética de base 20. La sección superior del ábaco tenía tres cuentas por columna para los valores de la subbase de 5, y la sección inferior tenía cuatro cuentas por columna para las unidades restantes.[5]
Aritmética
Los estudiantes encontraron que una ventaja de su nuevo sistema era que la aritmética resultaba más sencilla que con los números arábigos.[5] Al sumar dos dígitos, el resultado se parecía visualmente a su suma. Por ejemplo:
- 2 + 2 = 4
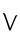 +
+ 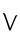 =
= 
La resta era aún más simple: bastaba con observar el número y eliminar la cantidad adecuada de trazos para obtener la respuesta.[5] Por ejemplo:
- 4 − 1 = 3
 −
− 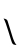 =
= 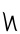
Otra ventaja se manifestó en la división larga. Los aspectos visuales y la subbase de 5 hacían que la división larga con dividendos grandes fuera casi tan fácil como la división corta, ya que no requería anotar subtareas de multiplicación y sustracción en pasos intermedios.[4] Los estudiantes podían seguir los trazos de los pasos intermedios con lápices de colores en un sistema elaborado de segmentación.[5]
División larga simple
.svg.png)
30,56110 ÷ 6110 = 50110
3,G8120 ÷ 3120 = 15120
![]()
![]()
![]()
![]() ÷
÷ ![]()
![]() =
=![]()
![]()
![]()
- Negro: El divisor
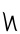
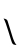 entra una vez en los dos primeros dígitos del dividendo, para un
entra una vez en los dos primeros dígitos del dividendo, para un 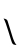 uno en el cociente.
uno en el cociente. - Rojo:
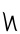
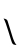 cabe en los dos dígitos siguientes una vez (si está girado), por lo que el siguiente dígito del cociente es un uno girado (es decir, un
cabe en los dos dígitos siguientes una vez (si está girado), por lo que el siguiente dígito del cociente es un uno girado (es decir, un cinco).
cinco). - Azul: Los dos últimos dígitos coinciden una vez para un
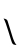 uno final en el cociente.
uno final en el cociente.
División larga más fragmentada
.svg.png)
46,349,22610 ÷ 2,82610 = 16,40110
E9D,D1620 ÷ 71620 = 2,10120
![]()
![]()
![]()
![]()
![]()
![]() ÷
÷ ![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
Negro y rojo: El divisor ![]()
![]()
![]() entra en los tres primeros dígitos del dividendo dos veces (una en negro y otra en rojo), para un dos en el cociente.
entra en los tres primeros dígitos del dividendo dos veces (una en negro y otra en rojo), para un dos en el cociente.
- Azul:
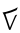
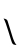
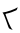 entra una vez en los tres dígitos siguientes, por un
entra una vez en los tres dígitos siguientes, por un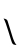 uno en el cociente.
uno en el cociente. - Gris:
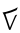
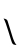
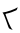 no cabe en los tres dígitos siguientes, por un
no cabe en los tres dígitos siguientes, por un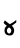 cero en el cociente.
cero en el cociente. - Verde:
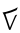
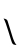
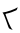 encaja en los dígitos restantes una vez, para un
encaja en los dígitos restantes una vez, para un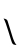 uno final en el cociente.
uno final en el cociente.
Tabla de multiplicación
Se puede crear una tabla de multiplicación simplificada encontrando primero los productos de cada dígito base, luego los productos de las bases y subbases, y finalmente el producto de cada subbase:
| × | 1 |
2 |
3 |
4 |
| 1 |
||||
| 2 |
||||
| 3 |
||||
| 4 |
| × | 1 |
2 |
3 |
4 |
| 5 |
||||
| 10 |
||||
| 15 |
| × | 5 |
10 |
15 |
| 5 |
|||
| 10 |
|||
| 15 |
Estas tablas son funcionalmente completas para operaciones de multiplicación con números Kaktovik, pero para factores con bases y subbases es necesario descomponerlos primero:
- 6 * 3 = 18
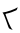 *
* 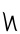 = (
= ( 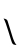 *
* 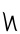 ) + (
) + (  *
* 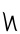 ) =
) = 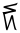
En el ejemplo anterior, el factor ![]() (6) no está en la tabla, pero sus componentes,
(6) no está en la tabla, pero sus componentes, ![]() (1) y
(1) y ![]() (5), sí lo están.
(5), sí lo están.
Legado
Los números Kaktovik han ganado un uso amplio entre los inupiat de Alaska. Se han incorporado a programas de inmersión lingüística y han contribuido a revitalizar el conteo de base 20, que estaba cayendo en desuso debido a la predominancia del sistema de base 10 en las escuelas de habla inglesa.[4][5]
Cuando los estudiantes de la escuela secundaria de Kaktovik que inventaron el sistema se graduaron y pasaron a la escuela secundaria en Barrow (Alaska) (ahora renombrada Utqiaġvik), en 1995, llevaron su invención consigo. Se les permitió enseñarlo a los estudiantes de la escuela secundaria local, y el colegio comunitario Iḷisaġvik College añadió un curso de matemáticas inuit a su catálogo.[5]
En 1996, la Comisión de Historia, Lengua y Cultura Inuit adoptó oficialmente los números,[5] y en 1998, el Consejo Circumpolar Inuit en Canadá recomendó el desarrollo y uso de los números Kaktovik en ese país.[6]
Significado
Las puntuaciones en el California Achievement Test de matemáticas en la escuela secundaria de Kaktovik mejoraron notablemente en 1997 en comparación con años anteriores. Antes de la introducción de los nuevos números, el promedio estaba en el percentil 20; tras su implementación, las puntuaciones superaron el promedio nacional. Se teoriza que trabajar de base 10 y base 20 podría ofrecer ventajas similares a las que tienen los estudiantes bilingües al emplear dos formas de pensar sobre el mundo.[5]
El desarrollo de un sistema numérico indígena demuestra a los estudiantes nativos de Alaska que las matemáticas están integradas en su cultura y lengua, en lugar de ser algo impuesto por la cultura occidental. Esto cambia la percepción previa de que las matemáticas eran solo una necesidad para ingresar a una universidad. Los estudiantes no nativos pueden ver un ejemplo práctico de una visión del mundo diferente, parte de la etnomatemática.[7]
En Unicode
Los números Kaktovik fueron añadidos al estándar Unicode en septiembre de 2022, con el lanzamiento de la versión 15.0. Varias fuentes son compatibles con este bloque
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| U+1D2Cx | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 | 𝋃 |
| U+1D2Dx | 𝋃 | 𝋃 | 𝋃 | 𝋃 | ||||||||||||
| Notas
1. A partir de la versión 16.0 de la norma Unicode | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| U+1D2Cx | ||||||||||||||||
| U+1D2Dx |
Véase también
- Numeración maya, un sistema quinario-vigesimal de otra cultura americana
Referencias
Bibliografía
- Bartley, Wm. Clark (1 de enero de 1997). «Making the Old Way Count». Sharing Our Pathways (en inglés) 2 (1): 12-13. Archivado desde el original el 25 de junio de 2013. Consultado el 27 de febrero de 2017.
- «Resolution 89-09: Regarding Kaktovik Numerals». Inuit Circumpolar Conference (en inglés) (Nuuk (Groenlandia)). Julio de 1998. Archivado desde el original el 2 de febrero de 2017.
- Bartley, William Clark (2002). «Counting on tradition: Iñupiaq numbers in the school setting». En Elaine Hankes, Judith; Fast, Gerald R., eds. Perspectives on Indigenous People of North America. Changing the Faces of Mathematics (en inglés). Reston (Virginia): National Council of Teachers of Mathematics. pp. 225-236. ISBN 978-0873535069. Consultado el 17 de abril de 2024.
- Engblom-Bradley, Claudette (2009). Williams, Maria Sháa Tláa, ed. The Alaska Native Reader: History, Culture, Politics (en inglés). Duke University Press. pp. 237-245. ISBN 978-0-8223-4465-0. doi:10.1215/9780822390831-025.
- MacLean, Edna Ahgeak (1 de enero de 2012). Iñupiatun Uqaluit Taniktun Sivunniuġutiŋit [Diccionario del iñupiaq del North Slope al inglés] (en inglés). Archivado desde el original el 10 de diciembre de 2021.
- MacLean, Edna Ahgeak (1 de enero de 2014). Iñupiatun Uqaluit Taniktun Sivuninit [Diccionario del iñupiaq al inglés] (en inglés). University of Alaska Press.
Lecturas complementarias
- Tillinghast-Raby, Amory (junio de 2023). «A Number System Invented by Inuit Schoolchildren Will Make Its Silicon Valley Debut». Scientific American Magazine (en inglés). Consultado el 13 de abril de 2023.
Enlaces externos
- Convertidor Kaktovik–Arábigo, usando imágenes o Unicode (en inglés)
- Grunewald, Edgar (30 de diciembre de 2019). «Why These Are The Best Numbers!». YouTube (en inglés). Archivado desde el original el 20 de diciembre de 2021. El video demuestra cómo la división larga es más fácil con dígitos visualmente intuitivos como los de Kaktovik; los problemas ilustrados fueron elegidos para resolverse fácilmente, como en una introducción infantil a la aritmética.
- Silva, Eduardo Marín; Miller, Kirk; Strand, Catherine (29 de abril de 2021). «Unicode request for Kaktovik numerals (L2/21-058R)». Unicode Technical Committee Document Registry (en inglés). Consultado el 30 de abril de 2021.
- Aplicación gratuita Calculadora Kaktovik, en iPhone (1 de diciembre de 2023). (en inglés)