Mínimo común múltiplo

En matemáticas, el mínimo común múltiplo (mcm o m. c. m.) de dos o más números naturales es el menor múltiplo común de todos ellos. Este concepto está ligado a las fracciones de números naturales, pero se puede aplicar también a los enteros negativos y los números complejos. El mínimo común múltiplo es el número menor de los múltiplos comunes. Por ejemplo, si los múltiplos comunes de 2 y 3 son 6,12,18..., el mínimo común múltiplo -o mcm- es 6, ya que es el menor de los múltiplos comunes de 2 y 3.

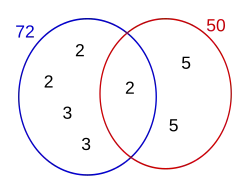
Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar todos los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será

Tomando los factores con su mayor exponente, tenemos que:

${\displaystyle \operatorname {MCM} (72,50)=2^{3}\cdot 3^{2}\cdot 5^{2}=1800}$

Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.

${\displaystyle \operatorname {mcm} (a,b)={\frac {a\cdot b}{\operatorname {MCD} (a,b)}}}$

1. Si a es un entero, ${\displaystyle mcm(a,a)=a}$. En general, ${\displaystyle |mcm(a,b)|\geq |a|}$
2. ${\displaystyle mcm(a,b)=mcm(b,a)}$, propiedad conmutativa
3. ${\displaystyle mcm(a,b)=b\iff a\mid b}$, el mínimo común múltiplo de un número y un divisor es él mismo.
4. ${\displaystyle mcm(a,b)=MCD(a,b)\iff |a|=|b|}$
5. ${\displaystyle mcm(a,b)=ab\iff MCD(a,b)=1}$, el mínimo común múltiplo de dos números es su producto si, y solo si, a y b son primos entre sí.
6. ${\displaystyle MCD(mcm(a,b)/a,x)=1\implies mcm(x\cdot a,b)=x\cdot mcm(a,b)}$.^[1]​
7. ${\displaystyle mcm(ak,bk)=k\cdot mcm(a,b)}$.
8. Para tres números: ${\displaystyle mcm(a,b,c)=mcm(mcm(a,b),c)}$. Para más valores: ${\displaystyle mcm(a,b\ldots y,z)=mcm(mcm(a,b\ldots y),z)}$

• ${\displaystyle mcm(a,b,c)=abc\iff MCD(a,b,c)=1}$. Esto se debe a las propiedades 5 y 8
• ${\displaystyle mcm(a,b,c)=abc*[a,b,c]/[a,b][b,c][c,a]}$, donde ${\displaystyle [x,y]:=MCD(x,y)}$.^[2]​
• ${\displaystyle mcm\left({\frac {a}{d}},{\frac {b}{d}}\right)=mcm\left({\frac {m}{a}},{\frac {m}{b}}\right)}$, donde ${\displaystyle m:=mcm(a,b),d:=MCD(a,b)}$. Fácil de comprobar con la propiedad 7.
• El mínimo común múltiplo de dos números primos es el total de su multiplicación, conclusión directa de la propiedad 5.
• El Máximo Común Divisor de un grupo de números es un divisor del mínimo común múltiplo de tales números.^[3]​
• Deje que {a, b ... y, z} sea un subconjunto de los números naturales. Entonces, ${\displaystyle mcm(a,b\ldots y,z)\geq mcm(a,b\ldots y)}$, por las propiedades 1 y 8.

La ecuación que une al mínimo común divisor y al Máximo Común Múltiplo es: ${\displaystyle A\cdot B=mcm(A,B)\cdot MCD(A,B)}$. También es descrito como 'si el producto de dos números lo dividimos por su máximo común divisor, dicho cociente es el mínimo común múltiplo'.

Para demostrarlo, deje que X sea el Máximo Común Divisor de A y B, ${\displaystyle X:=MCD(A,B)}$, por lo tanto redefiniremos ${\displaystyle A=PX,B=QX}$. En la página de Máximo común divisor se demostró que si ${\displaystyle \ \operatorname {MCD} (a,b)=d}$ entonces ${\displaystyle \operatorname {MCD} \left({\frac {a}{d}},{\frac {b}{d}}\right)=1}$. Si lo aplicamos a A y B, obtenemos que ${\displaystyle \operatorname {MCD} \left({\frac {A}{d}},{\frac {B}{d}}\right)=\operatorname {MCD} \left({\frac {PX}{X}},{\frac {QX}{X}}\right)=\operatorname {MCD} (P,Q)=1}$

Ahora que P y Q son coprimos, podemos aplicar la quinta propiedad a ellos: ${\displaystyle mcm(PX,QX)=X\cdot mcm(P,Q)=X\cdot PQ}$.

Finalmente, reemplazando: ${\displaystyle A\cdot B=(PX)\cdot (QX)=PQX^{2}}$, y ${\displaystyle mcm(A,B)*MCD(A,B)=(X\cdot PQ)\cdot (X)=PQX^{2}}$, llegando a que ${\displaystyle A\cdot B=mcm(a,b)\cdot MCD(a,b)}$, que era lo que se quería demostrar. ${\displaystyle \Box }$

El mcm se puede emplear para sumar o restar fracciones de distinto denominador, tomando el mcm de los denominadores de las fracciones, y convirtiéndolas en fracciones equivalentes que puedan ser sumadas. Véase el siguiente ejemplo:

${\displaystyle {\frac {1}{6}}+{\frac {4}{33}}}$

Para poder efectuar la suma, primero se debe buscar el mínimo común múltiplo de los denominadores (6 y 33)

luego el mínimo común múltiplo de 6 y 33 es:

${\displaystyle \operatorname {mcm} (6,33)=2\cdot 3\cdot 11=66}$

que corresponde al número 66; ambas fracciones tendrán como denominador 66, ahora solo hay que hallar a cada fracción su fracción equivalente, con denominador 66 y será posible la suma:

${\displaystyle {\cfrac {1}{6}}+{\frac {4}{33}}\quad =\quad {\cfrac {1}{6}}\cdot {\cfrac {\cfrac {66}{6}}{\cfrac {66}{6}}}\;+\;{\cfrac {4}{33}}\cdot {\cfrac {\cfrac {66}{33}}{\cfrac {66}{33}}}\quad =\quad {\cfrac {1\cdot {\cfrac {66}{6}}}{6\cdot {\cfrac {66}{6}}}}\;+\;{\cfrac {4\cdot {\cfrac {66}{33}}}{33\cdot {\cfrac {66}{33}}}}\quad =\quad {\cfrac {1\cdot {\cfrac {66}{6}}}{{\cancel {6}}\cdot {\cfrac {66}{\cancel {6}}}}}\;+\;{\cfrac {4\cdot {\cfrac {66}{33}}}{{\cancel {33}}\cdot {\cfrac {66}{\cancel {33}}}}}\quad =}$

operando las fracciones, podemos realizar la suma:

${\displaystyle {\cfrac {1\cdot 11}{66}}+{\cfrac {4\cdot 2}{66}}\quad =\quad {\cfrac {11}{66}}+{\cfrac {8}{66}}\quad =\quad {\cfrac {19}{66}}}$

El m.c.m. para dos expresiones algebraicas coeficiente numérico y de menor grado que es divisible exactamente por cada una de las expresiones dadas. Esta teoría es de suma importancia para las fracciones y ecuaciones.^[4]​

De esta forma el m.c.m. de monomios ${\displaystyle \ 4a}$ y ${\displaystyle \ 6a^{2}}$ es ${\displaystyle \ 12a^{2}}$ igualmente para ${\displaystyle \ 2x^{2},\ 6x^{3}}$ y ${\displaystyle \ 9x^{4}}$ es ${\displaystyle \ 18x^{4}}$.

Para más de dos números, un algoritmo es el siguiente:

1. Descomponer cada uno de los números en un producto de potencias de factores primos.Por ejemplo, la descomposición factorial de 324 es 2²·3⁴.
2. De entre todos las potencias de factores primos, se eligen todos los existentes, y dentro de los comunes a todos los números, los de mayor potencia. (Es muy conveniente disponer las factorizaciones de manera tabular o matricial para evitar despistes al realizar el ejercicio).
3. Multiplicar todos los factores elegidos.

Por ejemplo, calculando el mcm(324,16,7,5) La descomposición de 324 es 2²·3⁴; la descomposición de 16 es: 2⁴; la descomposición de 7 es 7 y la descomposición de 5 es 5.

${\displaystyle {\begin{bmatrix}324=&2^{2}&3^{4}&&\\16=&2^{4}&&\\5=&&&5&\\7=&&&&7\end{bmatrix}}}$

Por tanto, obtenemos el mcm: 2⁴·3⁴·7·5 = 45360.

El concepto de m.c.m. y de m.c.d. se puede extender a las fracciones o números racionales positivos.^[5]​ Estrictamente hablando cualquier número racional divide a otro racional y no existe un racional mayor o menor que todos. No obstante, la extensión aquí descrita tiene interés en algunos problemas y está relacionada con la teoría de anillos, ideales, identidad de Bézout, teorema de Krull, etc.

En el caso de la aritmética clásica elemental sería de aplicación en el siguiente ejemplo. Sean 3 corredores dando vueltas a un circuito, si en cada vuelta el primero saca 1/3 de vuelta al segundo y 2/7 al tercero. ¿cuándo volverán a coincidir en la meta los tres corredores?. También sería de aplicación en problemas de ruedas dentadas, etc.

Sean dos fracciones ${\displaystyle {\frac {a}{b}}}$ y ${\displaystyle {\frac {c}{d}}}$ irreducibles

${\displaystyle a=\prod _{i}p_{i}^{e_{i}(a)},b=\prod _{i}p_{i}^{e_{i}(b)},c=\prod _{i}p_{i}^{e_{i}(c)},d=\prod _{i}p_{i}^{e_{i}(d)}}$

La descomposición en factores primos de ${\displaystyle a,b,c,d}$. Entonces

${\displaystyle {\frac {\prod _{i}p_{i}^{\max(e_{i}(a),e_{i}(c))}}{\prod _{i}p_{i}^{\min(e_{i}(b),e_{i}(d))}}}}$

es una fracción que es común múltiplo de ${\displaystyle {\frac {a}{b}}}$ y ${\displaystyle {\frac {c}{d}}}$ y es el mínimo por las propiedades del m.c.m. y m.c.d. de dos enteros no negativos ya que ${\displaystyle {\prod _{i}p_{i}^{\max(e_{i}(a),e_{i}(c))}}}$ es el m.c.m. de los numeradores y ${\displaystyle {\prod _{i}p_{i}^{\min(e_{i}(b),e_{i}(d))}}}$ es el m.c.d. de los denominadores de manera que se puede concluir que

${\displaystyle \operatorname {mcm} \left({\frac {a}{b}},{\frac {c}{d}}\right)={\frac {\operatorname {mcm} (a,c)}{\operatorname {mcd} (b,d)}}.}$

Análogamente o teniendo en cuenta que el producto de dos números es igual al de su m.c.m. por su m.c.d. obtenemos:

${\displaystyle \operatorname {mcd} \left({\frac {a}{b}},{\frac {c}{d}}\right)={\frac {\operatorname {mcd} (a,c)}{\operatorname {mcm} (b,d)}}.}$

Las fórmulas anteriores son válidas para una cantidad finita de fracciones. Además el cociente del mcm entre cada fracción es un entero y el conjunto de los cocientes forman un sistema de primos entre sí. De igual manera, el cociente de cada fracción entre el mcd es entero, los cocientes son primos entre sí^[6]​

De manera más general, concepto de m.c.m. tiene sentido en cualquier dominio entero. Mayor uso se da en el conjunto de los enteros, polinomios en una variable, enteros gaussianos^[7]​

• Máximo común divisor
• Número primo
• Mínimo común denominador
• Números naturales

• Mínimo común múltiplo en Enciclopedia libre universal española