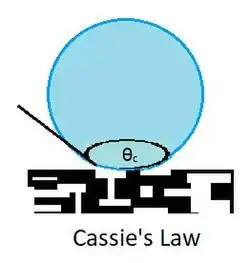
Ley de Cassie

La ley de Cassie, o ecuación de Cassie, describe el ángulo de contacto efectivo θ_c de un líquido sobre una superficie químicamente heterogénea, superficie de un material compuesto formado por diferentes sustancias químicas, es decir, no uniforme en toda su extensión.^[1]​ Los ángulos de contacto son importantes, ya que cuantifican la humectación de una superficie, es decir, la naturaleza de las interacciones intermoleculares entre sólidos y fluidos.^[2]​ La ley de Cassie se reserva para cuando un líquido cubre completamente superficies heterogéneas tanto «lisas» como «rugosas».^[3]​

Más una regla que una ley, la fórmula que se encuentra en la literatura para dos materiales es:

${\displaystyle \cos \theta _{c}=\sigma _{1}\cos \theta _{1}+\sigma _{2}\cos \theta _{2}}$

donde ${\displaystyle \theta _{1}}$ y ${\displaystyle \theta _{2}}$ son los ángulos de contacto para los componentes 1 con área superficial fraccional ${\displaystyle \sigma _{1}}$ y 2 con área superficial fraccional ${\displaystyle \sigma _{2}}$ en el material compuesto, respectivamente. Si existen más de dos materiales, la ecuación se escala a la forma general de:

${\displaystyle \cos \theta _{c}=\sum _{k=1}^{N}\sigma _{k}\cos \theta _{k}}$, con ${\displaystyle \sum _{k=1}^{N}\sigma _{k}=1}$.^[4]​

La ley de Cassie adquiere un significado especial cuando la superficie heterogénea es un medio poroso. ${\displaystyle \sigma _{1}}$ representa ahora el área de la superficie sólida y ${\displaystyle \sigma _{2}}$ los espacios de aire, de modo que la superficie ya no está completamente mojada. El aire crea un ángulo de contacto de ${\displaystyle 180^{\circ }}$ y, como ${\displaystyle \cos(180)}$= ${\displaystyle -1}$, la ecuación se reduce a:

${\displaystyle \cos \theta _{cb}=\sigma _{1}\cos \theta _{1}-\sigma _{2}}$

que es la ecuación de Cassie-Baxter.^[5]​

Desgraciadamente, los términos Cassie y Cassie-Baxter se utilizan a menudo indistintamente, pero no deben confundirse. La ecuación de Cassie-Baxter es más común en la naturaleza y se centra en el «recubrimiento incompleto» de superficies por un líquido únicamente. En el estado de Cassie-Baxter, los líquidos se asientan sobre las asperezas, lo que da lugar a bolsas de aire que quedan atrapadas entre la superficie y el líquido.

La ecuación de Cassie-Baxter no se limita únicamente a superficies «químicamente» heterogéneas, ya que el aire presente en superficies homogéneas porosas hará que el «sistema» sea heterogéneo. Sin embargo, si el líquido penetra en los surcos, la superficie vuelve a ser homogénea y no se puede utilizar ninguna de las ecuaciones anteriores. En este caso, el líquido se encuentra en el estado de Wenzel, regido por una ecuación independiente. Las transiciones entre el estado de Cassie-Baxter y el estado de Wenzel pueden tener lugar cuando se aplican estímulos externos, como presión o vibración, al líquido de la superficie.^[6]​

Cuando una gota de líquido interactúa con una superficie sólida, su comportamiento se rige por la tensión superficial y la energía. La gota de líquido podría extenderse indefinidamente o quedarse sobre la superficie como una cápsula esférica, en cuyo caso existiría un ángulo de contacto.

Definiendo ${\displaystyle E}$ como el cambio de energía libre por unidad de área causado por la extensión de un líquido,

${\displaystyle E=\sigma _{1}(\gamma _{s_{1}a}-\gamma _{s_{1}l})+\sigma _{2}(\gamma _{s_{2}a}-\gamma _{s_{2}l})}$

donde ${\displaystyle \sigma _{1}}$, ${\displaystyle \sigma _{2}}$ son las áreas fraccionarias de los dos materiales en la superficie heterogénea, y ${\displaystyle \gamma _{sa}}$ y ${\displaystyle \gamma _{sl}}$ son las tensiones interfaciales entre el sólido, el aire y el líquido.

El ángulo de contacto para la superficie heterogénea viene dado por: ${\displaystyle \cos \theta _{c}={\frac {E}{\gamma _{la}}}}$, with ${\displaystyle \gamma _{la}}$la tensión interfacial entre el líquido y el aire.

El ángulo de contacto dado por la ecuación de Young es: ${\displaystyle cos\theta _{y}={\frac {\gamma _{sa}-\gamma _{sl}}{\gamma _{la}}}}$

Así, sustituyendo la primera expresión en la ecuación de Young, llegamos a la ley de Cassie para superficies heterogéneas:

${\displaystyle \cos \theta _{c}=\sigma _{1}\cos \theta _{1}+\sigma _{2}\cos \theta _{2}}$^[1]​

Los estudios sobre el ángulo de contacto existente entre un líquido y una superficie sólida comenzaron con Thomas Young en 1805.^[7]​ La ecuación de Young

${\displaystyle cos\theta _{y}={\frac {\gamma _{sa}-\gamma _{sl}}{\gamma _{la}}}}$

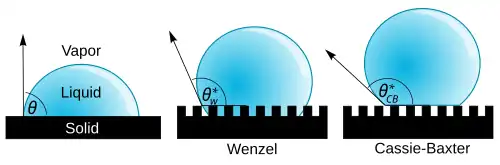
refleja la fuerza relativa de la interacción entre las tensiones superficiales en el contacto de las tres fases, y es la relación geométrica entre la energía obtenida al formar una unidad de área de la interfaz sólido-líquido y la necesaria para formar una interfaz líquido-aire.^[1]​ Sin embargo, la ecuación de Young solo funciona para superficies «ideales» y «reales», y en la práctica la mayoría de las superficies son microscópicamente rugosas.

En 1936, Robert Wenzel modificó la ecuación de Young para tener en cuenta las superficies homogéneas rugosas, y se introdujo un parámetro ${\displaystyle r}$, definido como la relación entre el área real del sólido y su área nominal.^[8]​ Conocida como la ecuación de Wenzel,

${\displaystyle \cos \theta _{w}=r\cos \theta _{y}}$

muestra que el «ángulo de contacto aparente», el ángulo medido en una inspección casual, aumentará si la superficie se vuelve rugosa. Se sabe que los líquidos con un ángulo de contacto ${\displaystyle \theta _{w}}$ se encuentran en el estado de Wenzel.