Lógica categórica

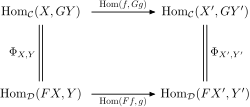
La lógica categórica es una rama de las matemáticas, particularmente de la lógica matemática, que investiga a los sistemas formales usando conceptos de teoría de categorías; particularmente, el uso de nociones como categoría cartesiana cerrada o topos. También es notable por sus conexiones con la informática teórica, teoría de tipos, y la teoría de tipos homotópica.^[1]​ En términos generales, la lógica categórica representa tanto la sintaxis como la semántica de sistemas formales mediante una categoría, y una interpretación mediante un funtor. Las conectiva lógicas y los cuantificadores pueden interpretarse, de igual forma, como funtores adjuntos sobre una categoría cartesiana cerrada. El marco categórico proporciona un rico marco conceptual para construcciones lógicas y de teoría de tipos. Su estudio inició a finales de 1960 siguiendo el trabajo pionero de William Lawvere.

Algunos de los temas principales abordados mediante el enfoque categórico son los siguientes:

Semántica categórica

La lógica categórica introduce la noción de estructura valuada en una categoría C con la noción modelo-teorética clásica de una estructura que aparece en el caso particular donde C es la categoría de conjuntos y funciones. Esta noción ha demostrado ser útil cuando la noción de teoría de conjuntos de un modelo carece de generalidad y/o resulta inconveniente. El modelado de RAG Seely de varias teorías impredicativas, como el Sistema F, es un ejemplo de la utilidad de la semántica categórica.

Según el trabajo de William Lawvere sobre hiperdoctrinas,^[2]​ los conectores y cuantificadores de la lógica de primer orden se podían representar bajo el concepto de functores adjuntos. Por ejemplo, la adjunción entre el cuantificador universal y el cuantificador existencial surge naturalmente bajo las reglas de eliminación e introducción de estos mismos cuantificadores en deducción natural.^[3]​^[4]​

Lenguajes internos

Esto puede verse como una formalización y generalización de la prueba mediante la búsqueda de diagramas . Se define un lenguaje interno adecuado que nombra los constituyentes relevantes de una categoría y luego se aplica la semántica categórica para convertir las afirmaciones en una lógica sobre el lenguaje interno en declaraciones categóricas correspondientes. Esto ha tenido mucho éxito en la teoría de topos, donde el lenguaje interno de un topos junto con la semántica de la lógica intuicionista de orden superior en un topos permite razonar sobre los objetos y morfismos de un topos como si fueran conjuntos y funciones. ^[5]​ Esto ha tenido éxito al tratar con topos que tienen "conjuntos" con propiedades incompatibles con la lógica clásica. Un buen ejemplo es el modelo de cálculo lambda no tipificado de Dana Scott en términos de objetos que se retraen en su propio espacio funcional . Otro es el modelo Moggi -Hyland del sistema F mediante una subcategoría interna completa del topos efectivo de Martin Hyland .

Construcciones de modelos de términos

En muchos casos, la semántica categórica de una lógica proporciona una base para establecer una correspondencia entre teorías en la lógica e instancias de un tipo apropiado de categoría. Un ejemplo clásico es la correspondencia entre las teorías de la lógica ecuacional βη sobre el cálculo lambda simplemente tipificado y las categorías cerradas cartesianas, conocida como correspondencia de Curry-Howard-Lambek (que incluye la correspondencia entre tipos y proposiciones lógicas). Las categorías que surgen de las teorías a través de construcciones de modelos de términos generalmente se pueden caracterizar hasta su equivalencia mediante una propiedad universal adecuada. Esto ha permitido realizar pruebas de propiedades metateóricas de algunas lógicas por medio de un álgebra categórica apropiada. Por ejemplo, Freyd dio una prueba de las propiedades de disyunción y existencia de la lógica intuicionista de esta manera.

Recuérdese que una categoría puede ser entendida como un conjunto parcialmente ordenado (donde cada morfismo ${\displaystyle A\rightarrow B}$ puede ser visto como ${\displaystyle A\leq B}$), de tal modo que si una categoría contiene todos los límites y colímites, puede ser interpretada como un retículo. Más específicamente, si esta categoría es cartesiana cerrada y tiene un objeto inicial y terminal, la categoría puede ser entendida como un álgebra de Heyting o un álgebra de Boole dependiendo el caso.

Sea el objeto terminal interpretado como 1 o verdadero y el objeto inicial entendido como 0 o falso, y sea ${\displaystyle {\mathcal {H}}}$ nuestra álgebra de Heyting (que es una categoría); tendremos entonces los siguientes funtores y adjunciones:

${\displaystyle \land :{\mathcal {H}}\times {\mathcal {H}}\rightarrow {\mathcal {H}}}$, tal que: ${\displaystyle (\phi ,\psi )\mapsto \phi \land \psi }$. Y tendremos la adjunción ${\displaystyle \Delta \dashv \land }$, donde ${\displaystyle \Delta }$ es el funtor diagonal ${\displaystyle \Delta :{\mathcal {H}}\rightarrow {\mathcal {H}}\times {\mathcal {H}}}$ definido por ${\displaystyle \Delta (a)=\langle a,a\rangle }$.

${\displaystyle \lor :{\mathcal {H}}\times {\mathcal {H}}\rightarrow {\mathcal {H}}}$, tal que: ${\displaystyle (\phi ,\psi )\mapsto \phi \lor \psi }$. Y tendremos la adjunción ${\displaystyle \lor \dashv \Delta }$.

${\displaystyle \Rightarrow :{\mathcal {H}}\times {\mathcal {H}}\rightarrow {\mathcal {H}}}$, tal que: ${\displaystyle (\phi ,\psi )\mapsto \phi \Rightarrow \psi }$. Y tendremos la adjunción ${\displaystyle (-\land A)\dashv (-)^{A}}$, siendo A cualquier objeto de la categoría.

${\displaystyle \neg :{\mathcal {H}}\rightarrow {\mathcal {H}}^{op}}$, tal que: ${\displaystyle \phi \mapsto \neg \phi ;\phi \rightarrow \psi \mapsto \neg \psi \rightarrow \neg \phi }$, donde ${\displaystyle {\mathcal {H}}^{op}}$ es su categoría opuesta.

Cuando trabajamos en un álgebra bi-Heyting (es decir, que opera tanto con la negación de Heyting y negación de co-Heyting, podemos definir los operadores modales ${\displaystyle \Box ,\Diamond }$ con ambas negaciones, dándonos otra situación de funtores adjuntos.

Formalmente, sea ${\displaystyle \neg }$ la negación de Heyting y sea ${\displaystyle \sim }$ la negación de co-Heyting. Entonces definimos: ${\displaystyle \Diamond =\sim \neg }$ y ${\displaystyle \Box =\neg \sim }$, la composición de ambas como funtores (donde la negación de co-Heyting se define análogamente a su contraparte). Además tendremos la siguiente adjunción ${\displaystyle \Diamond \dashv \Box }$.^[6]​

Esta exposición sigue el trabajo original de Lawvere.

Primero definiremos una categoría cartesiana cerrada ${\displaystyle \mathbf {T} }$ cuyos objetos serán tipos o contextos, los morfismos se interpretan como términos y el morfismo ${\displaystyle 1\rightarrow C}$ del objeto terminal a cualquier otro objeto una constante de tipo ${\displaystyle C}$.

Entonces, una hiperdoctrina se define como un funtor ${\displaystyle P:\mathbf {T} ^{op}\rightarrow \mathbb {C} }$ sobre un lenguaje ${\displaystyle {\mathcal {L}}}$ (que puede ser de cualquier lógica), y donde ${\displaystyle \mathbb {C} }$ es una 2-categoría (o de mayor orden), tal que sus objetos tengan una lógica interna correspondiente a ${\displaystyle {\mathcal {L}}}$. Por ejemplo, podemos dejar que ${\displaystyle \mathbb {C} }$ sea una categoría de conjuntos parcialmente ordenados, o de retículos o de álgebras de Heyting. Para toda ${\displaystyle X\in \mathbf {T} ,P(X)}$ se llamará la categoría de atributos o de predicados sobre ${\displaystyle X}$.

Otro ejemplo canónico es aquel en que la hiperdoctrina envía a cada ${\displaystyle X}$ a su retículo, o álgebra, de subobjetos (que puede entenderse como el clásico retículo formado por los subconjuntos de un conjunto ordenados bajo inclusión). En este sentido, también se dice que una hiperdoctrina asigna a cada objeto una categoría similar a una sobrecategoría (un caso especial de la categoría coma), o una axiomatización de sus sobrecategorías.^[7]​

La acción de la hiperdoctrina, al ser un funtor contravariante, es tal que, a cada morfismo ${\displaystyle f:X\rightarrow Y}$ en ${\displaystyle \mathbf {T} }$, asigna la operación de sustitución de variables para los predicados, o proposiciones, de cada contexto; es decir ${\displaystyle P(f):P(Y)\rightarrow P(X)}$. Ahora veremos cómo los cuantificadores son adjuntos a ${\displaystyle P(f)}$.

En tanto ${\displaystyle \mathbf {T} }$ es cartesiana cerrada, existe el producto de cada colección de objetos. Pensemos en ${\displaystyle X\times Y}$ y sus proyecciones respectivas ${\displaystyle \pi _{X},\pi _{Y}}$. Entonces por contravarianza tendremos ${\displaystyle P(\pi _{X}):P(X)\rightarrow P(X\times Y)}$, que puede verse como agregar una variable ${\displaystyle Y}$ libre (o varias) al contexto de ${\displaystyle X}$. En tanto el codominio de la hiperdoctrina es una 2-categoría, tendremos que ${\displaystyle P(\pi _{X})}$ es un funtor, por lo que podemos definir dos funtores adjuntos que reviertan lo que hace ${\displaystyle P(\pi _{X})}$; es decir, que eliminen las variables libres agregada al contexto ${\displaystyle X}$. Como puede verse, estos corresponderán, entonces, a cuantificar sobre ${\displaystyle Y}$.

Definiremos dos funtores ${\displaystyle \forall _{Y}:P(X\times Y)\rightarrow P(X),\exists _{Y}:P(X\times Y)\rightarrow P(X)}$, que tendrán la siguiente adjunción: ${\displaystyle \exists _{Y}\dashv P(\pi _{X})\dashv \forall _{Y}}$. Esto implica la siguiente situación (donde ${\displaystyle A\vdash B}$ significa ${\displaystyle A\rightarrow B}$, ${\displaystyle \star =P(\pi _{X})}$ por brevedad y ${\displaystyle \phi ,\psi }$ son elementos de la 2-categoría, es decir, predicados):

${\displaystyle {\begin{array}{c}\star (\phi ({\bar {x}}))\vdash \psi ({\bar {x}},y)\\\hline \phi ({\bar {x}})\vdash \forall _{y}\psi ({\bar {x}},y)\end{array}}{\begin{array}{c}\exists _{y}\psi ({\bar {x}},y)\vdash \phi ({\bar {x}})\\\hline \psi ({\bar {x}},y)\vdash \star (\phi ({\bar {x}}))\end{array}}}$

Así, es fácil ver que la counidad de la adjunción ${\displaystyle P(\pi _{X})\dashv \forall _{Y}}$ es simplemente la regla de eliminación de ${\displaystyle \forall }$ y la unidad de la adjunción ${\displaystyle \exists _{Y}\dashv P(\pi _{X})}$ la regla de introducción de ${\displaystyle \exists }$ en deducción natural.^[4]​^[8]​

• Historia de la teoría de topos
• Teoría de categorías
• William Lawvere

1. ↑ Goguen, Joseph; Mossakowski, Till; de Paiva, Valeria; Rabe, Florian; Schroder, Lutz (2007). «An Institutional View on Categorical Logic». International Journal of Software and Informatics 1 (1): 129-152. 
2. ↑ Lawvere, F. William (1969). «Adjointness in Foundations». Dialectica 23 (3/4): 281-296. ISSN 0012-2017. Consultado el 4 de mayo de 2025. 
3. ↑ Lawvere, 1971, Quantifiers and Sheaves
4. ↑ ^{a b} Awodey, Steve (2006). Category Theory. Oxford University Press. Consultado el 4 de mayo de 2025. 
5. ↑ Aluffi, 2009
6. ↑ Rosiak, Daniel (25 de octubre de 2022). Sheaf Theory through Examples (en inglés). The MIT Press. ISBN 978-0-262-37042-4. Consultado el 5 de mayo de 2025. 
7. ↑ «hyperdoctrine in nLab». ncatlab.org. Consultado el 5 de mayo de 2025. 
8. ↑ «Introduction to Higher-Order Categorical Logic». Cambridge University Press & Assessment (en inglés). Consultado el 5 de mayo de 2025. 

• Chang, Chen Chung; Keisler, H. Jerome (1990), Model Theory, Studies in Logic and the Foundations of Mathematics, Elsevier, ISBN 978-0-444-88054-3 .
• Corcoran, John (1980), «Categoricity», History and Philosophy of Logic 1 (1–2): 187-207, doi:10.1080/01445348008837010 .
• Hodges, Wilfrid, "First-order Model Theory", The Stanford Encyclopedia of Philosophy (Summer 2005 Edition), Edward N. Zalta (ed.).
• Marker, David (2002), Model theory: An introduction, Graduate Texts in Mathematics 217, New York, NY: Springer-Verlag, ISBN 0-387-98760-6, Zbl 1003.03034 .
• Monk, J. Donald (1976), Mathematical Logic, Springer-Verlag, ISBN 978-1-4684-9454-9, doi:10.1007/978-1-4684-9452-5 .
• Morley, Michael (1965), «Categoricity in Power», Transactions of the American Mathematical Society (American Mathematical Society, Vol. 114, No. 2) 114 (2): 514-538, ISSN 0002-9947, JSTOR 1994188, doi:10.2307/1994188 .
• Palyutin, E.A. (2001), «Lógica categórica», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Shelah, Saharon (1974), «Categoricity of uncountable theories», Proceedings of the Tarski Symposium (Proc. Sympos. Pure Math., Vol. XXV, Univ. of California, Berkeley, Calif., 1971), Proceedings of Symposia in Pure Mathematics 25, Providence, R.I.: American Mathematical Society, pp. 187-203, ISBN 9780821814253, MR 0373874, doi:10.1090/pspum/025/0373874 .
• Shelah, Saharon (1990), Classification theory and the number of nonisomorphic models, Studies in Logic and the Foundations of Mathematics (2nd edición), Elsevier, ISBN 978-0-444-70260-9, (requiere registro) . (IX, 1.19, pg.49)
• Veblen, Oswald (1904), «A System of Axioms for Geometry», Transactions of the American Mathematical Society (American Mathematical Society, Vol. 5, No. 3) 5 (3): 343-384, ISSN 0002-9947, JSTOR 1986462, doi:10.2307/1986462 .