Intersección de conjuntos

¿Qué cosas tienen en común tus dos materias favoritas?

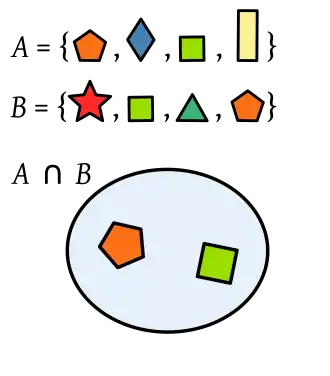
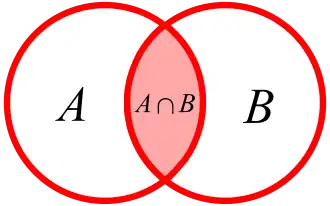
La intersección de $A$ y $B$ es otro conjunto $A \cap B$ que contiene sólo los elementos que pertenecen tanto a $A$ como a $B$ .

En teoría de conjuntos, la intersección de dos conjuntos A y B es el conjunto de elementos que están tanto en A como en B y se representa como A ∩ B, donde el símbolo "∩" indica los elementos que pretenecen simultáneamente a ambos conjuntos.

Por ejemplo,dado el conjunto de los números pares $P$ y el conjunto de los cuadrados $C$ de números naturales, su intersección es el conjunto de los cuadrados pares.

P=\{2,4,6,8,10,\ldots \}

C=\{1,4,9,16,25,\ldots \}

D=\{4,16,36,64,\ldots \}

, $D = P \cap C$ .

En otras palabras: por ejemplo, si A = { a, b, c, d, e, f} y B = { a, e, i, o, u}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A $\cap$ B = { a, e}

Ejemplos didácticos:

A = {manzana, pátano, uva} B = {uva, piña, pera} Intersección: A ∩ B = {uva}
Si A={ Luis, Ana, Martha} son estudiantes de matemáticas y B = { Martha, Karla, Luis}, entonces: A $\cap$ B = { Luis, Martha}
Conjunto A {azul} Conjunto B {rojo} Intersección {morado}

Definición

La intersección de dos superficies oblicuas.
La intersección de dos superficies perpendiculares.
La intersección de dos superficies perpendiculares.
Intersección de 3 conjuntos (diagrama de Venn).
Intersección de dos conjuntos $A$ y $B$ .

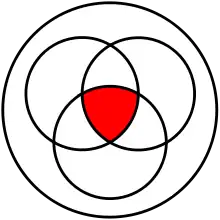
La intersección de conjuntos es cuando comparamos dos conjuntos y buscamos los elementos que tienen en común.

Por ejemplo, si un conjunto A tiene {1,2,3} y su conjunto b tiene {2,3,4}, entonces su intersección es {2,3}, porque esos son los que aparecen en ambos conjuntos.

En matemáticas, usamo el símbolo "∩" para representar la intersección. Así que escribimos: A∩B= {2,3}

Dados dos conjuntos $A$ y $B$ , su intersección es otro subconjunto cuyos elementos, necesariamente, pertenecen a ambos conjunto.

Intersección con símbolos y número

$A = {π, c, 8, γ, 5, P}$ y $B = {ω, c, 0, Δ, 5, R}$ .

Entonces la intersección es $A \cap B = {5, c}$ .

Intersección naturales

C = {números naturales que son potencias de 2} → {2, 4, 8, 16, 32, 64, 128, ..

D = {números que son cubos perfectos} → {1, 8, 27, 64, 125, 216, 512, ...}

Entonces la intersección es C ∩ D = {8, 64, 512, ...}

Intersección de pares e impares

Sean los conjuntos de números pares e impares. Su intersección es el conjunto vacío ∅, ya que no existe ningún número natural que sea par e impar a la vez.

Cuando la intersección de dos conjuntos es vacía, se dice que son disjuntos:

Dos conjuntos $A$ y $B$ se dicen disjuntos si su intersección es el conjunto vacío:

$A\cap B=\varnothing$

Generalizaciones

La intersección de un número finito de conjuntos, superior a dos, se define teniendo en cuenta que, debido a la propiedad asociativa (más abajo), el orden en el que se intersequen los conjuntos es irrelevante:

$A_{1}\cap A_{2}\cap \ldots \cap A_{n}=A_{1}\cap (A_{2}\cap (\ldots (A_{n-1}\cap A_{n}){\scriptstyle \ldots })$

La definición más general en teoría de conjuntos se refiere a una familia de conjuntos, un conjunto cuyos elementos son conjuntos a su vez:

Sea $M$ una familia de conjuntos. Su intersección $\cap M$ se define como:

$x\in \bigcap M{\text{ si para cada }}A\in M{\text{ se tiene que }}x\in A$

De este modo, la intersección de un número finito de conjuntos es sólo un caso particular de esta definición general:

A \cap B = \cap M

, donde

M = {A, B}

A 1 \cap ... \cap A n = \cap M

, donde

M = {A 1, ..., A n}

La intersección general de conjuntos se denota de diversas maneras:

$\bigcap M=\bigcap _{A\in M}A=\bigcap _{i\in I}A_{i}{\text{ ,}}$

donde esta última se aplica en el caso de que utilicemos un conjunto índice, definiendo $M$ como ${A i : i \in I}$ .

Propiedades

De la definición de intersección puede deducirse directamente:

Idempotencia. La intersección de un conjunto $A$ consigo mismo es el propio $A$ :

$A\cap A=A$

La intersección de $A$ y $B$ es un subconjunto de ambos:

$A\cap B\subseteq A,B$

La intersección de un conjunto $B$ con un conjunto $A$ que lo contenga, deja a $B$ inalterado:

$B\subseteq A\rightarrow A\cap B=B$

La intersección de conjuntos poseen también propiedades similares a las operaciones con números:

Propiedad asociativa. La intersección de los conjuntos $A$ y $B \cap C$ es igual a la intersección de los conjuntos $A \cap B y C$ :

$(A\cap B)\cap C=A\cap (B\cap C)$

Propiedad conmutativa. La intersección de los conjuntos $A$ y $B$ es igual a la intersección de los conjuntos $B$ y $A$ :

$A\cap B=B\cap A$

Elemento absorbente. La intersección de un conjunto $A$ con el conjunto vacío $\emptyset$ es $\emptyset$ :

$A\cap \varnothing =\varnothing$

Todas estas propiedades se deducen de propiedades análogas para la conjunción lógica.

En relación con la operación de unión existen unas leyes distributivas:

Propiedad distributiva

$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ , y por tanto:
$A \cup (A \cap B) = A$

$A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ , y por tanto:
$A \cap (A \cup B) = A$

Se cumple que ∅ ⊂ A∩B∩C ⊂ A∩B ⊂ A ⊂ A∪B ⊂ A∪B∪C ⊂ Ω donde Ω es el conjunto universal.^[1]

Teoría axiomática

En las teorías axiomáticas de conjuntos usuales, como ZFC o NBG, la existencia de la intersección de una familia de conjuntos no se postula de manera independiente, sino que se demuestra como consecuencia del esquema axiomático de reemplazo.

Véase también

Referencias

↑ Rojo. Álgebra I

Literatura del tema

Dorronsoro, José; Hernández, Eugenio (1996). Números, grupos y anillos. Addison-Wesley/Universidad Autónoma de Madrid. ISBN 84-7829-009-5.
Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.

Yu. M. Korshunov. Fundamentos matemáticos de la cibernética. Editorial Mir, Moscú s/f.

Datos: Q185837
Multimedia: Intersection (set theory) / Q185837

[1] Rojo. Álgebra I

[1]