Gusanos de Paterson

Los gusanos de Paterson son una familia de autómatas celulares ideados en 1971 por Mike Paterson y John Horton Conway para modelizar el comportamiento y las pautas de alimentación de ciertos gusanos prehistóricos. En el modelo, un gusano se desplaza entre puntos de una rejilla triangular a lo largo de segmentos de línea, que representan el alimento. Sus giros vienen determinados por la configuración de los segmentos de línea comidos y no comidos adyacentes al punto en el que se encuentra el gusano en ese momento. A pesar de regirse por reglas sencillas, el comportamiento de los gusanos puede ser extremadamente complejo, y aún se desconoce el destino final de una variante.

Los gusanos fueron estudiados a principios de la década de 1970 por Paterson, Conway y Michael Beeler, descritos por Beeler en junio de 1973,^[1]​ y presentados en noviembre de 1973 en la columna «Mathematical Games» de Martin Gardner en Scientific American.^[2]​

El juego Worms? de Electronic Arts de 1983 es una implementación interactiva de los gusanos de Paterson, en la que cada vez que un gusano tiene que girar en un sentido para el que carece de regla, se detiene y deja que el usuario elija una dirección, que establece esa regla para ese gusano.

Los gusanos de Paterson intentan simular el comportamiento de los gusanos prehistóricos. Estas criaturas se alimentaban de los sedimentos del fondo de los estanques y evitaban desandar caminos ya recorridos porque allí el alimento escaseaba pero, como la comida se encontraba en parches, a los gusanos les interesaba permanecer cerca de los senderos anteriores. Las distintas especies de gusanos tenían reglas innatas diferentes en cuanto a la proximidad a los caminos recorridos, el momento de girar y la brusquedad del giro.^[1]​ En 1969, Raup y Seilacher crearon simulaciones por computadora de las rutas fosilizadas de los gusanos, y estas simulaciones inspiraron a Paterson y Conway para desarrollar un conjunto sencillo de reglas para estudiar gusanos idealizados en cuadrículas regulares.^[3]​

El modelo original de Conway era un gusano sobre una rejilla ortogonal, pero sólo produjo tres especies diferentes de gusanos, todos ellos con un comportamiento poco interesante. Paterson consideró gusanos en una rejilla triangular.^[1]​ Los gusanos de Paterson fueron descritos por Beeler en un memorándum sobre IA del Instituto Tecnológico de Massachusetts (#[1]) y presentados en noviembre de 1973 en la columna «Mathematical Games» de Martin Gardner en Scientific American,^[2]​ y posteriormente reimpresos en Gardner 1986.^[4]​ Estas simulaciones diferían en su planteamiento de otros autómatas celulares desarrollados por la misma época, que se centraban en las células y las relaciones entre ellas.^[5]​ Los modelos informáticos sencillos como éstos son demasiado abstractos para describir con exactitud el comportamiento de las criaturas reales, pero demuestran que incluso reglas muy simples pueden dar lugar a patrones parecidos a sus huellas.^[6]​

El gusano comienza en algún punto de una cuadrícula triangular infinita. Comienza a moverse a lo largo de una de las seis cuadrículas que se encuentran en cada punto^[6]​ y, una vez que ha recorrido una unidad de distancia, llega a un nuevo punto. A continuación, el gusano decide, en función de la distribución de las cuadrículas recorridas y no recorridas, qué dirección va a tomar. Las direcciones son relativas al punto de vista del gusano. Si el gusano no se ha encontrado antes con esta distribución exacta, puede salir por cualquier cuadrícula no recorrida. A partir de ese momento, si vuelve a encontrarse con esa distribución, deberá moverse de la misma manera. Si no hay ninguna cuadrícula disponible, el gusano muere y la simulación termina.^[1]​

Existen muchos tipos diferentes de gusanos en función de la dirección en la que giran al encontrarse con un nuevo tipo de intersección. Las distintas variedades de gusano pueden clasificarse sistemáticamente asignando a cada dirección un número y enumerando la elección realizada cada vez que se encuentra un nuevo tipo de intersección.^[7]​

Las seis direcciones están numeradas del siguiente modo:

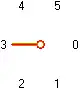
Así, la dirección 0 indica que el gusano sigue avanzando en línea recta, la dirección 1 indica que el gusano hará un giro a la derecha de 60° y lo mismo para las demás direcciones. El gusano no puede viajar en la dirección 3 porque esa es la cuadrícula que acaba de atravesar. Así, un gusano con la regla {1,0,5,1} decide viajar en la dirección 1 la primera vez que tiene que hacer una elección, en la dirección 0 la siguiente vez que tiene que hacer una elección y así sucesivamente. Si sólo hay una línea de cuadrícula disponible, el gusano no tiene más remedio que tomarla y normalmente no se indica explícitamente.

Un gusano cuyo conjunto de reglas empieza por 0 continúa en línea recta para siempre. Este es un caso trivial, por lo que normalmente se estipula que el gusano debe girar cuando encuentre un punto con sólo líneas de cuadrícula sin comer. Además, para evitar duplicados simétricos en espejo, el primer giro del gusano debe ser a la derecha.^[1]​ Un gusano muere si vuelve a su origen por tercera vez, porque entonces no hay aristas no recorridas disponibles. Sólo el origen puede ser letal para el gusano.^[8]​

Existen 1.296 combinaciones posibles de reglas de gusano,^[4]​ lo que puede comprobarse mediante el siguiente argumento:

1. Si el gusano encuentra un nodo sin segmentos comidos, aparte del que acaba de comer, puede dar un giro brusco o uno suave. Esta es la situación que se muestra en la figura anterior. Dado que la elección inicial de izquierda o derecha produce combinaciones que son simples espejos una de otra, no son efectivamente diferentes.
2. Si encuentra un nodo con un segmento comido, puede salir por cualquiera de los cuatro restantes. Sólo la primera vuelta del gusano al origen tiene este carácter.
3. En el caso de dos segmentos comidos, la ubicación de éstos es importante. El único tipo de intersecciones de dos segmentos que puede existir es el producido por la primera regla, para la que existen cuatro direcciones de aproximación distintas, cada una de las cuales ofrece la posibilidad de elegir entre tres direcciones de salida. Esto permite 81 alternativas diferentes a la hora de elegir las reglas
4. Si el gusano vuelve al origen, se encontrará con tres segmentos comidos y deberá elegir entre los dos restantes sin comer, independientemente de su distribución.
5. Para cuatro segmentos comidos, sólo queda un segmento sin comer y el gusano debe tomarlo.

Hay, por tanto, 2×4×81×2x1=1.296 combinaciones diferentes de reglas. Muchas de ellas son duplicados especulares de otras, y otras mueren antes de tener que hacer todas las elecciones de su conjunto de reglas, lo que deja 411 especies distintas (412 si se incluye el gusano de línea recta infinita).^[8]​ 336 de estas especies acaban muriendo. 73 patrones muestran un comportamiento infinito, es decir, se asientan en un patrón repetitivo que no vuelve al origen. Se cree firmemente que otros dos son infinitos y uno sigue sin resolverse. Once de las normas muestran un comportamiento complicado. No mueren ni siquiera después de muchos miles de millones de iteraciones, ni adoptan un patrón obviamente infinito. Su destino final era desconocido hasta 2003, cuando Benjamin Chaffin desarrolló nuevos métodos para resolverlas. Tras muchas horas de ordenador, se resolvieron nueve de las once reglas, dejando a los gusanos con las reglas {1,0,4,2,0,2,0} y {1,0,4,2,0,1,5}.^[7]​ La primera de ellas fue resuelta por Tomas Rokicki, que determinó que se detiene tras 57 billones (5,7×10¹³) de pasos de tiempo, dejando sólo {1,0,4,2,0,1,5} sin resolver. Según Rokicki, el gusano sigue activo después de 5,2×10¹⁹ pasos de tiempo. Utilizó un algoritmo basado en el Hashlife de Bill Gosper para simular los gusanos a velocidades extraordinarias.^[8]​ Este comportamiento es considerablemente más complejo que el del gusano de rejilla rectangular relacionado, que tiene un camino más largo de sólo 16 segmentos.^[6]​

Es posible que dos especies diferentes de gusanos produzcan el mismo camino, aunque no necesariamente lo recorran en el mismo orden.^[1]​ El camino más común es también el más corto: el símbolo de la prueba MOT/refugio de siete puntos.^[4]​ Un ejemplo de este camino se muestra en la figura animada de arriba. En total hay 299 trayectorias diferentes, y 209 de ellas son producidas por una sola especie.^[1]​

• Hormiga de Langton - Máquina de Turing bidimensional con comportamiento emergente
• Máquina de Turing - Modelo de computación que define una máquina abstracta
• Turmite - Máquina de Turing en una cuadrícula bidimensional

• Página del gusano de Rokicki
• Página del gusano de Sven