Grafo Halin

Un grafo Halin

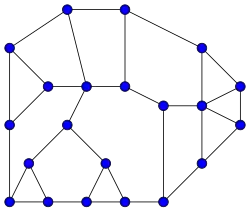
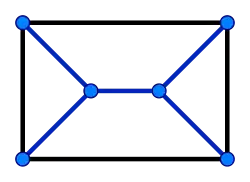
En teoría de grafos, un grafo Halin es un tipo de grafo plano que se construye conectando las hojas de un árbol en un ciclo. El árbol debe tener al menos cuatro vértices, ninguno de los cuales tiene exactamente dos vecinos; debe dibujarse en el plano de modo que ninguna de sus aristas se cruce (esto se denomina incrustación plana), y el ciclo conecta las hojas en el orden de las agujas del reloj en esta incrustación. Así, el ciclo forma la cara exterior del grafo de Halin, con el árbol en su interior.[1]​

Los grafos de Halin deben su nombre al matemático alemán Rudolf Halin, que los estudió en 1971.[2]​ Los grafos de Halin cúbicos -aquellos en los que cada vértice toca exactamente tres aristas- ya habían sido estudiados más de un siglo antes por Kirkman.[3]​ Los grafos de Halin son grafos poliédricos, lo que significa que cada grafo de Halin puede utilizarse para formar los vértices y aristas de un poliedro convexo, y los poliedros formados a partir de ellos se han denominado poliedros sin techo o cúpulas.

Todo grafo de Halin tiene un ciclo hamiltoniano a través de todos sus vértices, así como ciclos de casi todas las longitudes hasta el número de vértices del grafo. Los grafos de Halin pueden reconocerse en tiempo lineal. Dado que los grafos de Halin tienen poca anchura de árbol, muchos problemas computacionales que son difíciles de resolver en otros tipos de grafos planos, como la búsqueda de ciclos de Hamilton, pueden resolverse rápidamente en grafos de Halin.

Ejemplos

Una estrella es un árbol con exactamente un vértice interno. Aplicando la construcción del grafo de Halin a una estrella se obtiene un grafo de rueda, el grafo de las (aristas de) una pirámide.[4]​ El grafo de un prisma triangular es también un grafo de Halin: se puede dibujar

La gráfica de un prisma triangular
Un prisma triangular, construido como un grafo de Halin a partir de un árbol de seis vértices
Grafos de rueda con cuatro a nueve vértices
Grafo de rueda

de forma que una de sus caras rectangulares sea el ciclo exterior, y las aristas restantes formen un árbol con cuatro hojas, dos vértices interiores y cinco aristas.[5]​

El grafo de Frucht, uno de los cinco grafos cúbicos más pequeños sin automorfismos gráficos no triviales,[6]​ también es un grafo de Halin.[7]​

Propiedades

Todo grafo de Halin está conectado por 3, lo que significa que no es posible eliminar dos vértices de él y desconectar los vértices restantes. Es de 3 aristas mínimas, lo que significa que si se elimina alguna de sus aristas, el grafo restante deja de ser de 3 aristas.[1]​Por el teorema de Steinitz, como grafo plano de 3 aristas, se puede representar como el conjunto de vértices y aristas de un poliedro convexo; es decir, es un grafo poliédrico. El poliedro que realiza el grafo puede elegirse de modo que la cara que contiene todas las hojas del árbol sea horizontal y todas las demás caras queden por encima de ella, con pendientes iguales.[8]​ Como todo grafo poliédrico, los grafos de Halin tienen una única incrustación plana, hasta la elección de cuál de sus caras será la cara exterior.[1]​

Todo grafo de Halin es un grafo hamiltoniano, y cada arista del grafo pertenece a un ciclo hamiltoniano. Además, todo grafo de Halin sigue siendo hamiltoniano tras la eliminación de cualquier vértice.[9]​ Dado que todo árbol sin vértices de grado 2 contiene dos hojas que comparten el mismo padre, todo grafo de Halin contiene un triángulo. En particular, no es posible que un grafo de Halin sea un grafo sin triángulos ni un grafo bipartito.[10]​

Además, todo grafo de Halin es casi pancíclico, en el sentido de que tiene ciclos de todas las longitudes de 3 a n, con la posible excepción de una única longitud par. Además, todo grafo de Halin sigue siendo casi pancíclico si se contrae una sola arista, y todo grafo de Halin sin vértices interiores de grado tres es pancíclico.[11]​

El número cromático de incidencia de un grafo Halin G con grado máximo Δ(G) mayor que cuatro es Δ(G) + 1.[12]​ Este es el número de colores necesarios para colorear todos los pares (v,e) donde v es un vértice del grafo, y e es una arista incidente a v, obedeciendo ciertas restricciones en la coloración. Los pares que comparten un vértice o una arista no pueden tener el mismo color. Además, un par (v,e) no puede tener el mismo color que otro par que utilice el otro extremo de e. Para grafos Halin con Δ(G) = 3 o 4, el número cromático de incidencia puede llegar a 5 o 6, respectivamente.[13]​

Complejidad computacional

Es posible comprobar si un grafo de n vértices es un grafo de Halin en tiempo lineal, encontrando una incrustación plana del grafo (si existe) y comprobando si existe una cara que tenga al menos n/2 + 1 vértices, todos de grado tres. En caso afirmativo, puede haber como máximo cuatro de estas caras, y es posible comprobar en tiempo lineal para cada una de ellas si el resto del grafo forma un árbol con los vértices de esta cara como hojas.[14]​ Alternativamente, un grafo con n vértices y m aristas es Halin si y sólo si es plano, está conectado por 3 y tiene una cara cuyo número de vértices es igual al rango del circuito m - n + 1 del grafo, todo lo cual puede comprobarse en tiempo lineal.[15]​ Otros métodos para reconocer grafos Halin en tiempo lineal incluyen la aplicación del teorema de Courcelle, o un método basado en la reescritura de grafos, ninguno de los cuales se basa en conocer la incrustación plana del grafo.[16]​

Un grafo Halin sin ningún ciclo 8. Una construcción similar permite evitar cualquier longitud de ciclo par.[17]​

Por lo tanto, muchos problemas de optimización de grafos que son NP-completos para grafos planos arbitrarios, como encontrar un conjunto independiente máximo, pueden resolverse en tiempo lineal en grafos Halin utilizando programación dinámica[18]​ o el teorema de Courcelle, o en algunos casos (como la construcción de ciclos Hamiltonianos) mediante algoritmos directos.[19]​ Sin embargo, es NP-completo encontrar el mayor subgrafo de Halin de un grafo dado, probar si existe un subgrafo de Halin que incluya todos los vértices de un grafo dado, o probar si un grafo dado es un subgrafo de un grafo de Halin mayor.[20]​

Historia

En 1971, Halin introdujo los grafos de Halin como una clase de grafos mínimamente conectados por 3 vértices: para cada arista en el grafo, la eliminación de esa arista reduce la conectividad del grafo.[2]​ Estos grafos ganaron importancia con el descubrimiento de que muchos problemas algorítmicos que eran computacionalmente inviables para grafos planos arbitrarios podían resolverse eficientemente en ellos.[15]​[9]​Más tarde se explicó que este hecho era consecuencia de su poca anchura de árboles y de metateoremas algorítmicos como el teorema de Courcelle, que proporciona soluciones eficientes a estos problemas en cualquier grafo de poca anchura de árboles .[19]​[20]​

Antes del trabajo de Halin sobre estos grafos, los problemas de enumeración de grafos relativos a los grafos cúbicos (o 3-regulares) de Halin fueron estudiados en 1856 por Thomas Kirkman[3]​ y en 1965 por Hans Rademacher. Rademacher denomina a estos grafos poliedros basados. Los define como los grafos poliédricos cúbicos con f caras en los que una de las caras tiene f - 1 lados.[21]​ Los grafos que se ajustan a esta definición son exactamente los grafos cúbicos de Halin.[22]​

Inspirándose en el hecho de que tanto los grafos de Halin como los grafos planares de 4 vértices conectados contienen ciclos hamiltonianos, Lovász y Plummer (1974) conjeturaran que todo grafo planar de 4 vértices conectados contiene un subgrafo de Halin que abarca todos los vértices del grafo mayor. La conjetura de Lovász-Plummer permaneció abierta hasta 2015, cuando se publicó una construcción para infinitos contraejemplos.[23]​

Los grafos de Halin a veces también se denominan árboles bordeados[11]​ o poliedros sin techo,[9]​ aunque estos nombres son ambiguos. Algunos autores utilizan el nombre "árboles bordeados" para referirse a los grafos planos formados a partir de árboles mediante la conexión de las hojas en un ciclo, pero sin requerir que los vértices internos del árbol tengan grado tres o más.[24]​ Y al igual que "poliedros basados", el nombre "poliedros sin techo" también puede referirse a los grafos de Halin cúbicos.[22]​Los poliedros convexos cuyos grafos son grafos de Halin también han sido llamados cúpulas.[25]​

Referencias

  1. ↑ a b c Encyclopaedia of Mathematics, first Supplementary volume, 1988, ISBN 0-7923-4709-9, p. 281, article "Halin Graph", and references therein.
  2. ↑ a b Halin, R. (1971), "Studies on minimally n-connected graphs", Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), London: Academic Press, pp. 129–136, MR 0278980
  3. ↑ a b Kirkman, Th. P. (1856), "On the enumeration of x-edra having triedral summits and an (x − 1)-gonal base", Philosophical Transactions of the Royal Society of London, 146: 399–411, doi:10.1098/rstl.1856.0018, JSTOR 108592
  4. ↑ Cornuéjols, Naddef y Pulleyblank (1983): "If T is a star, i.e., a single node v joined to n other nodes, then↵H is called a wheel and is the simplest type of Halin graph."
  5. ↑ See Sysło y Proskurowski (1983), Prop. 4.3, p. 254, which identifies the triangular prism as the unique graph with exactly three cycles that can be the outer cycle of a realization as a Halin graph.
  6. ↑ Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), "Computer investigation of cubic graphs", Eindhoven University of Technology Research Portal, EUT report, 76-WSK-01, Dept. of Mathematics and Computing Science, Eindhoven University of Technology
  7. ↑ Weisstein, Eric W. «Halin Graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
  8. ↑ Aichholzer, Oswin; Cheng, Howard; Devadoss, Satyan L.; Hackl, Thomas; Huber, Stefan; Li, Brian; Risteski, Andrej (2012), "What makes a tree a straight skeleton?" (PDF), Proceedings of the 24th Canadian Conference on Computational Geometry (CCCG'12)
  9. ↑ a b c Cornuéjols, G.; Naddef, D.; Pulleyblank, W. R. (1983), "Halin graphs and the travelling salesman problem", Mathematical Programming, 26 (3): 287–294, doi:10.1007/BF02591867, S2CID 26278382
  10. ↑ See the proof of Theorem 10 in Wang, Weifan; Bu, Yuehua; Montassier, Mickaël; Raspaud, André (2012), "On backbone coloring of graphs", Journal of Combinatorial Optimization, 23 (1): 79–93, doi:10.1007/s10878-010-9342-6, MR 2875236, S2CID 26975523: "Since G contains a 3-cycle consisting of one inner vertex and two outer vertices, G is not a bipartite graph."
  11. ↑ a b Skowrońska, Mirosława (1985), "The pancyclicity of Halin graphs and their exterior contractions", in Alspach, Brian R.; Godsil, Christopher D. (eds.), Cycles in Graphs, Annals of Discrete Mathematics, vol. 27, Elsevier Science Publishers B.V., pp. 179–194.
  12. ↑ Wang, Shu-Dong; Chen, Dong-Ling; Pang, Shan-Chen (2002), "The incidence coloring number of Halin graphs and outerplanar graphs", Discrete Mathematics, 256 (1–2): 397–405, doi:10.1016/S0012-365X(01)00302-8, MR 1927561.
  13. ↑ Shiu, W. C.; Sun, P. K. (2008), "Invalid proofs on incidence coloring", Discrete Mathematics, 308 (24): 6575–6580, doi:10.1016/j.disc.2007.11.030, MR 2466963.
  14. ↑ Fomin, Fedor V.; Thilikos, Dimitrios M. (2006), "A 3-approximation for the pathwidth of Halin graphs", Journal of Discrete Algorithms, 4 (4): 499–510, doi:10.1016/j.jda.2005.06.004, MR 2577677.
  15. ↑ a b Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, vol. 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635.
  16. ↑ Eppstein, David (2016), "Simple recognition of Halin graphs and their generalizations", Journal of Graph Algorithms and Applications, 20 (2): 323–346, arXiv:1502.05334, doi:10.7155/jgaa.00395, S2CID 9525753.
  17. ↑ Malkevitch, Joseph (1978), "Cycle lengths in polytopal graphs", Theory and Applications of Graphs (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), Lecture Notes in Mathematics, vol. 642, Berlin: Springer, pp. 364–370, doi:10.1007/BFb0070393, ISBN 978-3-540-08666-6, MR 0491287
  18. ↑ Bodlaender, Hans (1988), Planar graphs with bounded treewidth (PDF), Technical Report RUU-CS-88-14, Department of Computer Science, Utrecht University, archivado del original (PDF) 2004-07-28.
  19. ↑ a b Bodlaender, Hans (1988), "Dynamic programming on graphs with bounded treewidth", Proceedings of the 15th International Colloquium on Automata, Languages and Programming, Lecture Notes in Computer Science, vol. 317, Springer-Verlag, pp. 105–118, doi:10.1007/3-540-19488-6_110, hdl:1874/16258, ISBN 978-3540194880.
  20. ↑ a b Horton, S. B.; Parker, R. Gary (1995), "On Halin subgraphs and supergraphs", Discrete Applied Mathematics, 56 (1): 19–35, doi:10.1016/0166-218X(93)E0131-H, MR 1311302.
  21. ↑ Rademacher, Hans (1965), "On the number of certain types of polyhedra", Illinois Journal of Mathematics, 9 (3): 361–380, doi:10.1215/ijm/1256068140, MR 0179682.
  22. ↑ a b Lovász, L.; Plummer, M. D. (1974), "On a family of planar bicritical graphs", Combinatorics (Proc. British Combinatorial Conf., Univ. Coll. Wales, Aberystwyth, 1973), London: Cambridge Univ. Press, pp. 103–107. London Math. Soc. Lecture Note Ser., No. 13, MR 0351915.
  23. ↑ Chen, Guantao; Enomoto, Hikoe; Ozeki, Kenta; Tsuchiya, Shoichi (2015), "Plane triangulations without a spanning Halin subgraph: counterexamples to the Lovász-Plummer conjecture on Halin graphs", SIAM Journal on Discrete Mathematics, 29 (3): 1423–1426, doi:10.1137/140971610, MR 3376776.
  24. ↑ Skowrońska, M.; Sysło, M. M. (1987), "Hamiltonian cycles in skirted trees", Proceedings of the International Conference on Combinatorial Analysis and its Applications (Pokrzywna, 1985), Zastos. Mat., 19 (3–4): 599–610 (1988), MR 0951375
  25. ↑ Demaine, Erik D.; Demaine, Martin L.; Uehara, Ryuhei (2013), "Zipper unfolding of domes and prismoids", Proceedings of the 25th Canadian Conference on Computational Geometry (CCCG 2013), Waterloo, Ontario, Canada, August 8–10, 2013, pp. 43–48.

Enlaces externos

  • Grafos de Halin, Sistema de información sobre inclusiones de clases de grafos.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons Attribution-Share Alike 4.0. Pueden aplicarse cláusulas adicionales a los archivos multimedia.