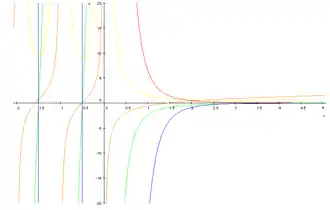
Diferentes gráficas de la función poligamma a lo largo del eje x . En naranja, para m =0, en amarillo, para m =1, en verde, para m =2, en rojo, para m =3 y en azul para m =4. En matemática , la función poligamma de orden m se define como la (m+1) -ésima derivada del logaritmo de la función gamma :
ψ
(
m
)
(
x
)
=
(
d
d
x
)
m
ψ
(
x
)
=
(
d
d
x
)
m
+
1
log
Γ
(
x
)
{\displaystyle \psi ^{(m)}(x)=\left({\frac {d}{dx}}\right)^{m}\psi (x)=\left({\frac {d}{dx}}\right)^{m+1}\log \Gamma (x)}
donde
ψ
(
x
)
=
ψ
0
(
x
)
=
Γ
′
(
x
)
Γ
(
x
)
{\displaystyle \psi (x)=\psi ^{0}(x)={\frac {\Gamma '(x)}{\Gamma (x)}}}
es la función digamma .
Representaciones
La función poligamma puede ser representada en forma de integral como
ψ
(
m
)
(
z
)
=
(
−
1
)
m
+
1
∫
0
∞
t
m
e
−
z
t
1
−
e
−
t
d
t
{\displaystyle \psi ^{(m)}(z)=(-1)^{m+1}\int _{0}^{\infty }{\frac {t^{m}e^{-zt}}{1-e^{-t}}}dt}
que se cumple para Re z >0 y m > 0. Para m = 0 véase la definición de función digamma .
Relación de recurrencia
Esta tiene la siguiente relación de recurrencia
ψ
(
m
)
(
z
+
1
)
=
ψ
(
m
)
(
z
)
+
(
−
1
)
m
m
!
z
−
(
m
+
1
)
.
{\displaystyle \psi ^{(m)}(z+1)=\psi ^{(m)}(z)+(-1)^{m}\;m!\;z^{-(m+1)}.}
Teorema de multiplicación
El teorema de multiplicación proporciona la siguiente fórmula
k
m
ψ
(
m
−
1
)
(
k
z
)
=
∑
n
=
0
k
−
1
ψ
(
m
−
1
)
(
z
+
n
k
)
{\displaystyle k^{m}\psi ^{(m-1)}(kz)=\sum _{n=0}^{k-1}\psi ^{(m-1)}\left(z+{\frac {n}{k}}\right)}
para
m
>
1
{\displaystyle m>1}
m
=
0
{\displaystyle m=0}
función digamma :
k
(
ψ
(
k
z
)
−
log
(
k
)
)
=
∑
n
=
0
k
−
1
ψ
(
z
+
n
k
)
.
{\displaystyle k(\psi (kz)-\log(k))=\sum _{n=0}^{k-1}\psi \left(z+{\frac {n}{k}}\right).}
La función poligamma tiene la siguiente representación en forma de serie
ψ
(
m
)
(
z
)
=
(
−
1
)
m
+
1
m
!
∑
k
=
0
∞
1
(
z
+
k
)
m
+
1
{\displaystyle \psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\sum _{k=0}^{\infty }{\frac {1}{(z+k)^{m+1}}}}
que se cumple para m > 0 y cualquier número complejo z que no sea igual a un número negativo . Esta representación puede ser escrita de manera más compacta en términos de la función zeta de Hurwitz como
ψ
(
m
)
(
z
)
=
(
−
1
)
m
+
1
m
!
ζ
(
m
+
1
,
z
)
.
{\displaystyle \psi ^{(m)}(z)=(-1)^{m+1}\;m!\;\zeta (m+1,z).}
Alternativamente, la función zeta de Hurwitz puede ser entendida como la generalización de la función poligamma a un orden no entero arbitrario.
Una serie más se puede permitir a las funciones poligamma. como la dada por Oskar Schlömilch ,
1
/
Γ
(
z
)
=
z
e
γ
z
∏
n
=
1
∞
(
1
+
z
n
)
e
−
z
/
n
{\displaystyle 1/\Gamma (z)=z\;{\mbox{e}}^{\gamma z}\;\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)\;{\mbox{e}}^{-z/n}}
teorema de factorización de Weierstrass .Por lo tanto, la función gamma puede ser definida ahora como:
Γ
(
z
)
=
e
−
γ
z
z
∏
n
=
1
∞
(
1
+
z
n
)
−
1
e
z
/
n
{\displaystyle \Gamma (z)={\frac {{\mbox{e}}^{-\gamma z}}{z}}\;\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}\;{\mbox{e}}^{z/n}}
De esta manera, el logaritmo natural de la función gamma es fácilmente representable:
ln
Γ
(
z
)
=
−
γ
z
−
ln
(
z
)
+
∑
n
=
1
∞
(
z
n
−
ln
(
1
+
z
n
)
)
{\displaystyle \ln \Gamma (z)=-\gamma z-\ln(z)+\sum _{n=1}^{\infty }\left({\frac {z}{n}}-\ln(1+{\frac {z}{n}})\right)}
Finalmente, se llega a una representación en forma de sumatorio para la función poligamma:
ψ
(
n
)
(
z
)
=
d
n
+
1
d
z
n
+
1
ln
Γ
(
z
)
=
−
γ
δ
n
0
−
(
−
1
)
n
n
!
z
n
+
1
+
∑
k
=
1
∞
(
1
k
δ
n
0
−
(
−
1
)
n
n
!
(
k
+
z
)
n
+
1
)
{\displaystyle \psi ^{(n)}(z)={\frac {d^{n+1}}{dz^{n+1}}}\ln \Gamma (z)=-\gamma \delta _{n0}\;-\;{\frac {(-1)^{n}n!}{z^{n+1}}}\;+\;\sum _{k=1}^{\infty }\left({\frac {1}{k}}\delta _{n0}\;-\;{\frac {(-1)^{n}n!}{(k+z)^{n+1}}}\right)}
Donde
δ
n
0
{\displaystyle \delta _{n0}}
delta de Kronecker .
Serie de Taylor
La serie de Taylor en z = 1 es
ψ
(
m
)
(
z
+
1
)
=
∑
k
=
0
∞
(
−
1
)
m
+
k
+
1
(
m
+
k
)
!
ζ
(
m
+
k
+
1
)
z
k
k
!
,
{\displaystyle \psi ^{(m)}(z+1)=\sum _{k=0}^{\infty }(-1)^{m+k+1}(m+k)!\;\zeta (m+k+1)\;{\frac {z^{k}}{k!}},}
que converge para todo |z | < 1. Aquí, ζ es la función zeta de Riemann . Esta serie se deriva de la correspondiente serie de Taylor para la función zeta de Hurwitz. Esta serie se puede utilizar para obtener un número de series zeta racionales.
Véase también
Referencias
Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions , (1964) Dover Publications , New York. ISBN 978-0-486-61272-0 . See section §6.4
Enlaces externos