Función cuasiconvexa

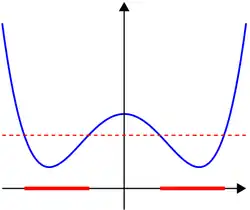
En matemáticas, una función cuasiconvexa es una función con valores reales definida en un intervalo o en un subconjunto convexo de un espacio vectorial real, tal que la imagen inversa de cualquier conjunto de la forma ${\displaystyle (-\infty ,a)}$ es un conjunto convexo. Para una función de una sola variable, a lo largo de cualquier tramo de la curva, el punto más alto es uno de los extremos. El negativo de una función cuasiconvexa se denomina cuasicóncavo.

La cuasiconvexidad es una propiedad más general que la convexidad, ya que todas las funciones convexas también son cuasiconvexas, pero no todas las funciones cuasiconvexas son convexas. Las funciones univariadas unimodales son cuasiconvexas o cuasicóncavas; sin embargo, este no es necesariamente el caso para funciones con múltiples argumentos. Por ejemplo, la función de Rosenbrock bidimensional es unimodal pero no cuasiconvexa, y las funciones con conjuntos de subnivel estrellados pueden ser unimodales sin ser cuasiconvexas.

Una función ${\displaystyle f:S\to \mathbb {R} }$ definida en un subconjunto convexo ${\displaystyle S}$ de un espacio vectorial real es cuasiconvexa si para todo ${\displaystyle x,y\in S}$ y ${\displaystyle \lambda \in [0,1]}$ se cumple:

${\displaystyle f(\lambda x+(1-\lambda )y)\leq \max {\big \{}f(x),f(y){\big \}}.}$

En palabras, si ${\displaystyle f}$ es tal que siempre es cierto que un punto directamente entre otros dos puntos no da un valor de la función mayor que el de ambos puntos, entonces ${\displaystyle f}$ es cuasiconvexa. Nótese que los puntos ${\displaystyle x}$ e ${\displaystyle y}$, y el punto directamente entre ellos, pueden ser puntos en una línea o, más generalmente, puntos en un espacio n-dimensional.

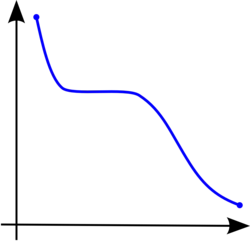
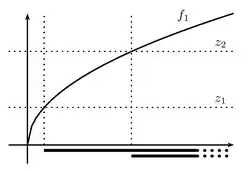
Una forma alternativa (ver introducción) de definir una función cuasiconvexa ${\displaystyle f(x)}$ es exigir que cada conjunto de subnivel ${\displaystyle S_{\alpha }(f)=\{x\mid f(x)\leq \alpha \}}$ sea un conjunto convexo.

Si además

${\displaystyle f(\lambda x+(1-\lambda )y)<\max {\big \{}f(x),f(y){\big \}}}$

para todo ${\displaystyle x\neq y}$ y ${\displaystyle \lambda \in (0,1)}$, entonces ${\displaystyle f}$ es estrictamente cuasiconvexa. Es decir, la cuasiconvexidad estricta requiere que un punto directamente entre otros dos puntos dé un valor de la función menor que uno de los otros puntos.

Una función cuasicóncava es una función cuyo negativo es cuasiconvexo, y una función estrictamente cuasicóncava es una función cuyo negativo es estrictamente cuasiconvexo. Equivalentemente, una función ${\displaystyle f}$ es cuasicóncava si

${\displaystyle f(\lambda x+(1-\lambda )y)\geq \min {\big \{}f(x),f(y){\big \}}.}$

y estrictamente cuasicóncava si

${\displaystyle f(\lambda x+(1-\lambda )y)>\min {\big \{}f(x),f(y){\big \}}}$

Una función (estrictamente) cuasiconvexa tiene conjuntos de nivel inferior (estrictamente) convexos, mientras que una función (estrictamente) cuasicóncava tiene conjuntos de nivel superior (estrictamente) convexos.

Una función que es tanto cuasiconvexa como cuasicóncava se denomina cuasilineal.

Un caso particular de cuasi-concavidad, si ${\displaystyle S\subset \mathbb {R} }$, es la unimodalidad, en la que existe un valor localmente máximo.

Las funciones cuasiconvexas tienen aplicaciones en análisis matemático, en optimización matemática y en teoría de juegos y economía.

En optimización no lineal, la programación cuasiconvexa estudia métodos iterativos que convergen a un mínimo (si existe) para funciones cuasiconvexas. La programación cuasiconvexa es una generalización de la programación convexa.^[1]​ La programación cuasiconvexa se utiliza en la solución de problemas duales "sustitutos", cuyos biduales proporcionan cierres cuasiconvexos del problema primal, que por lo tanto ofrecen cotas más ajustadas que los cierres convexos proporcionados por problemas duales lagrangianos.^[2]​ En teoría, los problemas de programación cuasiconvexa y convexa pueden resolverse en un tiempo razonable, donde el número de iteraciones crece como un polinomio en la dimensión del problema (y en el recíproco del error de aproximación tolerado);^[3]​ sin embargo, tales métodos teóricamente "eficientes" utilizan reglas de tamaño de paso de "series divergentes", desarrolladas originalmente para los métodos del subgradiente clásicos. Los métodos clásicos del subgradiente que utilizan reglas de series divergentes son mucho más lentos que los métodos modernos de minimización convexa, como los métodos de proyección del subgradiente, los métodos de haz de descenso y los métodos de filtro no suaves.

En microeconomía, las funciones de utilidad cuasicóncavas implican que los consumidores tienen preferencias convexas. Las funciones cuasiconvexas también son importantes en la teoría de juegos, la organización industrial y la teoría del equilibrio general, particularmente para aplicaciones del teorema minimax de Sion. Generalizando un teorema minimax de John von Neumann, el teorema de Sion también se utiliza en la teoría de ecuaciones diferenciales parciales.

• El máximo de funciones cuasiconvexas (es decir, ${\displaystyle f=\max \left\lbrace f_{1},\ldots ,f_{n}\right\rbrace }$) es cuasiconvexo. De manera similar, el máximo de funciones estrictamente cuasiconvexas es estrictamente cuasiconvexo.^[4]​ De manera similar, el mínimo de funciones cuasicóncavas es cuasicóncavo, y el mínimo de funciones estrictamente cuasicóncavas es estrictamente cuasicóncavo.
• Composición con una función no decreciente: ${\displaystyle g:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ cuasiconvexa, ${\displaystyle h:\mathbb {R} \rightarrow \mathbb {R} }$ no decreciente, entonces ${\displaystyle f=h\circ g}$ es cuasiconvexa. De manera similar, si ${\displaystyle g:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ es cuasicóncava, ${\displaystyle h:\mathbb {R} \rightarrow \mathbb {R} }$ no decreciente, entonces ${\displaystyle f=h\circ g}$ es cuasicóncava.
• Minimización (es decir, ${\displaystyle f(x,y)}$ cuasiconvexa, ${\displaystyle C}$ conjunto convexo, entonces ${\displaystyle h(x)=\inf _{y\in C}f(x,y)}$ es cuasiconvexa).

• La suma de funciones cuasiconvexas definidas en el mismo dominio no necesariamente es cuasiconvexa: en otras palabras, si ${\displaystyle f(x),g(x)}$ son cuasiconvexas, entonces ${\displaystyle (f+g)(x)=f(x)+g(x)}$ no necesariamente es cuasiconvexa.
• La suma de funciones cuasiconvexas definidas en dominios diferentes (es decir, si ${\displaystyle f(x),g(y)}$ son cuasiconvexas, ${\displaystyle h(x,y)=f(x)+g(y)}$) no necesariamente es cuasiconvexa. Tales funciones se denominan "aditivamente descompuestas" en economía y "separables" en optimización matemática.

• Toda función convexa es cuasiconvexa.
• Una función cóncava puede ser cuasiconvexa. Por ejemplo, ${\displaystyle x\mapsto \log(x)}$ es tanto cóncava como cuasiconvexa.
• Cualquier función monótona es tanto cuasiconvexa como cuasicóncava. Más generalmente, una función que decrece hasta un punto y luego crece a partir de ese punto es cuasiconvexa (comparar con unimodalidad).
• La función suelo ${\displaystyle x\mapsto \lfloor x\rfloor }$ es un ejemplo de función cuasiconvexa que no es ni convexa ni continua.

• Función convexa
• Función cóncava
• Función logarítmicamente cóncava
• Pseudoconvexidad en el sentido de varias variables complejas (no convexidad generalizada)
• Función pseudoconvexa
• Función invexa
• Concavificación