Estimación de Espaciado Máximo

En estadística, la estimación de Espaciado Máximo (MSE o MSP), o estimación del producto máximo del espaciamiento (MPS), es un método para estimar los parámetros de un modelo estadístico univariante.^[1]​ El método requiere la maximización de la media geométrica de los espaciamientos en los datos, que son las diferencias entre los valores de la función de distribución acumulativa en puntos de datos vecinos.

El concepto que subyace al método se basa en la transformada integral de probabilidad, en el sentido de que un conjunto de muestras aleatorias independientes derivadas de cualquier variable aleatoria deberían, en promedio, estar uniformemente distribuidas con respecto a la función de distribución acumulativa de la variable aleatoria. El método MPS elige los valores de los parámetros que hacen que los datos observados sean lo más uniformes posible, de acuerdo con una medida cuantitativa específica de uniformidad.

Uno de los métodos más comunes para estimar los parámetros de una distribución a partir de los datos, el método de máxima verosimilitud (MLE), puede fallar en varios casos, como cuando se trata de ciertas mezclas de distribuciones continuas.^[2]​ En estos casos, el método de estimación de máximo espaciamiento puede tener éxito.

Aparte de su uso en matemáticas puras y estadística, las aplicaciones de prueba del método se han reportado utilizando datos de campos como la hidrología,^[3]​econometría,^[4]​ imágenes de resonancia magnética,^[5]​y otros. ^[6]​

El método MSE fue derivado independientemente por Russel Cheng y Nik Amin en el Instituto de Ciencia y Tecnología de la Universidad de Gales, y Bo Ranneby en la Universidad Sueca de Ciencias Agrícolas.^[2]​Los autores explicaron que debido a la transformada integral de probabilidad en el parámetro verdadero, el "espaciado" entre cada observación debería estar uniformemente distribuido. Esto implicaría que la diferencia entre los valores de la función de distribución acumulativa en observaciones consecutivas debería ser igual. Este es el caso que maximiza la media geométrica de dichos espaciamientos, por lo que resolviendo para los parámetros que maximizan la media geométrica se conseguiría el "mejor" ajuste definido de esta forma. Ranneby (1984) justificó el método demostrando que es un estimador de la divergencia de Kullback-Leibler, similar a la estimación de máxima verosimilitud, pero con propiedades más robustas para algunas clases de problemas.

Hay ciertas distribuciones, especialmente aquellas con tres o más parámetros, cuyas verosimilitudes pueden llegar a ser infinitas a lo largo de ciertas trayectorias en el espacio de parámetros. El uso de la máxima verosimilitud para estimar estos parámetros a menudo se rompe, con un parámetro que tiende al valor específico que hace que la verosimilitud sea infinita, haciendo que los otros parámetros sean inconsistentes. Sin embargo, el método de los espacios máximos, al depender de la diferencia entre los puntos de la función de distribución acumulativa y no de los puntos de verosimilitud individuales, no presenta este problema y arrojará resultados válidos en una gama mucho más amplia de distribuciones.^[1]​

Las distribuciones que tienden a presentar problemas de verosimilitud suelen ser las utilizadas para modelizar fenómenos físicos. Hall & al. (2004) intentan analizar métodos de alivio de inundaciones, lo que requiere modelos precisos de los efectos de las inundaciones fluviales. Las distribuciones que mejor modelizan estos efectos son los modelos de tres parámetros, que adolecen del problema de probabilidad infinita descrito anteriormente, lo que llevó a Hall a investigar el procedimiento de espaciado máximo. Wong & Li (2006), al comparar el método con el de máxima verosimilitud, utilizan varios conjuntos de datos que van desde un conjunto sobre las edades más avanzadas al morir en Suecia entre 1905 y 1958 hasta un conjunto que contiene las velocidades máximas anuales del viento.

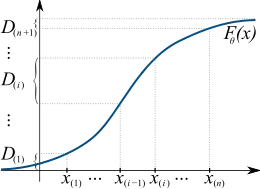
Dada una muestra aleatoria iid {x1, ..., xn} de tamaño n de una distribución univariante con función de distribución acumulativa continua F(x;θ0), donde θ0 ∈ Θ es un parámetro desconocido que debe estimarse, sea {x(1), ..., x(n)} la muestra ordenada correspondiente, es decir, el resultado de ordenar todas las observaciones de menor a mayor. Por conveniencia, denotemos también x(0) = -∞ y x(n+1) = +∞.

Defina los espacios como los "huecos" entre los valores de la función de distribución en puntos ordenados adyacentes:^[7]​

$${\displaystyle D_{i}(\theta )=F(x_{(i)};\,\theta )-F(x_{(i-1)};\,\theta ),\quad i=1,\ldots ,n+1.}$$

A continuación, el estimador de espaciamiento máximo de θ0 se define como un valor que maximiza el logaritmo de la media geométrica de los espaciamientos de las muestras:

$${\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\;S_{n}(\theta ),\quad {\text{where }}\ S_{n}(\theta )=\ln \!\!{\sqrt[{n+1}]{D_{1}D_{2}\cdots D_{n+1}}}={\frac {1}{n+1}}\sum _{i=1}^{n+1}\ln {D_{i}}(\theta ).}$$

Por la desigualdad de medias aritméticas y geométricas, la función Sn(θ) está acotada desde arriba por -ln(n+1), y por tanto el máximo tiene que existir al menos en el sentido del sumo.

Obsérvese que algunos autores definen la función Sn(θ) de forma algo diferente. En particular, Ranneby (1984) multiplica cada Di por un factor de (n+1), mientras que Cheng & Stephens (1989) omiten el factor 1⁄n+1 delante de la suma y añaden el signo "-"para convertir la maximización en minimización. Como se trata de constantes con respecto a θ, las modificaciones no alteran la localización del máximo de la función Sn.

En esta sección se presentan dos ejemplos de cálculo del estimador del espaciado máximo.

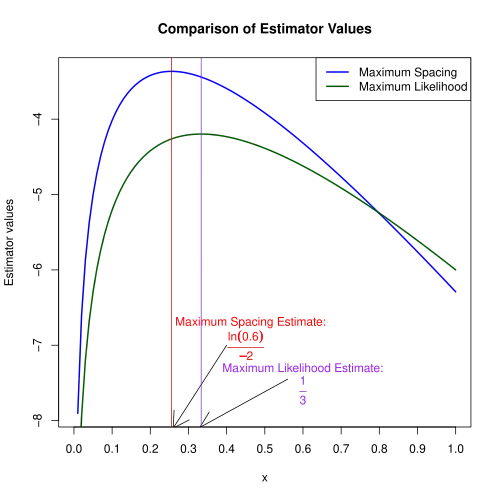
Supongamos que dos valores x(1) = 2, x(2) = 4 fueron muestreados a partir de la distribución exponencial F(x;λ) = 1 - e-xλ, x ≥ 0 con parámetro desconocido λ > 0. Para construir el MSE tenemos que encontrar primero los espaciamientos:

El proceso continúa encontrando la λ que maximiza la media geométrica de la columna "diferencia". Usando la convención que ignora tomar la (n+1)raíz, esto se convierte en la maximización del siguiente producto: (1 - e-2λ) - (e-2λ - e-4λ) - (e-4λ). Dejando μ = e-2λ, el problema se convierte en encontrar el máximo de μ5-2μ4+μ3. Diferenciando, la μ tiene que satisfacer 5μ4-8μ3+3μ2 = 0. Esta ecuación tiene raíces 0, 0,6 y 1. Como μ es en realidad e-2λ, tiene que ser mayor que cero pero menor que uno. Por lo tanto, la única solución aceptable es 𝜇=0,6⇒𝜆MSE=ln 0,6-2≈0,255,

que corresponde a una distribución exponencial con una media de 1⁄λ ≈ 3,915. Por comparación, la estimación de máxima verosimilitud de λ es la inversa de la media muestral, 3, por lo que λMLE = ⅓ ≈ 0,333.

Supongamos que {x(1), ..., x(n)} es la muestra ordenada de una distribución uniforme U(a,b) con extremos a y b desconocidos. La función de distribución acumulativa es F(x;a,b) = (x-a)/(b-a) cuando x∈[a,b]. Por lo tanto, los espaciamientos individuales vienen dados por:

$${\displaystyle D_{1}={\frac {x_{(1)}-a}{b-a}},\ \ D_{i}={\frac {x_{(i)}-x_{(i-1)}}{b-a}}\ {\text{for }}i=2,\ldots ,n,\ \ D_{n+1}={\frac {b-x_{(n)}}{b-a}}\ \ }$$

Calculando la media geométrica y tomando después el logaritmo, el estadístico Sn será igual a:$${\displaystyle S_{n}(a,b)={\tfrac {\ln(x_{(1)}-a)}{n+1}}+{\tfrac {\sum _{i=2}^{n}\ln(x_{(i)}-x_{(i-1)})}{n+1}}+{\tfrac {\ln(b-x_{(n)})}{n+1}}-\ln(b-a)}$$ Aquí sólo tres términos dependen de los parámetros a y b. Diferenciando con respecto a esos parámetros y resolviendo el sistema lineal resultante, las estimaciones de espaciado máximo serán${\displaystyle {\hat {a}}={\frac {nx_{(1)}-x_{(n)}}{n-1}},\ \ {\hat {b}}={\frac {nx_{(n)}-x_{(1)}}{n-1}}.}$En comparación, las estimaciones de máxima verosimilitud para este problema 𝑎^=𝑥(1) y 𝑏^=𝑥(𝑛) están sesgadas y tienen un error cuadrático medio más alto.

El estimador del espaciado máximo es un estimador coherente en el sentido de que converge en probabilidad al valor verdadero del parámetro, θ0, a medida que el tamaño de la muestra aumenta hasta el infinito.^[1]​ La coherencia de la estimación del espaciado máximo se mantiene en condiciones mucho más generales que en el caso de los estimadores de máxima verosimilitud. En particular, en los

Densidad

Distribución

Gráfico de una función de densidad "en forma de J" y su distribución correspondiente. Un Weibull desplazado con un parámetro de escala de 15, un parámetro de forma de 0,5 y un parámetro de localización de 10. La densidad se aproxima asintóticamente al infinito a medida que x se acerca a 10, lo que hace que las estimaciones de otros parámetros sean inconsistentes. La densidad se aproxima asintóticamente al infinito a medida que x se aproxima a 10, lo que hace que las estimaciones de los otros parámetros sean inconsistentes. Nótese que no hay punto de inflexión en la gráfica de la distribución.

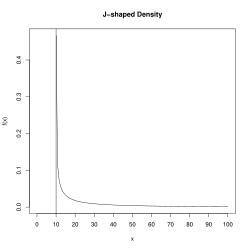
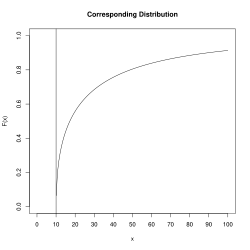
casos en los que la distribución subyacente tiene forma de J, la máxima verosimilitud fallará mientras que el MSE tiene éxito.^[2]​ Un ejemplo de una densidad con forma de J es la distribución de Weibull, concretamente una Weibull desplazada, con un parámetro de forma inferior a 1. La densidad tenderá a infinito a medida que x se acerque al parámetro de ubicación, lo que hará que las estimaciones de los demás parámetros sean incoherentes.

Los estimadores de máximo espaciado son también al menos tan asintóticamente eficientes como los estimadores de máxima verosimilitud, cuando existen estos últimos. Sin embargo, los MSE pueden existir en casos en los que los MLE no.^[1]​

Los estimadores de espaciado máximo son sensibles a las observaciones muy espaciadas, y especialmente a los empates.^[8]​

Dado$${\displaystyle X_{i+k}=X_{i+k-1}=\cdots =X_{i},\,}$$obtenemos $${\displaystyle D_{i+k}(\theta )=D_{i+k-1}(\theta )=\cdots =D_{i+1}(\theta )=0.\,}$$Cuando los empates se deben a observaciones múltiples, los espaciamientos repetidos (los que de otro modo serían cero) deben sustituirse por la probabilidad correspondiente.^[1]​ Es decir, se debe sustituir 𝑓𝑖(𝜃) por 𝐷𝑖(𝜃), $${\displaystyle \lim _{x_{i}\to x_{i-1}}{\frac {\int _{x_{i-1}}^{x_{i}}f(t;\theta )\,dt}{x_{i}-x_{i-1}}}=f(x_{i-1},\theta )=f(x_{i},\theta ),}$$Desde ${\displaystyle x_{i}=x_{i-1}}$

Cuando los empates se deben a un error de redondeo, Cheng & Stephens (1989) sugieren otro método para eliminar los efectos. ^{[Notas 1]}​Dadas r observaciones empatadas de xi a xi+r-1, dejemos que δ represente el error de redondeo. Todos los valores verdaderos deberían caer en el rango 𝑥±𝛿. Los puntos correspondientes de la distribución deben estar comprendidos entre 𝑦 𝐿=𝐹(𝑥-𝛿,𝜃^) y 𝑦𝑈=𝐹(𝑥+𝛿,𝜃^). Cheng y Stephens sugieren asumir que los valores redondeados están uniformemente espaciados en este intervalo, definiendo

$${\displaystyle D_{j}={\frac {y_{U}-y_{L}}{r-1}}\quad (j=i+1,\ldots ,i+r-1).}$$

El método MSE también es sensible a la agrupación secundaria.^[8]​ Un ejemplo de este fenómeno es cuando se cree que un conjunto de observaciones procede de una única distribución normal, pero en realidad procede de una mezcla de normales con diferentes medias. Un segundo ejemplo es cuando se cree que los datos proceden de una distribución exponencial, pero en realidad proceden de una distribución gamma. En este último caso, pueden producirse separaciones más pequeñas en la cola inferior. Un valor alto de M(θ) indicaría este efecto de agrupamiento secundario, y sugeriría que es necesario examinar los datos más detenidamente.^[8]​

El estadístico Sn(θ) es también una forma del estadístico de Moran o Moran-Darling, M(θ), que puede utilizarse para probar la bondad del ajuste.^{[Notas 2]}​ Se ha demostrado que el estadístico, cuando se define como:$${\displaystyle S_{n}(\theta )=M_{n}(\theta )=-\sum _{j=1}^{n+1}\ln {D_{j}(\theta )},}$$es asintóticamente normal, y que existe una aproximación chi-cuadrado para sa pequeños. En el caso de que conozcamos el verdadero parámetro 𝜃0, Cheng & Stephens (1989) muestran que el estadístico 𝑀𝑛(𝜃) tiene una distribución normal con:

$${\displaystyle {\begin{aligned}\mu _{M}&\approx (n+1)(\ln(n+1)+\gamma )-{\frac {1}{2}}-{\frac {1}{12(n+1)}},\\\sigma _{M}^{2}&\approx (n+1)\left({\frac {\pi ^{2}}{6}}-1\right)-{\frac {1}{2}}-{\frac {1}{6(n+1)}},\end{aligned}}}$$ donde γ es la constante de Euler-Mascheroni, que es aproximadamente 0,57722^{[Notas 3]}​

La distribución también puede aproximarse por la de 𝐴, donde $${\displaystyle A=C_{1}+C_{2}\chi _{n}^{2}\,,}$$

en la que $${\displaystyle {\begin{aligned}C_{1}&=\mu _{M}-{\sqrt {\frac {\sigma _{M}^{2}n}{2}}},\\C_{2}&={\sqrt {\frac {\sigma _{M}^{2}}{2n}}},\\\end{aligned}}}$$ y donde 𝜒𝑛2 sigue una distribución chi-cuadrado con 𝑛 grados de libertad. Por lo tanto, para probar la hipótesis ${\displaystyle H_{0}}$ de que una muestra aleatoria de 𝑛 valores proviene de la distribución ${\displaystyle F(x,\theta )}$, se puede calcular el estadístico ${\displaystyle T(\theta )={\frac {M(\theta )-C_{1}}{C_{2}}}}$. Entonces ${\displaystyle H_{0}}$debe ser rechazado con significación 𝛼 si el valor es mayor que el valor crítico de la distribución chi-cuadrado apropiada.^[8]​

Donde θ0 está siendo estimado por 𝜃^, Cheng & Stephens (1989) mostraron que ${\displaystyle S_{n}({\hat {\theta }})=M_{n}({\hat {\theta }})}$ tiene la misma media y varianza asintótica que en el caso conocido. Sin embargo, el estadístico de prueba a utilizar requiere la adición de un término de corrección de sesgo y es:$${\displaystyle T({\hat {\theta }})={\frac {M({\hat {\theta }})+{\frac {k}{2}}-C_{1}}{C_{2}}},}$$,donde 𝑘 es el número de parámetros en la estimación.

Ranneby & Ekström (1997) generalizaron el método MSE para aproximar otras medidas además de la medida de Kullback-Leibler. Ekström (1997) amplió aún más el método para investigar las propiedades de los estimadores utilizando espaciamientos de orden superior, donde un espaciamiento de orden m se definiría como ${\displaystyle F(X_{j+m})-F(X_{j})}$

Ranneby & al. (2005) discuten la extensión de los métodos de espaciado máximo al caso multivariante. Como no existe un orden natural para ${\displaystyle \mathbb {R} ^{k}(k>1)}$, discuten dos enfoques alternativos: un enfoque geométrico basado en celdas de Dirichlet y un enfoque probabilístico basado en una métrica de "bola vecina más cercana".

• Divergencia de Kullback-Leibler
• Máxima verosimilitud
• Distribución de probabilidad

1. ↑ Parece que hay algunos errores tipográficos menores en el documento. Por ejemplo, en la sección 4.2, la ecuación (4.1), el reemplazo de redondeo para ${\displaystyle D_{j}}$, no debería tener el término logarítmico. En la sección 1, ecuación (1.2), ${\displaystyle D_{j}}$ se define como el propio espaciado, y ${\displaystyle M(\theta )}$ es la suma negativa de los logaritmos de ${\displaystyle D_{j}}$. Si ${\displaystyle D_{j}}$ se registra en este paso, el resultado es siempre ≤ 0, ya que la diferencia entre dos puntos adyacentes en una distribución acumulativa es siempre ≤ 1, y estrictamente < 1 a menos que sólo haya dos puntos en los extremos. Además, en la sección 4.3, en la página 392, el cálculo muestra que es la varianza ${\displaystyle \textstyle {\tilde {\sigma ^{2}}}}$ que tiene MPS estimación de 6,87, no la desviación estándar ${\displaystyle \textstyle {\tilde {\sigma }}}$. - Editor
2. ↑ La literatura se refiere a las estadísticas relacionadas como estadísticas de Moran o Moran-Darling. Por ejemplo, Cheng y Stephens (1989) analizan la forma ${\displaystyle \scriptstyle M(\theta )=-\sum _{j=1}^{n+1}\log {D_{i}(\theta )}}$ donde ${\displaystyle \scriptstyle D_{i}(\theta )}$ se define como arriba. Wong y Li (2006) utilizan la misma forma también. Sin embargo, Beirlant y al. (2001) utiliza la forma ${\displaystyle \scriptstyle M_{n}=-\sum _{j=0}^{n}\ln {((n+1)(X_{n,i+1}-X_{n,i}))}}$, con el factor adicional de ${\displaystyle (n+1)}$ dentro de la suma registrada. Los factores adicionales harán una diferencia en términos de la media esperada y la varianza de la estadística. Por consistencia, este artículo continuará usando la forma Cheng & Amin/Wong & Li. -- Editor
3. ↑ Wong y Li (2006) omiten la constante de Euler-Mascheroni de su descripción. -- Editor

1. ↑ ^{a b c d e} Cheng y Amin (1983)
2. ↑ ^{a b c} Ranneby (1984)
3. ↑ Hall y al. (2004)
4. ↑ Anatolyev y Kosenok (2004)
5. ↑ Pieciak (2014)
6. ↑ Wong y Li (2006)
7. ↑ Pyke (1965)
8. ↑ ^{a b c d} Cheng y Stephens (1989)

• Anatolyev, Stanislav; Kosenok, Grigory (2005). "An alternative to maximum likelihood based on spacings" (PDF). Econometric Theory. 21 (2): 472–476. CiteSeerX 10.1.1.494.7340. doi:10.1017/S0266466605050255. S2CID 123004317. Archivado desde el original (PDF) el 2011-08-16. Consultado el 21 de enero de 2009.
• Beirlant, J.; Dudewicz, E.J.; Györfi, L.; van der Meulen, E.C. (1997). "Nonparametric entropy estimation: an overview" (PDF). International Journal of Mathematical and Statistical Sciences. 6 (1): 17–40. ISSN 1055-7490. Archivado desde el original (PDF) el 5 de mayo de 2005. Consultado el 31 de diciembre de 2008. Nota: el documento enlazado es una versión actualizada de 2001.
• Cheng, R.C.H.; Amin, N.A.K. (1983). "Estimating parameters in continuous univariate distributions with a shifted origin". Journal of the Royal Statistical Society, Series B. 45 (3): 394–403. doi:10.1111/j.2517-6161.1983.tb01268.x. ISSN 0035-9246. JSTOR 2345411.
• Cheng, R.C.H; Stephens, M. A. (1989). "A goodness-of-fit test using Moran's statistic with estimated parameters". Biometrika. 76 (2): 386–392. doi:10.1093/biomet/76.2.385.
• Ekström, Magnus (1997). "Generalized maximum spacing estimates". University of Umeå, Department of Mathematics. 6. ISSN 0345-3928. Archivado desde el original el 14 de febrero de 2007. Consultado el 30 de diciembre de 2008.
• Hall, M.J.; van den Boogaard, H.F.P.; Fernando, R.C.; Mynett, A.E. (2004). "The construction of confidence intervals for frequency analysis using resampling techniques". Hydrology and Earth System Sciences. 8 (2): 235–246. doi:10.5194/hess-8-235-2004. ISSN 1027-5606.
• Pieciak, Tomasz (2014). The maximum spacing noise estimation in single-coil background MRI data. IEEE International Conference on Image Processing. Paris. pp. 1743–1747. doi:10.1109/icip.2014.7025349.
• Pyke, Ronald (1965). "Spacings". Journal of the Royal Statistical Society, Series B. 27 (3): 395–449. doi:10.1111/j.2517-6161.1965.tb00602.x. ISSN 0035-9246. JSTOR 2345793.
• Ranneby, Bo (1984). "The maximum spacing method. An estimation method related to the maximum likelihood method". Scandinavian Journal of Statistics. 11 (2): 93–112. ISSN 0303-6898. JSTOR 4615946.
• Ranneby, Bo; Ekström, Magnus (1997). "Maximum spacing estimates based on different metrics". University of Umeå, Department of Mathematics. 5. ISSN 0345-3928. Archivado desde el original el 14 de febrero de 2007. Consultado el 30 de diciembre de 2008.
• Ranneby, Bo; Jammalamadakab, S. Rao; Teterukovskiy, Alex (2005). "The maximum spacing estimation for multivariate observations" (PDF). Journal of Statistical Planning and Inference. 129 (1–2): 427–446. doi:10.1016/j.jspi.2004.06.059. Consultado el 31 de diciembre de 2008.
• Wong, T.S.T; Li, W.K. (2006). "A note on the estimation of extreme value distributions using maximum product of spacings". Time series and related topics: in memory of Ching-Zong Wei. Institute of Mathematical Statistics Lecture Notes – Monograph Series. Beachwood, Ohio: Institute of Mathematical Statistic. pp. 272–283. arXiv:math/0702830v1. doi:10.1214/074921706000001102. ISBN 978-0-940600-68-3. S2CID 88516426.