Diseño experimental
El diseño experimental o diseño de experimentos, se refiere al proceso previo de planificación de un experimento con la finalidad de recopilar los datos adecuados, que posteriormente tratados de forma adecuada, permitan extraer conclusiones válidas y objetivas.[1] Para alcanzar estos objetivos y con el fin de que las conclusiones no estén sometidas a sesgo alguno, es muy conveniente e importante que el tratamiento de los datos obtenidos a partir del diseño sea llevado a cabo mediante métodos estadísticos. En realidad, cuando el problema involucra datos sujetos a errores experimentales, cosa muy habitual, la metodología estadística es el único enfoque objetivo para el análisis.
En su forma más simple, mediante el diseño experimental se busca predecir el resultado final de un experimento introduciendo un cambio en las precondiciones experimentales (p. e., temperatura, presión, etc.), representadas por una o más variables independientes, también conocidas como factores. De la elección adecuada de estos factores y de la magnitud de los mismos depende el resultado final del experimento. Este resultado recibe el nombre de "variable de respuesta" o respuesta experimental. El diseño experimental también puede buscar e identificar aquellas variables de control que deben mantenerse constantes para evitar que factores externos afecten a los resultados. Por consiguiente, el diseño experimental implica no solo la selección de variables independientes, dependientes y de control adecuadas, sino también la planificación de la ejecución del experimento en condiciones estadísticamente óptimas, dadas las limitaciones de los recursos disponibles.
El diseño experimental encuentra aplicaciones en la industria, la agricultura, la mercadotecnia, la medicina, la ecología, las ciencias de la conducta, etc. constituyendo una fase esencial en el desarrollo de un estudio experimental.
Introducción histórica
Los investigadores realizan experimentos en prácticamente todos los campos de investigación científica o técnica, con la finalidad de descubrir algo sobre un proceso o sistema en particular. Literalmente, un experimento es una prueba o más foralmente, un conjunto de pruebas en las que se realizan cambios intencionados en las variables de entrada (factores) de un proceso o sistema para poder observar e identificar las razones de los cambios que puedan observarse en la respuesta de salida (respuesta experimental). Cualquiera de estos experimentos requieren de una planificación previa y dependiendo de cómo se realice esta, el resultado final puede variar en gran medida. Un experimento con un buen diseño y un modelo adecuado no solo proporciona más información, sino que también permite lograr condiciones experimentales óptimas, mientras que un experimento con un diseño fallido puede proporcionar información muy deficiente.[2]
En sentido amplio, un diseño experimental no es más que un plan para descubrir o probar conexiones causales, siendo el experimento la ejecución de dicho plan. En un sentido más restringido, el diseño experimental incluye la idea de que el investigador provoca un fenómeno en lugar de esperar a que ocurra. Por consiguiente, es posible conjeturar que ya el hombre primitivo realizaba experimentos sobre la base de un plan. Ello le permitió, por ejemplo, diferenciar las plantas medicinales de las venenosas, establecer el método más efectivo para cazar animales o introducir mejoras en sus herramientas.[3] Sin embargo, estos experimentos, en su mayoría, no se basaban en un estudio sistemático de las condiciones experimentales, como establece el principio del diseño experimental, sino, más bien en ensayos de prueba y error en los que rara vez se modificaba más de una variable. Este tipo de pruebas basadas en ensayo y error no suelen ser muy eficaces, aunque no quiere ello decir que no puedan terminar en importantes mejoras tecnológicas o del conocimiento, pues de hecho se han venido utilizado desde los albores de la humanidad con mayor o menor éxito. Lo que ocurre es que a menudo redundan en un consumo de tiempo y de inversión económica alto, pues no siempre las mejoras entre dos pruebas son apreciables, pudiendo darse el caso de que en algunas ocasiones los resultados de verificación sean incluso peor, lo que obliga al experimentador a volver hacia atrás y en casos extremos a replantear nuevamente el proceso de optimización. Es a partir del Renacimiento cuando comienzan a sentarse las bases lógicas de lo que luego será el razonamiento experimental, apareciendo las primeras sistematizaciones relevantes sobre procedimientos experimentales; es decir, con la aparición del método científico.
El empleo de la metodología estadística en la experimentación científica y técnica empezó a utilizarse en el siglo XIX, siendo el filósofo-científico Charles S. Peirce quien desarrolló una teoría de la inferencia estadística en "Ilustraciones de la lógica de la ciencia" (1877-1878) y "Teoría de la inferencia probable" (1883), dos publicaciones que enfatizaron la importancia de la inferencia basada en la aleatorización en estadística.[4] Peirce también realizó diseños ciegos de medidas repetidas para evaluar su capacidad para discriminar pesos. Este experimento de Peirce inspiró a otros investigadores en psicología y educación, quienes desarrollaron una tradición de investigación de experimentos aleatorios en laboratorios y libros de texto especializados en el siglo XIX.[5] Durante el siglo XIX y comienzos del siglo XX se sentaron las bases de las herramientas estadísticas para el diseño y optimización de los experimentos. Joseph Diaz Gergonne sugirió un diseño pionero para la optimización mediante modelos de regresión polinómica en 1815 y el mismo Peirce también contribuyó con la primera publicación sobre un diseño óptimo para modelos de regresión en 1876. [6] Ya, en el siglo XX, en 1918, la matemática danesa Kirstine Smith publicó diseños de optimización mediante modelos polinomios de grado seis (y menores) por lo que se considera a esta científica la creadora del campo del diseño óptimo de experimentos.[7]
Sin embargo, el gran pionero del diseño experimental estadístico, visto desde un punto de vista más general, fue Ronald A. Fisher, considerado como el padre del diseño experimental. A la lista de los pioneros de su uso hay que añadir los de Frank Yates, W.G. Cochran y George Edward Box. Muchas de las aplicaciones originarias del diseño experimental estuvieron relacionadas con la agricultura y la biología, disciplinas de las que procede parte de la terminología propia de dicha técnica. Las aplicaciones a la industria textil comenzaron en la década de 1930 en Inglaterra y se popularizaron y extendieron a las industrias química y manufacturera de Europa y EE. UU. tras la II Guerra Mundial. Es de notar su uso actual en la industria de la electrónica y los semiconductores.
Fisher
Durante la década de 1920 y comienzo de la de 1930, el biólogo y estadístico inglés Ronald Fisher fue el responsable del análisis de datos y estudio estadístico de la Rothamsted Agricultural Experimental Station, en las proximidades de Londres y mediante el estudio de los datos obtenidos, se percató de que ciertas fallas en la forma en que se había realizado el experimento, generaban resultados que a menudo dificultaban su posterior evaluación y análisis. Interactuando con científicos e investigadores de diversos campos, desarrolló las ideas que condujeron a los principios básicos del diseño experimental: aleatorización, replicación y manejo en bloques. Fischer introdujo sistemáticamente el pensamiento estadístico y los principios de la investigación experimental, incluyendo el concepto de diseño factorial y el análisis de varianza. Sus libros The Arrangement of Field Experiments (1926) y The Design of Experiments (1935), publicados en sucesivas ediciones durante gran parte del siglo XX, tuvieron una profunda influencia en el uso de la estadística en la experimentación científica.[8]
Principios de Fisher
Buena parte de su obra pionera trató de las aplicaciones agrícolas de sus métodos de estadística. Por ejemplo, describió cómo probar la hipótesis de la catadora de té. Estos métodos estadísticos se han adaptado tanto a las ciencias experimentales como a las ciencias sociales y se usan todavía, de forma amplia y profusa en múltiples campos de la ingeniería y de la industria que se difieren del diseño y análisis de experimentos de computación.
- Comparación
- En algunos campos de estudio no es posible tener medidas independientes que conectan a una norma de metrología trazable. Comparaciones entre tratamientos se valen mucho más y normalmente se las prefieran. A menudo se compara con un control científico o tratamiento tradicional que actúa como un punto de referencia.
- Aleatorización
- Aleatorización es el proceso de asignar individuos al azar a grupos o a grupos distintos en un experimento. La asignación aleatoria a grupos (o condiciones adentro de un grupo) distingue a rigorosos verdaderos experimentos de un estudio observacional o cuasi-experimental.[9] Existe un cuerpo extensivo de teoría matemática que explora las consecuencias de asignar las unidades de tratamiento por medio de algún método aleatorio como las tablas de números aleatorios, o el uso de aparatos aleatorios como naipes o dados. Asignar unidades de tratamiento aleatoriamente tiende a mitigar los factor de confusión, los cuales hacen que los efectos que no son por tratamientos parecer como sí fuesen resultados del tratamiento. Los riesgos que se asocian con una asignación aleatoria (como tener un desbalance serio en una característica clave entre un grupo en tratamiento y un grupo de control) se calculan y así se las dirigen a un nivel más bajo y aceptable por el hecho de usar bastantes unidades de experimentación. Se pueden generalizar los resultados de un experimento de las unidades de experimentación a una población estadística de unidades pero solo si las unidades de experimentación son un muestreo de la población más grande; el error probable de tal extrapolación depende del tamaño de la muestra, entre otras cosas.
- Réplica estadística
- Normalmente se sujetan medidas a la variación y la incertidumbre de medidas significa que se las repiten y con experimentos enteros se los replican para ayudar a identificar los fuentes de la variación, por poder estimar los efectos verdaderos de tratamientos, por fortalecer su fiabilidad y su validez, y por agregar al conocimiento del tópico.[10] Sin embargo, necesita el cumplimiento de ciertas condiciones antes que la réplica se comience: la cuestión de investigación original se ha publicado en una revista de revisión por pares o citado ampliamente, el investigador es independiente del experimento original, el investigador debe primero intentar replicar los resultados del experimento original usando la data original, y el resumen debe decir que el estudio es una réplica que intente seguir en los pasos del original en lo más estricto posible.[11]
Prueba F de Fisher
Se utiliza para las comparaciones de los componentes de la desviación total. Por ejemplo, en una forma, o el ensayo ANOVA de un solo factor, la significación estadística es probada para comparando la estadística de la prueba de F
donde:
- Número de tratamientos: , I
- Total de casos: , nT'
a F-distribución con el del I-1, secundario< del > n< T> /sub grados de libertad. Usar la F-distribución es un candidato natural porque la estadística de la prueba es el cociente de dos sumas malas de los cuadrados que tienen a distribución del chi-cuadrado.
Principios básicos y pautas en el diseño experimental
El diseño experimental suele tener, como fin último, el establecimiento de los valores que deben tomar aquellos factores que afectan al resultado experimental, de forma que en el futuro se obtengan los resultados óptimos (p. e. máximo rendimiento de la producción, menor costo, etc.) cuando se apliquen esos valores. Para alcanzar este fin, en primer lugar se deben seleccionar aquellos factores más importantes que tienen el mayor efecto sobre el resultado final buscado y basándose en la experiencia subjetiva del experimentador hacer ensayos independientes para determinar sus valores óptimos. El éxito dependerá del nivel de conocimiento del experto en la materia. Si el conocimiento es bajo, la carga de trabajo podría ser considerable. Un segundo enfoque en este proceso de optimización, es el tratamiento sistemático, tanto en la investigación de los factores, como en su optimización.[12] Para realizar un experimento de manera más eficiente, se debe emplear un enfoque científico basado en criterios que eviten la subjetividad del experimentador, para lo cual se requiere un enfoque estadístico en la planificación de los experimentos (diseño experimental) para, así, poder llegar a conclusiones válidas y objetivas.
El enfoque estadístico en el diseño y análisis de un experimento, es necesario para que todos los involucrados en el experimento tengan una idea clara de exactamente qué se va a estudiar, cómo se van a recolectar los datos y al menos una comprensión cualitativa de cómo se van a analizar estos datos. Las optimizaciones sistemáticas se llevan a cabo de acuerdo con la siguiente secuencia general:[13]
- Reconocimiento y planteamiento del problema. Es el primer paso, y el más obvio. Es preciso tener una idea clara de para qué se va a plantear el diseño experimental y qué es lo que se quiere conseguir con él. A menudo se busca buscar las condiciones de trabajo para conseguir una señal instrumental más intensa o la menos interferida, en un proceso industrial, obtener el producto en el menor tiempo posible, el menor coste, etc.
- Elección de los factores, niveles e intervalo. En este segundo paso es necesario establecer e identificar qué variables o factores afectan al resultado buscado. Al considerar los factores que pueden influir en el rendimiento de un proceso o sistema, el experimentador suele descubrir que estos factores pueden clasificarse como factores de diseño potenciales y en factores de interferencia. Cuando el número de factores o variables es reducido, pueden incluirse todos en el diseño experimental, pero si el número de estos es elevado, es preciso hacer una selección de aquellos factores que tienen mayor efecto sobre el resultado experimental y con ellos realizar el diseño. Una vez establecidos los factores que se incluirán en el estudio, es necesario establecer el intervalo de variabilidad de dichos factores y sus niveles de variación. El diseño puede ser para dos niveles de variación (el valor máximo y el mínimo del intervalo) o incluir uno más niveles intermedios. Hay que tener en cuenta que cuanto mayor sea el número de factores a considerar y mayor el número de niveles de variación de estos, más complejo y amplio será el diseño resultante, lo que, desde el punto de vista estadístico hace que el diseño sea más fiable, pero por otro lado dispara el costo económico y el tiempo necesario para ejecutar el diseño en su totalidad. En algunos casos el objetivo del experimento simplemente es la detección de factores con mayor influencia o la caracterización de procesos. En estos casos, generalmente es mejor mantener bajo el número de niveles de factores.
- Selección de la variable de respuesta. Es decir, que es lo qué se va a medir tras el experimento o cómo se va a hacer su seguimiento. Esta variable de respuesta puede ser una medida realizada con un instrumento y que tenga algún tipo de relación directa con el resultado del experimento. Por ejemplo, en un estudio estructural, puede ser la resistencia a la deformación del objeto que se va a fabricar o del material que se va a utilizar. La variable seleccionada como respuesta experimental debe ser aquella que realmente provea información útil sobre el proceso bajo estudio. En estudios en los que se busca la estabilidad del resultado en el tiempo (p.ej. estudios sobre el deterioro de materiales) la variable de respuesta puede ser los valores de la media de las réplicas realizadas a intervalos de tiempo determinados o los valores de sus desviaciones estándar.[13]
- Elección del diseño experimental adecuado. Una vez decididos los factores, el intervalo y niveles de los factores y la variable de respuesta, el siguiente paso es realizar el diseño experimental en sí. La elección del diseño implica consideraciones relacionadas con el tamaño de la muestra (número de réplicas), la selección de un orden de ejecución adecuado para el ensayo experimental y la decisión de si se incluye algún tipo de restricción en el empleo de bloques o en la aleatorización.
- Ejecución de los experimentos. Una vez hecho el diseño, es necesario ejecutar los experimentos y hacer las mediciones oportunas. Al realizar el experimento, es muy importante supervisar cuidadosamente el proceso para garantizar que todo se realice según lo previsto, ya que es fácil subestimar los aspectos logísticos y de planificación de la ejecución en un entorno complejo de fabricación o investigación y desarrollo. Coleman y Montgomery sugieren que, antes de realizar el experimento, suelen ser útiles algunas pruebas piloto.[14]
- Análisis estadísticos de los resultados. Los datos obtenidos de los diferentes experimentos incluidos en el diseño deben ser evaluados mediante procedimientos estadísticos, con el fin de que las conclusiones que se deriven de ellos sean de naturaleza objetiva, nunca crítica.
- Conclusiones y recomendaciones.
Durante todo este proceso, es importante tener en cuenta que la experimentación es una parte importante del proceso de aprendizaje, donde se formulan tentativas de hipótesis sobre un sistema, se llevan a cabo experimentos para investigar estas hipótesis y, en base a los resultados, se formulan nuevas hipótesis, y así sucesivamente, tal y como estable el método científico.
Diseño factorial
Los diseños experimentales pueden ser de un solo factor o variable o de dos o más factores tratados simultáneamente. Cuando están implicados dos o más factores en el diseño experimental (diseño multivariante o multifactorial) se suele recurrir a diseños factoriales, ya que se consideran muy eficientes para este tipo de experimentos, sobre todo al inicio de un estudio experimental, donde aún se desconocen los factores más influyentes, sus rangos de influencia y sus interacciones, y a que los diseños factoriales permiten realizar experimentos en todo el espectro de factores.[15] Este tipo de experimentos permiten el estudio del efecto de cada factor sobre la variable respuesta, así como el efecto de las interacciones entre factores sobre dicha variable.
Los experimentos factoriales se basan en la variación simultánea de todos los factores en un número limitado de niveles, por lo que el número total de experimentos que deberán llevarse a cabo con este tipo de diseño se puede establecer de antemano, ya que matemáticamente se tratan de variaciones con repetición.
Donde N indica el número total de experimentos en función de los niveles, l, elegidos y de los factores, k, incluidos en el experimento. De esta manera, en el caso de diseño factorial más sencillo, el de dos factores y dos niveles en cada factor (diseño factorial de 2×2) es necesario realizar 4 experimentos . Para tres factores y dos niveles por factor, el número de experimentos será igual a 8 (23) o si fuera para igual número de factores pero tres niveles, la cantidad total de experimentos a realizar sería N=33; es decir 27 y así sucesivamente.
Notación
En los diseños experimentales en general, y en los factoriales en particular, es frecuente codificar tanto los factores, como los niveles en los que estos van a variar. Esto se hace por pura comodidad y para ahorrar espacio, sobre todo cuando los nombres de los factores son relativamente largos o complejos y los valores de los niveles, números grandes o con varios decimales, lo que dificulta su escritura. En cualquier caso, nada indica que no pueda hacerse el diseño experimental con factores y niveles sin codificar. También es habitual escalar los valores de los niveles. El escalado consiste en transformar los valores de las variables o factores de forma que estén confinados en un rango [a, b], típicamente [-1, 1]. A veces, cuando con el diseño experimental se busca encontrar qué factores tienen mayor influencia sobre la respuesta experimental, también se suele llevar a cabo una normalización. La normalización consiste en transformar los factores de forma que todos compartan un mismo valor medio y una misma desviación media.
En este sentido, un diseño experimental que fuera de dos factores para dos niveles de variabilidad de cada factor, los factores podrían codificarse, por ejemplo, como factor A y factor B o, también, factor x1 y factor x2, o de cualquier otra forma que se crea oportuna. En cuanto a los niveles, si van a ser dos y van a estar escalados, el nivel más bajo de cada factor recibe la notación -1 y el más alto +1. En este caso particular, o en otros diseños para dos niveles, para simplificar, es frecuente utilizar solo los signos - y +. De esta manera, un diseño factorial de dos factores para dos niveles consistiría en cuatro experimentos (N = 22): experimento 1; − −, experimento 2; + −, experimento 3; − +, y experimento 4; + +. También existen otras notaciones utilizadas en diseños de dos niveles, como por ejemplo, denominar el nivel más bajo con el valor 0 y el nivel mas alto con el valor 1. Otra notación, cuando los factores se han codificado con letras mayúsculas, es indicar con la misma letra que el factor, pero en minúscula, el experimento del diseño en que dicho factor se encuentra en el nivel máximo, dando por hecho que el otro se encuentra en su nivel mínimo. Cuando ambos factores se encuentran en el nivel máximo, el experimento se indica con ambas letras y cuando coincide con la combinación en que todos los factores se encuentran en el nivel mínimo, el experimento se codifica con 1.[16] La siguiente tabla muestra diferentes notaciones para un diseño N = 22.
| Experimento | Factor | Combinación | Factor | ||
|---|---|---|---|---|---|
| A (x1) | B (x2) | A (x1) | B (x2) | ||
| 1 | - | - | 1 | 0 | 0 |
| 2 | + | - | a | 1 | 0 |
| 3 | - | + | b | 0 | 1 |
| 4 | + | + | ab | 1 | 1 |
Para mantener el principio de Fisher, de que los experimentos deben de ser replicados y aleatorizados para una mayor garantía estadística de los resultados finales, es muy recomendable que estos experimentos se repitan varias veces y siempre se ejecuten de forma aleatoria, no necesariamente en el orden del diseño, ya que de esta manera se minimizan ciertos errores sistemáticos debidos a variaciones incontroladas por el experimentador.[17]
Diseño factorial completo
Los diseños factoriales también pueden hacerse para un mayor número de factores o para un mayor número de niveles o ambas cosas a la vez. En la siguiente tabla se muestra como sería un diseño factorial para dos factores y tres niveles. En este caso, el número de experimentos (sin réplicas) sería N = 32; es decir nueve experimentos. Los factores y los niveles se muestran tanto codificados como no codificados, para una mejor apreciación de las relación entre ambos. Corresponde a un supuesto experimento en el que se buscan las condiciones óptimas para obtener el mejor rendimiento en una reacción química que depende, principalmente, del pH del medio y de la temperatura. Para realizar el diseño, una vez que se ha decidido que estos son los factores, el siguiente paso es establecer el intervalo de variabilidad de cada factor. Pongamos por caso, que debido a los conocimientos previos de que se dispone, el intervalo de pH puede variar entre 3 y 9 y el de la temperatura entre 10 y 40 °C. Como el diseño va a ser para tres niveles, se escogerá el nivel más bajo, el más alto y el intermedio de cada factor. En el diseño codificado estos serán [-1,0,1], que corresponderán a los valores de los factores 3, 6 y 9, para el pH y 10, 25 y 40 °C para la temperatura. Una vez que se han tomado estas decisiones, el siguiente paso es realizar tantos experimentos como posibles combinaciones puedan hacerse entre los factores y los niveles.
| Experimento | Factor (codificado) | Factor (no codificado) | |||
|---|---|---|---|---|---|
| x | y | pH | Temp. (°C) | ||
| 1 | 1 | 1 | 9 | 40 | |
| 2 | 1 | 0 | 9 | 25 | |
| 3 | 1 | -1 | 9 | 10 | |
| 4 | 0 | 1 | 6 | 40 | |
| 5 | 0 | 0 | 6 | 25 | |
| 6 | 0 | -1 | 6 | 10 | |
| 7 | -1 | 1 | 3 | 40 | |
| 8 | -1 | 0 | 3 | 25 | |
| 9 | -1 | -1 | 3 | 10 | |
De igual manera, siguiendo el mismo procedimiento se pueden hacer diseños factoriales para más niveles y/o para más factores. Estos diseños factoriales reciben el nombre de diseños factoriales completos y entre sus principales ventajas, están la de permitir realizar experimentos en todo el intervalo de factores de forma equilibra, ya que como se muestran en los ejemplos anteriores, el diseño presenta cierta simetría en las experimentos diseñados, esta simetría redunda en una simplificación a la hora de evaluar los datos obtenidos de dichos experimentos.[12]
Representación gráfica de los diseños 2k
Los diseños de dos niveles pueden ser representados gráficamente. Esto permite visualizar rápidamente el diseño y suele ser útil a la hora de la interpretación de las respuestas. Si el diseño es para dos factores, la gráfica resultante es un cuadrado que se obtiene a partir de un sistema binario de coordenadas cartesianas en las que cada eje representa un factor. En estos casos es frecuente, aunque no siempre, codificar los factores como x1 y x2 y cada experimento se representa por sus correspondientes coordenadas, que para facilitar su representación se suelen utilizar los niveles escalados y centrados.
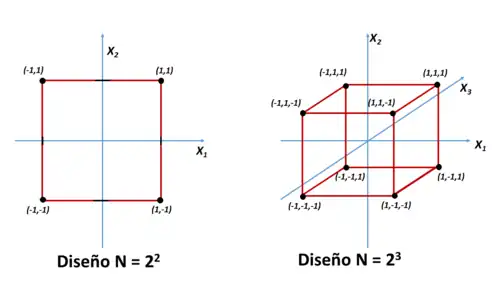
De igual manera se procede para los diseños factoriales de tres factores y dos niveles (diseño 23), en cuyo caso el gráfico será un cubo, cuyos vértices representan los ocho experimentos. Cuando el diseño está dirigido al estudio de las respuestas experimentales, los resultados de las medidas correspondientes a cada experimento se colocan junto a cada vértice, de forma que de una sola mirada se puede apreciar el resultado que tiene cada combinación de niveles y factores sobre el resultado de los experimentos.
También se han sugerido representaciones para más de tres factores. Cuando hay cuatro factores, la representación de los dieciséis experimentos (N = 24) se puede hacer con dos cubos; un cubo puede representar el cuarto factor en su nivel inferior y el otro cubo cubo puede representar el cuarto factor en su nivel superior. El número de cubos se puede duplicar para cada factor, pero este enfoque es menos útil con un mayor número de factores porque se vuelve cada vez más difícil prever los efectos.[16]
En los casos de los diseños de más de dos niveles, también es posible representarlos gráficamente, aunque a medida que aumenta el número de niveles la representación gráfica se hace más compleja. El diseño gráfico para dos factores y tres niveles (N = 32), los nueve posibles experimentos se obtendrían a partir de las coordenadas de los vértices, como en el diseño 2x2, a las que hay que añadir las cuatro coordenadas correspondientes al centro de cada lado del cuadrado mas las coordenadas del centro de la figura geométrica. En el caso de un diseño para tres factores y tres niveles, a las coordenadas de los vértices del cubo (8) hay que añadir las correspondientes a los centros de cada arista (12), las de los centros de cada cara (6) y las coordenadas del centro del cubo, en total, veintisiete experimentos (N = 33), que también se muestran en la tabla.
| Experimento
(coordenadas) |
Factor (codificado) | Experimento
(coordenadas) |
Factor (codificado) | |||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x1 | x2 | x3 | |||
| 1 | 1 | 1 | 1 | 15 | 0 | 0 | -1 | |
| 2 | 1 | 1 | 0 | 16 | 0 | -1 | 1 | |
| 3 | 1 | 1 | -1 | 17 | 0 | -1 | 0 | |
| 4 | 1 | 0 | 1 | 18 | 0 | -1 | -1 | |
| 5 | 1 | 0 | 0 | 19 | -1 | 1 | 1 | |
| 6 | 1 | 0 | -1 | 20 | -1 | 1 | 0 | |
| 7 | 1 | -1 | 1 | 21 | -1 | 1 | -1 | |
| 8 | 1 | -1 | 0 | 22 | -1 | 0 | 1 | |
| 9 | 1 | -1 | -1 | 23 | -1 | 0 | 0 | |
| 10 | 0 | 1 | 1 | 24 | -1 | 0 | -1 | |
| 11 | 0 | 1 | 0 | 25 | -1 | -1 | 1 | |
| 12 | 0 | 1 | -1 | 26 | -1 | -1 | 0 | |
| 13 | 0 | 0 | 1 | 27 | -1 | -1 | -1 | |
| 14 | 0 | 0 | 0 | |||||
Los experimentos que contienen todos los valores distintos de cero corresponden a las coordenadas de los vértices del cubo; los que contienen un cero, a las aristas; los que contienen dos ceros a los centros de las caras y el experimento de los tres ceros, corresponde a las coordenadas del centro del cubo, ya que este coincide con el origen de coordenadas.
Diseño factorial fraccionado
Siempre que el número de factores sea pequeño, los diseños factoriales completos pueden ejecutarse fácilmente. Sin embargo, con un número mayor de factores, el número de experimentos aumentará drásticamente. Así, para realizar factorial en el que se consideran 4 niveles y 3 factores, se requieren llevar a cabo N = 43 = 64 experimentos; para 4 factores y 4 niveles, N = 44 =256 y para un diseño factorial de 10 factores, aunque solo se haga para dos niveles, el número de experimentos necesarios ya se eleva a 1024 experimentos, lo cual puede resultar impracticable. Esta es una de las principales debilidades de los diseños factoriales completos. Por otro lado, una cantidad tan grande de experimentos no siempre proporciona información adicional útil o interesante; por lo tanto, realizarlos todos supone una pérdida de tiempo y recursos.[18] Existen diferentes procedimientos para reducir el número de experimentos. Uno de los más sencillos consiste en realizar solamente algunos experimentos, en número tal que sean representativos del total del diseño factorial para lo cual se han desarrollado reglas para generar un subconjunto correcto de los experimentos originales. Es lo que se conoce como diseño factorial fraccionado.
.png)
Para entender la mecánica de como se lleva a cabo el fraccionado del diseño, considérese un diseño sencillo de tres factores y dos niveles, es decir un diseño factorial N = 23 = 8 experimentos. Ahora es muy importante que los niveles estén codificados y escalados de forma simétrica, es decir, que necesariamente al nivel más alto de cada uno de los factores se codifique como 1 y al más bajo -1. Si se multiplica la columna correspondiente al factor x1 por la del factor x2 se obtiene una columna denominada producto de cruce o interacción x1•x2 (o también, fusión x1•x2). Observando atentamente esta columna, rápidamente se puede apreciar que en algunos casos este producto de cruce se corresponde con los niveles diseñados para x3. Si de este diseño factorial completo se extraen aquellos experimentos en que se da esta situación, se obtiene un nuevo diseño formado por cuatro experimentos, es decir la mitad de los iniciales.[18] Se trata ahora de un diseño factorial fraccionado N= 2k-p. En el caso de dos niveles con p = 1, la reducción del número de experimentos es la mitad. Son los llamados diseños factoriales de media fracción (1/2).
.png)
Siguiendo este procedimiento se pueden hacer fraccionamientos de cualquier diseño factorial completo para dos niveles, independientemente del número de factores que intervengan en el diseños. La columna de interacción o cruce se hace, como en el caso anterior, multiplicando las columnas de los n-1 factores y comparándola con la columna correspondiente al factor no implicado en la interacción. En todos los casos se consigue reducir a la mitad en número de experimentos del diseño completo.
Si se observa atentamente los dos diseños, el factorial completo y el fraccionado de cualquiera de las dos figuras anteriores, la correspondiente al diseño N = 23 y el correspondiente al diseño N = 24 , se aprecia en cada uno de ellos ciertas similitudes entre el diseño completo y el fraccionado:
- En ambos diseños la mitad de los experimentos comienzan por el nivel 1 y otra mitad por el nivel -1.
- En ambos diseños, para cada factor hay igual número de experimentos en el nivel 1 que en el nivel -1.
- Si observa, por ejemplo en el diseño N = 24 , la secuencia en que aparecen los niveles para el factor x2 en el diseño completo (1,1,1,1, -1,-1,-1,-1,...) es la misma que para el factor x1 en el diseño fraccionado. Lo mismo ocurre entre el factor x3 en diseño completo (1,1,-1,-1,...) respecto del x2 en el fraccionado y entre el factor x4 en diseño completo respecto del x3, en el fraccionado. Secuencias similares se pueden encontrar en otros diseños con un número diferentes de factores.
En cualquier caso, hay que tener en cuenta que a medida que se reduce el número de experimentos, la cantidad de información que puede ser obtenida a partir de ellos, también se ve reducida. Sin embargo, hay que tener en cuenta que no todas las interacciones serán significativas y que el propósito de los diseños experimentales a dos niveles suele ser simplemente determinar qué factores principales deben estudiarse en detalle posteriormente.[19] En general, este enfoque es muy popular en muchas situaciones exploratorias y tiene la ventaja adicional de que los datos son fáciles de analizar.
Otros diseños experimentales
Además de los diseños factoriales, completo o fraccionado, existen otros diseños experimentales de diferente utilidad y adaptados a las determinadas circunstancias que pueden presentarse durante el proceso experimental. Dentro de los diseños experimentales para dos niveles, N = 2k, si el número de factores es muy grande, se pueden construir diseños más pequeños, de forma que queden diseños factoriales fraccionados en los que solo se llevan a cabo 1/4 de los experimentos, N = 2k-2 o restricciones mayores, como diseños N = 2k-3 (1/8) o incluso otros fraccionamientos. Sin embargo, para conseguir estos fraccionamientos es necesario fusionar varias columnas de factores en el diseño completo y, como ya se ha indicado, hay que tener en cuenta que a medida que se reduce el número de experimentos, la cantidad de información que puede ser obtenida a partir de ellos, también se ve reducida. Por consiguiente, la introducción de estas limitaciones en el número de experimentos puede llegar a ser bastante restrictiva.
Diseños de Plackett–Burman y Taguchi
El el diseño experimental se sigue el criterio general de que el número de experimentos siempre debe ser superior al número de factores implicados. Esto quiere decir que para siete factores y dos niveles ( N = 210 = 1024), el máximo fraccionamiento que se puede hacer es N = 210-6 = 16 experimentos, ya que el siguiente fraccionamiento; N = 210-7 = 8, implica menos experimentos que factores. A medida que aumenta el número de factores, la situación se hace más compleja, de forma que se requieren 32 experimentos para el estudio de 19 factores y 64 experimentos para el estudio de 43 factores. Para superar este problema y reducir, todavía más, el número de experimentos, se necesitan otros enfoques. En este sentido, Plackett y Burman publicaron un artículo en 1946, surgido de la necesidad de realizar pruebas de componentes en la fabricación de equipos durante la Segunda Guerra Mundial y actualmente considerado como un clásico del diseño experimental.[20] Estos autores propusieron varios diseños basados en diseños factoriales de dos niveles, donde el número de experimentos es múltiplo de 4. Siguiendo unas determinadas reglas se pueden conseguir diseños en los que el número de experimentos supera en 1 al número de factores, k, lo que implica que las reducciones Plackett-Burman (diseños PB) pueden hacerse para experimentos en los que están implicados 3, 7, 11, 15, 19, 23 etc., siempre un número de factores igual a cada múltiplo de cuatro menos uno. Para evitar esta limitación de que los factores implicados en el diseño sea un múltiplo de 4 menos 1, se pueden añadir factores ficticios hasta cumplir este requisito. Dichos factores ficticios no tienen ningún efecto sobre el resultado del experimento. Así por ejemplo, si los factores implicados fueran 10, se utilizaría un diseño para 11 factores; es decir un diseño de 12 experimentos, lo que no contraviene la regla de que son necesario más experimentos que factores.[21] En la siguiente tabla se muestra, a título de ejemplo, el diseño de Plackett-Burman para siete factores:
| Experimento | Factores | ||||||
|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| 1 | - | - | - | - | - | - | - |
| 2 | + | + | + | - | + | - | - |
| 3 | - | + | + | + | - | + | - |
| 4 | - | - | + | + | + | - | + |
| 5 | + | - | - | + | + | + | - |
| 6 | - | + | - | - | + | + | + |
| 7 | + | - | + | - | - | + | + |
| 8 | + | + | - | + | - | - | + |
Un enfoque alternativo proviene del trabajo de Genichi Taguchi.[22] Taguchi establece que la calidad de un producto debe ser medida en términos de reducir al mínimo las pérdidas que ese producto causa a la sociedad, desde que inicia su fabricación hasta que concluye su ciclo de vida. Estas pérdidas sociales se traducen en pérdidas de la empresa en el medio y largo plazo. Su método de control de calidad fue ampliamente utilizado por la industria japonesa, a la vez que criticado por expertos estadísticos de occidente y solo recientemente se ha reconocido que ciertos aspectos de la teoría son muy similares a las prácticas occidentales. Sus diseños se presentan en forma de tabla, similar a la de Plackett y Burman, pero codificando con "1" el nivel inferior y con "2" el nivel alto. Aunque aparentemente los diseños de Taguchi parecen diferentes, al cambiar la notación e intercambiar filas y columnas, se aprecia el parecido entre los propuestos por Plackett y Burman, incluso los diseños más simples son iguales a los conocidos diseños factoriales fraccionales.[21]
Diseños experimentales para el ajuste de superficies de respuesta
Los diseños de dos niveles son útiles para fines exploratorios y, en ocasiones, pueden generar modelos bastante útiles. Sin embargo, en muchos aspectos de la ciencia y la tecnología, como el calibrado de instrumentos o el estudio de mezclas y proporciones, es deseable contar con varios niveles por factor.
En los procesos de calibración instrumental, habitualmente se busca ajustar la respuesta del instrumento de medida con la ayuda de una serie de patrones de referencia. A partir del calibrado se obtiene importante información técnica que permite saber si el instrumento mide correctamente o, también, poder correlacionar la medida instrumental con las variables independientes (factores), aspecto este, muy habitual en el análisis químico instrumental, donde se utilizan los calibrados para, posteriormente, generar predicciones. Para describir cuantitativamente la relación entre las respuestas y los factores, se utilizan modelos mecanicistas (fisicoquímicos) o empíricos, habitualmente modelos polinómicos, también conocidos como superficies de respuesta experimental. Estos modelos matemáticos deberían ser capaces de describir superficies de respuesta lineal y curva, de forma similar.
Para obtener los modelos de calibración más efectivos, la naturaleza del conjunto de medidas realizadas con los patrones debe considerarse cuidadosamente mediante un diseño experimental racional y dado que la relación entre factores y respuesta experimental no tienen por qué ser necesariamente lineal, es muy recomendable el empleo de tres o más factores en el diseño del calibrado. Por tanto, los diseños factoriales de tres niveles o más niveles también se conocen como diseños de superficie de respuesta. Los diseños factoriales completos de tres o más niveles pueden formalizarse de la misma manera que los diseños de dos niveles; es decir, variando los niveles y los factores hasta obtener todas las combinaciones posibles. Si el número de niveles o factores (o ambos) es elevado surge el mismo problema que con los diseños de dos niveles: el número de experimentos también se vuelve muy elevado. Estas desventajas llevaron al desarrollo de los llamados diseños óptimos en los que se incluyen niveles adicionales y experimentos centrados.[23]
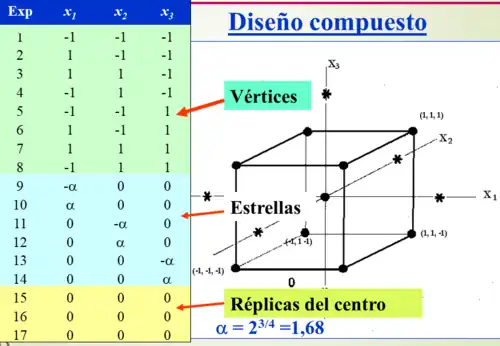
Diseño compuesto
.png)
Los diseños compuestos consisten en una combinación de un diseño factorial completo o fraccionado al que se añaden otros experimentos adicionales. Si entre los experimentos adicionales se incluye una o más réplicas de un experimento formado por el valor central que toman todos los factores, el diseño se denomina diseño compuesto central o centrado. Este tipo de diseño es el habitualmente utilizado cuando se quieren ajustar las observaciones experimentales a modelos de segundo orden,[24] ya que muestran rotabilidad o equidistancia entre experimentos, lo que les confiere una excelente robustez desde el punto de vista estadístico. Esta equidistancia se consigue mediante la inclusión de un nivel adicional, denominado nivel estrella (*) que toma un valor alfa (α) que depende del número de experimentos de la parte factorial del diseño (nF).
Como estos diseños habitualmente se utilizan para ajustar modelos matemáticos de superficies de respuesta experimental, es necesario que para una mejor estimación del error experimental, se lleven a cabo réplicas de combinaciones de factores, sobre todo del punto central, el cual se replica de tres a cinco veces asumiendo que el error es el mismo en toda la superficie de respuesta, ya que gran parte del diseño experimental se basa en la estadística clásica, donde no existe información detallada sobre las distribuciones de errores en un dominio experimental. Si existieran razones de peso para suponer que la heterocedasticidad de los errores desempeña un papel importante, la replicación debería realizarse en otros puntos (o en todos).[25]
Diseño de Box-Behnken
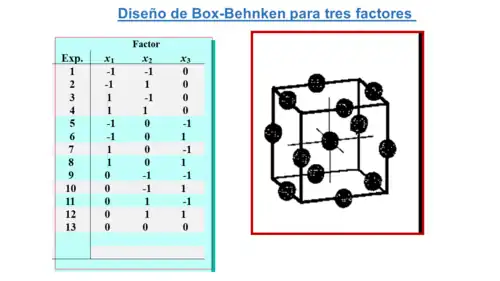
Un diseño de superficie de respuesta alternativo sería el diseño propuesto por Box y Behnken en 1960.[26] Este diseño es un diseño no factorial que incluye un experimento centrado y varios experimentos adicionales que cumplen el requisito de que, alternativamente, uno de los factores presenta un nivel central y los otros se combinan como si se tratara un díselo factorial de dos niveles. En la tabla se muestra como sería el diseño de Box-Behneken para tres factores y su representación gráfica. Cada punto del diseño corresponde a las coordenadas del centro y de las diferentes aristas del cubo, lo que supone, sin contar las réplicas del centro, 13 experimentos, muchos menos de los 27 que corresponderían a un diseño factorial completo N = 33. El diseño de Box-Behnken es, en realidad, un diseño esférico en el que todos los puntos se encuentran en la superficie de una esfera de radio .
Estos diseños permiten una estimación eficiente de los coeficientes de primer y segundo orden en modelos matemáticos de superficies de respuesta experimental. Como los diseños de Box-Behnken tienen menos puntos de diseño, pueden ser menos costosos de realizar que los diseños centrales compuestos con el mismo número de factores.[27]
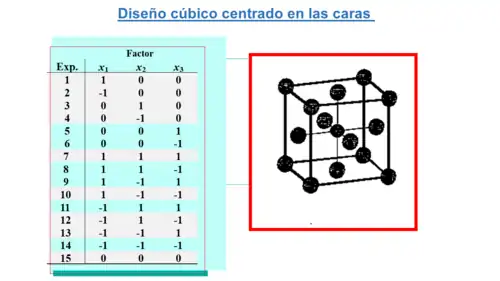
Diseño compuesto central centrado en la caras
También conocido como diseño de cubo centrado en las caras, en realidad se trata de un diseño compuesto central, en el que el valor de α es igual a 1, independientemente del número de experimentos factoriales. Este diseño coloca los puntos estrella o axiales en el centro de las caras del cubo. Esta variación del diseño compuesto central se utiliza a veces cuando sólo se requieren tres niveles de cada factor. Sin embargo, hay que tener en cuenta que carece de la propiedad de la rotabilidad. Por contra, el diseño de cubo centrado en las caras no requiere tantos puntos centrales como los modelos esféricos. En la práctica, 2 o 3 son suficientes para proporcionar una buena varianza de predicción en toda la región experimental.[24]
Diseño de optimización de mezclas
Otro diseño que tiene particular interés y muchas aplicaciones prácticas es el denominado diseño de optimización de mezclas o, simplemente, diseños de mesclas. Este tipo de diseños se utilizan en experimentos en los que los factores son los compuestos o ingredientes de una mezcla, algo muy habitual si se investigan mezclas, como pueden ser los eluyentes en cromatografía líquida o formulaciones de productos como pinturas o en la industria farmacéutica y textil y en otras situaciones por el estilo. Lo habitual es que los componentes de una mezcla se expresen en porciones de peso, volumen o moles. En estos casos, los niveles de los factores no son independientes, sino que obligatoriamente, la suma de todos ellos debe ser igual al 100% o, si están normalizados, a 1.[12] En otras palabras, si en una mezcla de tres ingredientes A, B y C hay 50% de A y 25% de B, forzosamente la proporción de C deberá ser del 25%.
Para este tipo de diseños, el procedimiento a seguir es, básicamente, el mismo que para los diseños vistos anteriormente; en primer lugar, se codifican los factores o componentes de la mezcla y seguidamente se establecen los niveles de variabilidad de cada factor. Para simplificar, la codificación de los factores se hace mediante letras y las de los niveles, con valores que van desde el 0 al 1, donde 0 representa el 0% en la mezcla y 1 el 100%. Una vez que se dispone de los factores y los niveles, el siguiente paso es realizar todas las combinaciones posibles, pero siempre con la restricción de que la suma de los niveles para cada experimento, tiene que ser 1. Así, por ejemplo, en el caso más sencillo de dos componentes, A y B y cinco niveles, 0, 0.25, 0.50, 0.75 y 1, de las 25 posibles combinaciones de factores y niveles, solo están permitidas 5:
| Exp. | Factor | |
|---|---|---|
| A | B | |
| 1 | 1 | 0 |
| 2 | 0.75 | 0.25 |
| 3 | 0.5 | 0.5 |
| 4 | 0.25 | 0.75 |
| 5 | 0 | 1 |
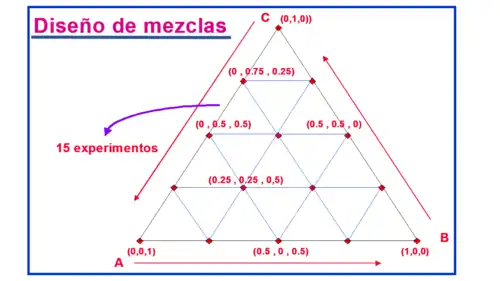
De igual manera se procede para los diseños en los que el número de componentes de la mezcla es mayor; una vez que se han decidido los niveles de los factores, del posible diseño factorial completo, se extraen aquellos experimentos que cumplen el requisito de que la suma de las proporciones es del 100%. En diseños para tres componentes, para simplificar el cálculo, se utilizan unos diagramas reticulados de forma triangular en los que cada lado representa un componente y a cada uno de dichos lados se colocan, de forma escaladas, marcas que representan cada nivel. Uniendo las diferentes marcas mediante líneas paralelas a los lados se obtiene una retícula en la que cada nodo representa un experimento de los que se puede deducir la proporción en la que debe encontrarse cada componente.
Aplicaciones
El diseño de experimentos tiene una gran variedad de aplicaciones y puede ser aplicado a un gran número de industrias, la optimización de recursos, la identificación de causas de variabilidad son algunos de los objetivos del diseño de experimentos aplicados en nivel industrial.
Aplicaciones según la clasificación de la industria
A continuación se muestran algunos ejemplos de aplicaciones existentes según el tipo de industria.
Industrias pesadas o de base
- Química pesada
- Estudio de la composición para la elaboración de productos: Estudio de los valores más apropiados para la elaboración de compuestos químicos que requieran diversos componentes. Análisis del efecto de las condiciones del entorno en la elaboración del producto como la temperatura ambiente, humedad relativa etc.[28]
Industrias de bienes de equipo
- Maquinaria
- Medida de la variabilidad de los instrumentos de medida: Es posible aplicar el diseño de experimentos como herramienta para determinar y mejorar los índices de capacidad de un proceso concreto apoyándose en estudios de reproducibilidad y repetitividad.[29]
- Diseño de motores eléctricos: Estudio de las características constructivas del motor y su influencia en variables importantes como la pérdida de flujo y la constante de velocidad.[30]
- Diseño de electrodos: Estudio de los esfuerzos en los electrodos en función de la fuerza de aplicación y el tamaño del electrodo.[31]
- Diseño de elementos de sujeción: Análisis de la influencia de los parámetros geométricos en la resistencia de los remaches.[32]
- Materiales de construcción
- Estudios de corrosión: Estudios de la influencia del tiempo en la corrosión de aceros de construcción y metales en general.
- Aplicaciones en el mecanizado: estudio de la variabilidad en los procesos de mecanizado, ayuda a la reducción de piezas defectuosas y aumento de la capacidad de producción.[33]
- Producción de vehículos industriales
- Estudio de procesos de soldadura: estudio de un proceso de soldadura, para determinar las variables que influyen en la resistencia de la soldadura.[34]
- Industria aeronáutica
- Optimización del proceso de anodizado y pintado: optimizar los procesos de anodizado y pintado para conseguir una buena protección anticorrosion.[35]
Industrias ligeras o de uso y consumo
- Farmacia y química ligera
- Informática y telecomunicaciones
- Estudio del rendimiento de una red informática: Realizando simulaciones es posible cuantificar el rendimiento y las variables críticas que hacen que la transferencia de datos en la red sea económicamente rentable.[36]
- Mejora del rendimiento de un procesador: Se usa para determinar el impacto que tienen variables importantes como la temperatura y las horas de uso en el rendimiento del procesador.
- Reducción del tiempo del CPU: El estudio se basa en la aplicación del diseño de experimentos para determinar la mejor combinación de factores que reduzcan el tiempo de CPU.
- Optimización de materiales en semiconductores: Estudio de las propiedades eléctricas del arsienuro de galio dopado con silano.[37]
- Diseño de filtros pasivos: se utiliza el diseño de experimentos para determinar los valores de las tolerancias de los componentes para optimizar los circuitos.[38]
- Biotecnología
- Operaciones en un sistema de fangos activos: optimizar y entender las reacciones que se dan en el tratamiento secundario de una EDAR, por ejemplo, los fangos activos.[39]
Un ejemplo
Un ingeniero quiere estudiar la resistencia de una pieza plástica sometida a temperaturas cambiantes. La pieza puede ser elaborada con tres tipos de plástico distintos. De ahí que se plantee las siguientes preguntas:
- ¿Qué efecto tienen la composición de la pieza y la temperatura en la resistencia de la pieza?
- ¿Existe algún material con el que la pieza resulte más resistente que con cualquiera de los otros dos independientemente de la temperatura?
Para darles respuesta, el ingeniero se plantea realizar una batería de experimentos. Cada uno de ellos consiste en tomar una pieza de un material dado, someterla a una temperatura prefijada y aplicarle una presión hasta que la pieza se quiebre. El grado de presión necesario será la medida de resistencia de la pieza.
Por fijar ideas, selecciona tres temperaturas, -20 °C, 20 °C y 60 °C. Por lo tanto, puede realizar 9, es decir, 3x3, pruebas distintas. Además, decide repetir cada una de las 9 pruebas 4 veces cada una. Finalmente, decide aleatorizar las pruebas, es decir, desordenarlas aleatoriamente en el tiempo.
Tras realizar los experimentos, obtiene 36, es decir, 4x9, medidas de resistencia distintas. A partir de ese momento, realiza un estudio cuantitativo utilizando técnicas estadísticas, como la ANOVA, que ya no forman parte propiamente de la fase del diseño experimental.
Véase también
- Ciencia
- Método científico
- Metodología
- Diseño factorial
- Contraste de hipótesis
- Diseño de experimentos
Referencias
- ↑ Montgomery, Douglas C. (2001). «Chap. 1.3. Basic principles». Design and analysis of experiments (en inglés) (5th ed edición). John Wiley. ISBN 978-0-471-31649-7.
- ↑ Liang, Yi-zeng; Fang, Kai-tai; Xu, Qing-song (28 de septiembre de 2001). «Uniform design and its applications in chemistry and chemical engineering». Chemometrics and Intelligent Laboratory Systems 58 (1): 43-57. ISSN 0169-7439. doi:10.1016/S0169-7439(01)00139-3. Consultado el 1 de agosto de 2025.
- ↑ Pablo Cazau (2013). «Una reseña histórica de los diseños experimentales». Consultado el 1 de agosto de 2025.
- ↑ Stigler, Stephen M. (1 de marzo de 1978). «Mathematical Statistics in the Early States». The Annals of Statistics 6 (2). ISSN 0090-5364. doi:10.1214/aos/1176344123. Consultado el 1 de agosto de 2025.
- ↑ Dehue, Trudy (1997-12). «Deception, Efficiency, and Random Groups: Psychology and the Gradual Origination of the Random Group Design». Isis (en inglés) 88 (4): 653-673. ISSN 0021-1753. doi:10.1086/383850. Consultado el 1 de agosto de 2025.
- ↑ Peirce, C. S. (1967-08). «Note on the Theory of the Economy of Research». Operations Research (en inglés) 15 (4): 643-648. ISSN 0030-364X. doi:10.1287/opre.15.4.643. Consultado el 1 de agosto de 2025.
- ↑ Smith, K. (1 de noviembre de 1918). «ON THE STANDARD DEVIATIONS OF ADJUSTED AND INTERPOLATED VALUES OF AN OBSERVED POLYNOMIAL FUNCTION AND ITS CONSTANTS AND THE GUIDANCE THEY GIVE TOWARDS A PROPER CHOICE OF THE DISTRIBUTION OF OBSERVATIONS». Biometrika (en inglés) 12 (1-2): 1-85. ISSN 0006-3444. doi:10.1093/biomet/12.1-2.1. Consultado el 1 de agosto de 2025.
- ↑ Montgomery, Douglas C. (2001). «Chap. 1-5. A brief history of statistical design». Design and analysis of experiments (en inglés) (5. ed edición). Wiley. ISBN 978-0-471-31649-7.
- ↑ Creswell, J.W. (2008). Educational research: Planning, conducting, and evaluating quantitative and qualitative research (3rd). Upper Saddle River, NJ: Prentice Hall. 2008, p. 300. ISBN 0-13-613550-1
- ↑ Dr. Hani (2009). «Replication study». Archivado desde el original el 2 de junio de 2012. Consultado el 27 de octubre de 2011.
- ↑ Burman, Leonard E.; Robert W. Reed; James Alm (2010). «A call for replication studies» (journal article). Public Finance Review. pp. 787-793. doi:10.1177/1091142110385210. Archivado desde el original el 6 de mayo de 2021. Consultado el 27 de octubre de 2011.
- ↑ a b c Otto, Matthias (2017). «Chap. 4. Optimization and Experimental Design». Chemometrics: statistics and computer application in analytical chemistry (Third edition edición). Wiley-VCH Verlag GmbH & Co. KGaA. ISBN 978-3-527-34097-2.
- ↑ a b Montgomery, Douglas C. (2001). «Chap. 1-4. Guidelines for designing experiments». Design and analysis of experiments (en inglés) (5th ed edición). John Wiley. ISBN 978-0-471-31649-7.
- ↑ Coleman, David E.; Montgomery, Douglas C. (1993-02). «A Systematic Approach to Planning for a Designed Industrial Experiment». Technometrics (en inglés) 35 (1): 1-12. ISSN 0040-1706. doi:10.1080/00401706.1993.10484984. Consultado el 6 de agosto de 2025.
- ↑ Otto, Matthias (2017). «Chap. 4.3. Experimental Design and Response Surface Methods». Chemometrics: statistics and computer application in analytical chemistry (en inglés) (Third edition edición). Wiley-VCH. ISBN 978-3-527-34097-2.
- ↑ a b Morgan, Ed (1991). «Chap. 3.2. Factorial experiments at two leveles». Chemometrics: experimental design. Analytical chemistry by open learning (en inglés). J. Wiley & sons. ISBN 978-0-471-92903-1.
- ↑ Miller, J. N.; Miller, J.C. (2002). «Cap. 7.2. Aleatorización y formación de bloques». Estadística y Quimiometría para Química Analítica. Prentice Hall. ISBN 84-205-3514-1.
- ↑ a b Brereton, Richard G. (2018). «Chap. 2.3.2. Fractional Factorial Designs». Chemometrics: data driven extraction for science (en inglés) (Second edition edición). John Wiley & Sons. ISBN 978-1-118-90468-8.
- ↑ Brereton, Richard G. (2018). «Chap. 2.3.2. Fractional Factorial Designs». Chemometrics: data driven extraction for science (en inglés) (2nd ed edición). John Wiley & sons. ISBN 978-1-118-90467-1.
- ↑ Plackett, R. L.; Burman, J. P. (1946). «THE DESIGN OF OPTIMUM MULTIFACTORIAL EXPERIMENTS». Biometrika (en inglés) 33 (4): 305-325. ISSN 0006-3444. doi:10.1093/biomet/33.4.305. Consultado el 22 de agosto de 2025.
- ↑ a b Brereton, Richard G. (2018). «Chap. 2.3.3. Plackett–Burman and Taguchi Designs». Chemometrics: data driven extraction for science (en inglés) (2nd ed edición). John Wiley & sons. ISBN 978-1-118-90467-1.
- ↑ Taguchi, Genichi; Taguchi, Genichi (1988). System of experimental design: engineering methods to optimize quality and minimize costs. UNIPUB/Kraus International Publ. [u.a.] ISBN 978-0-527-91621-3.
- ↑ Otto, Matthias (2017). «Chap. 4.3. Experimental Design and Response Surface Methods». Chemometrics: statistics and computer application in analytical chemistry (en inglés) (Third edition edición). Wiley-VCH. ISBN 978-3-527-34097-2.
- ↑ a b Montgomery, Douglas C. (2001). «Chap. 11-4.2. Desigs for Fitting the Second-Order Model». Design and analysis of experiments (en inglés) (5. ed edición). Wiley. ISBN 978-0-471-31649-7.
- ↑ Brereton, Richard G. (2018). «Chap.2.4. Central Composite or Response Surface Designs». Chemometrics: data driven extraction for science (en inglés) (Second edition edición). John Wiley & Sons. ISBN 978-1-118-90468-8.
- ↑ Box, G. E. P.; Behnken, D. W. (NOVEMBER, 1960). «Some New Three Level Designs for the Study of Quantitative Variables». TECHNOMETRICS 2 (4): 455-476.
- ↑ Minitab. «¿Qué son los diseños de superficie de respuesta, los diseños centrales compuestos y los diseños de Box-Behnken?». support.minitab.com. Consultado el 25 de agosto de 2025.
- ↑ Jack E. Reece Ph.D., Honeywell. "Consider the Metric: Dealing with Mixtures and Temperature Gradients"
- ↑ Dale Owens."Reduction of Measurements Device Variability Using Experimental Design Techniques". Kurt Manufacturing Minneapolis. Minnesota
- ↑ Karen Cornwell."Linear Motor Design" Digital Equipment Corporation
- ↑ Doug Sheldon."Factorial Experiment for Botttom Electrode Stress".Ramtron Corporation
- ↑ Tom Gardner, James D. Riggs."The Effect of the CE Rivet H parameter on Head Protusion"
- ↑ Tom Tanis."A Designed Experiment to Reduce Circular Runout". Ampex Recording Systems
- ↑ Kelly Johnson."Ball Weld Experiment". Morton International
- ↑ Tom Bingham. "Optimizing the Anodizee Process and Paint Adhesion for Sheet Metal Parts". Supplier Improvement Manager. Boeing Commercial Airplanes
- ↑ Lt Col Mark Kiemele. "Computer Network Performance Analysis" Tenure Associate Professor, United States Air Force Academy
- ↑ Alan Arnholt, Steve Smith, Robert Kaliski."Design of Eperiments Silane Doping in GaAs". Statistics Seminar Project- University of Northern Colorado
- ↑ David M. Fisk."Application of DOE to an Analog Filter Design". Defense Systems & Electronics Group, Texas Instruments Inc.
- ↑ Majors James Brickell and Kenneth Knox."Environmetal Engineeing Operation of an Activated Sludge System". Department of Civil Engineering, United States Air Force Academy