Cuadrisecante

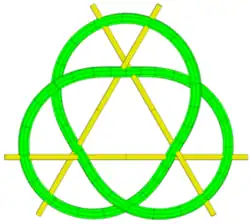
En geometría, una cuadrisecante o línea cuadrisecante de una curva espacial es una línea que pasa por cuatro puntos de la curva. Este es el mayor número posible de intersecciones que una curva espacial genérica puede tener con una línea, y para tales curvas, las cuadrisecantes forman un conjunto discreto de líneas. Las cuadrisecantes han sido estudiadas para curvas de varios tipos:

• Los nudos y enlaces en la teoría de nudos, cuando no son triviales, siempre tienen cuadrisecantes, y la existencia y número de cuadrisecantes se han estudiado en relación con invariantes de nudo, incluyendo la curvatura total mínima y la longitud de cuerda de un nudo.
• El número de cuadrisecantes de una curva algebraica no singular en el espacio proyectivo complejo puede calcularse mediante una fórmula derivada por Arthur Cayley.
• Las cuadrisecantes de disposiciones de líneas no coplanarias tocan subconjuntos de cuatro líneas de la disposición. Están asociadas con superficies regladas y la configuración del doble seis de Schläfli.

Una cuadrisecante es una línea que intersecta una curva, superficie u otro conjunto en cuatro puntos distintos. Es análoga a una línea secante, que intersecta una curva o superficie en dos puntos; y a una trisecante, que intersecta una curva o superficie en tres puntos.^[2]​

En comparación con las secantes y trisecantes, las cuadrisecantes son especialmente relevantes para las curvas espaciales, porque tienen el mayor número posible de puntos de intersección de una línea con una curva genérica. En el plano, una curva genérica puede ser cruzada arbitrariamente muchas veces por una línea; por ejemplo, pequeñas perturbaciones genéricas de la curva seno son cruzadas infinitamente por el eje horizontal. En contraste, si una curva espacial arbitraria se perturba una pequeña distancia para hacerla genérica, no habrá líneas que pasen por cinco o más puntos de la curva perturbada. Sin embargo, cualquier cuadrisecante de la curva espacial original permanecerá presente cerca de su perturbación.^[3]​ Para curvas espaciales genéricas, las cuadrisecantes forman un conjunto discreto de líneas. En cambio, cuando ocurren trisecantes, forman familias continuas de líneas.^[4]​

Una explicación para este fenómeno es visual: al observar una curva espacial desde lejos, el espacio de tales puntos de vista puede describirse como una esfera bidimensional, con un punto correspondiente a cada dirección. Los pares de hebras de la curva pueden parecer cruzarse desde todos estos puntos de vista, o desde un subconjunto bidimensional de ellos. Tres hebras formarán un cruce triple cuando el punto de vista esté en una trisecante, y cuatro hebras formarán un cruce cuádruple desde un punto de vista en una cuadrisecante. Cada restricción de que el cruce de un par de hebras esté en otra hebra reduce el número de grados de libertad en uno (para una curva genérica), por lo que los puntos de vista en trisecantes forman un subconjunto unidimensional (continuamente infinito) de la esfera, mientras que los puntos de vista en cuadrisecantes forman un subconjunto cero-dimensional (discreto). C. T. C. Wall escribe que el hecho de que las curvas espaciales genéricas sean cruzadas como máximo cuatro veces por líneas es «uno de los teoremas más simples de este tipo», un caso modelo para teoremas análogos sobre transversales de mayor dimensión.^[3]​

Dependiendo de las propiedades de la curva, puede no tener cuadrisecantes, tener un número finito o infinito de ellas. Estas consideraciones hacen que sea de interés determinar condiciones para la existencia de cuadrisecantes, o encontrar límites en su número en varios casos especiales, como curvas anudadas,^[5]​^[6]​ curvas algebraicas,^[7]​ o disposiciones de líneas.^[8]​

En el espacio euclídeo tridimensional, cada nudo o enlace manso no trivial tiene una cuadrisecante. Establecido originalmente en el caso de polígonos anudados y nudos suaves por Erika Pannwitz,^[5]​ este resultado se extendió a nudos en una posición general adecuada y enlaces con un número de enlace no nulo,^[6]​ y más tarde a todos los nudos y enlaces mansos no triviales.^[9]​

Pannwitz demostró de manera más sólida que, para un disco localmente plano que tiene el nudo como su borde, el número de singularidades del disco puede usarse para construir un límite inferior en el número de cuadrisecantes distintas. La existencia de al menos una cuadrisecante se deriva del hecho de que cualquier disco de este tipo debe tener al menos una singularidad.^[5]​^[10]​ Morton y Mond (1982) conjeturaron que el número de cuadrisecantes distintas de un nudo dado es siempre al menos ${\displaystyle n(n-1)/2}$, donde ${\displaystyle n}$ es el número de cruces del nudo.^[6]​^[10]​ Desde entonces se han descubierto contraejemplos a esta conjetura.^[10]​

Los enlaces de dos componentes tienen cuadrisecantes en las que los puntos en la cuadrisecante aparecen en orden alternado entre los dos componentes,^[6]​ y los nudos no triviales tienen cuadrisecantes en las que los cuatro puntos, ordenados cíclicamente como ${\displaystyle abcd}$ en el nudo, aparecen en el orden ${\displaystyle acbd}$ a lo largo de la cuadrisecante.^[11]​ La existencia de estas cuadrisecantes alternantes puede usarse para derivar el teorema de Fáry-Milnor, un límite inferior en la curvatura total de un nudo no trivial.^[11]​ Las cuadrisecantes también se han utilizado para encontrar límites inferiores en la longitud de cuerda de los nudos.^[12]​

G. T. Jin y H. S. Kim conjeturaron que, cuando una curva anudada ${\displaystyle K}$ tiene un número finito de cuadrisecantes, ${\displaystyle K}$ puede aproximarse con un nudo poligonal equivalente con sus vértices en los puntos donde las cuadrisecantes intersectan ${\displaystyle K}$, en el mismo orden en que aparecen en ${\displaystyle K}$. Sin embargo, su conjetura es falsa: de hecho, para cada tipo de nudo, existe una realización para la cual esta construcción lleva a un polígono que se autointersecta, y otra realización donde esta construcción produce un nudo de un tipo diferente.^[13]​

Se ha conjeturado que cada nudo salvaje tiene un número infinito de cuadrisecantes.^[9]​

Arthur Cayley derivó una fórmula para el número de cuadrisecantes de una curva algebraica en el espacio proyectivo complejo

tridimensional, como una función de su grado y género.^[7]​ Para una curva de grado ${\displaystyle d}$ y género ${\displaystyle g}$, el número de cuadrisecantes es^[14]​$${\displaystyle {\frac {(d-2)(d-3)^{2}(d-4)}{12}}-{\frac {g(d^{2}-7d+13-g)}{2}}.}$$Esta fórmula asume que la curva dada es no singular; pueden ser necesarios ajustes si tiene puntos singulares.^[15]​^[16]​

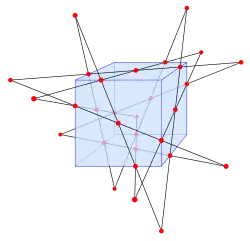
En el espacio euclídeo tridimensional, cada conjunto de cuatro líneas no coplanarias en posición general tiene ya sea dos cuadrisecantes (también llamadas en este contexto transversales) o ninguna. Cualquiera de las tres líneas determina un hiperboloide, una superficie doblemente reglada en la que uno de los dos conjuntos de líneas regladas contiene las tres líneas dadas, y la otra regladura consiste en trisecantes de las líneas dadas. Si la cuarta línea atraviesa esta superficie, tiene dos puntos de intersección, porque el hiperboloide está definido por una ecuación cuadrática. Las dos trisecantes de la superficie reglada, a través de estos dos puntos, forman dos cuadrisecantes de las cuatro líneas dadas. Por otro lado, si la cuarta línea es disjunta del hiperboloide, entonces no hay cuadrisecantes.^[17]​ En espacios con coordenadas de número complejo en lugar de coordenadas reales, cuatro líneas no coplanarias siempre tienen exactamente dos cuadrisecantes.^[8]​

Las cuadrisecantes de conjuntos de líneas juegan un papel importante en la construcción del doble seis de Schläfli, una configuración de doce líneas que se intersectan entre sí en 30 cruces. Si se dan cinco líneas ${\displaystyle a_{i}}$ (para ${\displaystyle i=1,2,3,4,5}$) en el espacio tridimensional, de modo que todas las cinco sean intersectadas por una línea común ${\displaystyle b_{6}}$ pero estén de otro modo en posición general, entonces cada una de las cinco cuádruples de las líneas ${\displaystyle a_{i}}$ tiene una segunda cuadrisecante ${\displaystyle b_{i}}$, y las cinco líneas ${\displaystyle b_{i}}$ formadas de esta manera son todas intersectadas por una línea común ${\displaystyle a_{6}}$. Estas doce líneas y los 30 puntos de intersección ${\displaystyle a_{i}b_{j}}$ forman el doble seis.^[18]​^[19]​

Una disposición de ${\displaystyle n}$ líneas complejas con un número dado de intersecciones por pares y de otro modo no coplanarias puede interpretarse como una curva algebraica con grado ${\displaystyle n}$ y con género determinado a partir de su número de intersecciones, y la fórmula mencionada de Cayley puede usarse para contar sus cuadrisecantes. El mismo resultado que esta fórmula también puede obtenerse clasificando las cuádruples de líneas por sus intersecciones, contando el número de cuadrisecantes para cada tipo de cuádruple, y sumando sobre todas las cuádruples de líneas en el conjunto dado.^[8]​