Criptografía visual

Desarrollo de máscaras que permitan superponer n transparencias A, B,... Impreso con rectángulos negros revela una imagen secreta — n = 4 requiere 16 (2 4 ) conjuntos de códigos cada uno con 8 (2 4-1 ) subpíxeles, que se pueden distribuir como 3 × 3 con el bit adicional siempre negro

La criptografía visual es una técnica de cifrado que permite codificar información visual (como imágenes, texto, etc.) de manera que la información descifrada se presente como una imagen visual.

Una de las técnicas más reconocidas fue desarrollada por Moni Naor y Adi Shamir en 1994. [1]​ Presentaron un esquema de intercambio de secretos visuales en el que una imagen binaria se divide en n partes, de manera que solo quien posea todas las n partes pueda reconstruir la imagen, mientras que cualquier conjunto de n − 1 partes no revelará información sobre la imagen original. Cada parte se imprimió en una transparencia independiente, y el proceso de descifrado se lleva a cabo al superponer las partes. Al superponer las n partes, la imagen original se revela.Hay varias generalizaciones del esquema básico, incluida la criptografía visual k de n, [2]​ [3]​ y el uso de láminas opacas pero iluminándolas con múltiples conjuntos de patrones de iluminación idénticos bajo el registro de un solo detector de un solo píxel [4]​

Siguiendo una idea similar, se pueden utilizar transparencias para implementar un cifrado de un solo uso, donde una transparencia representa una clave aleatoria compartida y la otra actúa como el texto cifrado. Normalmente, hay una expansión del requisito de espacio en la criptografía visual. Sin embargo, si una de las dos partes se organiza de forma recursiva, la eficiencia de la criptografía visual puede incrementarse hasta alcanzar el 100%. [5]​

Algunos antecedentes de la criptografía visual pueden rastrearse en patentes de la década de 1960.[6]​[7]​Otros orígenes se encuentran en estudios sobre la percepción y la comunicación segura.[8]​[9]​

La criptografía visual puede emplearse para proteger plantillas biométricas, permitiendo su descifrado sin necesidad de cálculos complejos. [10]​

Ejemplo

Una demostración de criptografía visual. Cuando se superponen dos imágenes del mismo tamaño de píxeles en blanco y negro aparentemente aleatorios, aparece el logotipo de Wikipedia .

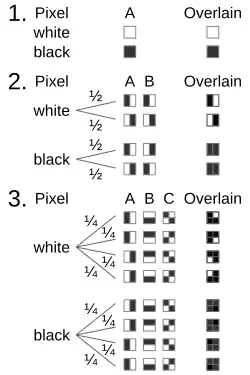
En este ejemplo, la imagen binaria se ha dividido en dos imágenes componentes. Cada una de estas imágenes contiene un par de píxeles por cada píxel de la imagen original. Estos pares de píxeles se colorean de negro o blanco según la siguiente regla:

  • Si el píxel de la imagen original es negro, los pares de píxeles en las imágenes componentes deben ser complementarios, es decir, uno debe ser ■□ y el otro □■, seleccionados de forma aleatoria. Cuando estos pares complementarios se superponen, producen un tono de gris oscuro.
  • Si el píxel de la imagen original es blanco, los pares de píxeles en las imágenes componentes deben coincidir, es decir, ambos deben ser ■□ o ambos □■. Cuando estos pares coincidentes se superponen, producen un tono de gris claro.

Cuando se superponen las dos imágenes componentes, la imagen original se revela. Sin embargo, por sí sola, una imagen componente no proporciona información sobre la imagen original; es indistinguible de un patrón aleatorio de pares ■□ / □■. Además, al contar con una imagen componente, se pueden aplicar las reglas de sombreado mencionadas anteriormente para generar una imagen componente falsa que, al combinarse con la original, produzca cualquier imagen deseada.

(2, n ) caso de intercambio de criptografía visual

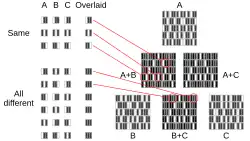
Dos transparencias cualesquiera impresas con rectángulos negros, al superponerse revelan el mensaje, aquí, una letra A (se agregaron líneas de cuadrícula para mayor claridad)

Compartir un secreto con un número arbitrario de personas, n, de modo que al menos dos de ellas sean necesarias para decodificarlo, es una variante del esquema de intercambio de secretos visuales propuesto por Moni Naor y Adi Shamir en 1994. En este esquema, una imagen secreta se codifica en n partes, que se imprimen en transparencias. Las partes parecen aleatorias y no contienen información descifrable sobre la imagen secreta subyacente; sin embargo, cuando dos de estas partes se superponen, la imagen secreta se vuelve legible para el ojo humano.

Cada píxel de la imagen secreta se representa mediante varios subpíxeles en cada imagen compartida, utilizando una matriz para definir el color de los píxeles. En el caso (2, n), un píxel blanco de la imagen secreta se codifica a través de una matriz elegida de entre el siguiente conjunto, donde cada fila corresponde al patrón de subpíxeles de uno de los componentes:

{todas las permutaciones de las columnas de} :

Por otro lado, un píxel negro en la imagen secreta se codifica utilizando una matriz seleccionada del siguiente conjunto:

{todas las permutaciones de las columnas de} :

Por ejemplo, en un esquema de compartición de secretos (2,2), donde el secreto se divide en dos partes y ambas son necesarias para su decodificación, se emplean matrices complementarias para representar un píxel negro y matrices idénticas para representar un píxel blanco. Al superponer las partes, todos los subpíxeles correspondientes a un píxel negro se tornan negros, mientras que el 50% de los subpíxeles asociados a un píxel blanco permanecen blancos.

Cómo engañar al sistema de intercambio de secretos visuales (2, n )

Horng et al. propusieron un método que permite que n − 1 partes coludidas engañen a una parte honesta en el contexto de la criptografía visual. Aprovechan el conocimiento de la distribución subyacente de los píxeles en las acciones para generar nuevas acciones que, al combinarse con las acciones existentes, forman un nuevo mensaje secreto seleccionado por los tramposos. [11]​

Sabemos que dos acciones son suficientes para decodificar la imagen secreta utilizando el sistema visual humano. No obstante, al analizar dos acciones también se obtiene información sobre la tercera acción. Por ejemplo, los participantes coludidos pueden comparar sus acciones para identificar cuándo ambos tienen píxeles negros y usar esa información para inferir que otro participante también tendrá un píxel negro en esa misma ubicación. Al conocer la ubicación de los píxeles negros en el recurso compartido de otro, pueden crear un nuevo recurso compartido que, al combinarse con el recurso compartido original, forme un nuevo mensaje secreto. De esta forma, un grupo de partes coludidas con suficientes acciones para acceder al código secreto puede engañar a las partes honestas.

Esteganografía visual

Superposición de imágenes de componentes con las letras A y B para revelar la letra S

Los subpíxeles 2×2 también pueden utilizarse para codificar una imagen binaria en cada imagen componente, como se muestra en el esquema de la derecha. Cada píxel blanco de cada imagen componente se representa con dos subpíxeles negros, mientras que cada píxel negro se representa con tres subpíxeles negros.

Al superponerse, cada píxel blanco de la imagen secreta se representa con tres subpíxeles negros, mientras que cada píxel negro se representa con cuatro subpíxeles negros. Además, cada píxel correspondiente en las imágenes componentes se rota de manera aleatoria para evitar que la orientación revele información sobre la imagen secreta.[12]​

  • En " Do Not Forsake Me Oh My Darling ", un episodio de 1967 de la serie de televisión The Prisoner, el protagonista utiliza una superposición de criptografía visual de múltiples transparencias para revelar un mensaje secreto: la ubicación de un amigo científico que se había escondido

Véase también

Referencias

  1. ↑ Naor, Moni; Shamir, Adi (1995). «Visual cryptography». Advances in Cryptology – EUROCRYPT'94. Lecture Notes in Computer Science 950. pp. 1-12. ISBN 978-3-540-60176-0. doi:10.1007/BFb0053419. 
  2. ↑ Verheul, Eric R.; Van Tilborg, Henk C. A. (1997). «Constructions and Properties of k out of n Visual Secret Sharing Schemes». Designs, Codes and Cryptography 11 (2): 179-196. doi:10.1023/A:1008280705142. 
  3. ↑ Ateniese, Giuseppe; Blundo, Carlo; Santis, Alfredo De; Stinson, Douglas R. (2001). «Extended capabilities for visual cryptography». Theoretical Computer Science 250 (1–2): 143-161. doi:10.1016/S0304-3975(99)00127-9. 
  4. ↑ Jiao, Shuming; Feng, Jun; Gao, Yang; Lei, Ting; Yuan, Xiaocong (2020). «Visual cryptography in single-pixel imaging». Optics Express 28 (5): 7301-7313. PMID 32225961. arXiv:1911.05033. doi:10.1364/OE.383240. 
  5. ↑ Gnanaguruparan, Meenakshi; Kak, Subhash (2002). «Recursive Hiding of Secrets in Visual Cryptography». Cryptologia 26: 68-76. doi:10.1080/0161-110291890768. 
  6. ↑ Cook, Richard C. (1960) Cryptographic process and enciphered product, United States patent 4,682,954.
  7. ↑ Carlson, Carl O. (1961) Information encoding and decoding method, United States patent 3,279,095.
  8. ↑ Kafri, O.; Keren, E. (1987). «Encryption of pictures and shapes by random grids». Optics Letters 12 (6): 377-9. Bibcode:1987OptL...12..377K. PMID 19741737. doi:10.1364/OL.12.000377. 
  9. ↑ Arazi, B.; Dinstein, I.; Kafri, O. (1989). «Intuition, perception, and secure communication». IEEE Transactions on Systems, Man, and Cybernetics 19 (5): 1016-1020. doi:10.1109/21.44016. 
  10. ↑ . NECEC 2011. November 2011. 
  11. ↑ Horng, Gwoboa; Chen, Tzungher; Tsai, Du-Shiau (2006). «Cheating in Visual Cryptography». Designs, Codes and Cryptography 38 (2): 219-236. doi:10.1007/s10623-005-6342-0. 
  12. ↑ M. Pramanik, Kalpana Sharma, Analysis of Visual Cryptography, Steganography Schemes and its Hybrid Approach for Security of Images, Computer Science, 2014

Enlaces externos

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons Attribution-Share Alike 4.0. Pueden aplicarse cláusulas adicionales a los archivos multimedia.