Construcción de Maxwell

En física estadística y termodinámica, la construcción de Maxwell es un método para abordar los aspectos físicamente poco realistas de ciertos modelos de transición de fase. Llamada así por el físico James Clerk Maxwell, considera áreas de regiones en diagramas de fase.

En equilibrio termodinámico, una condición necesaria para la estabilidad es que la presión, ${\displaystyle p}$, no aumente con el volumen o el volumen molar, ${\displaystyle v=V/N}$; esto se expresa matemáticamente como ${\displaystyle \partial _{v}p|_{T}<0}$, donde ${\displaystyle T}$ es la temperatura.^[1]​ Este requisito básico de estabilidad, y otros similares para otros pares de variables conjugadas, se incumple en los modelos analíticos de transición de fase de primer orden. El caso más famoso es la ecuación de van der Waals,^[2]​^[3]​ $${\displaystyle p=RT/(v-b)-a/v^{2}}$$ donde ${\displaystyle a,b,R}$ son constantes dimensionales. Esta violación no es un defecto, sino el origen de la discontinuidad observada en las propiedades que distinguen al líquido del vapor, y define una transición de fase de primer orden.

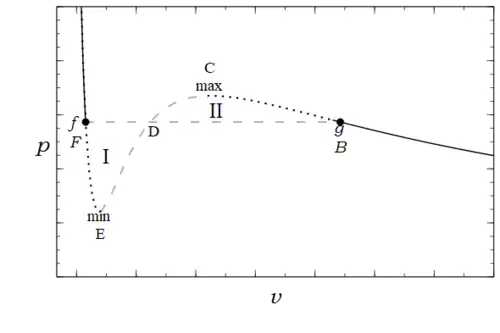
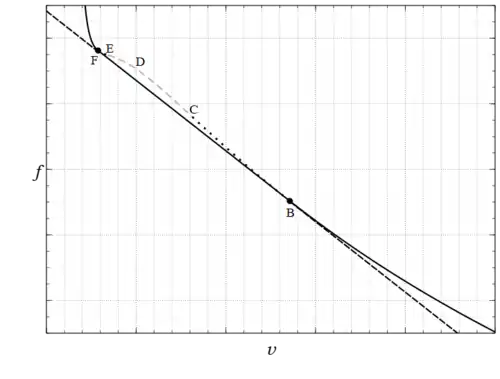
La figura 1 muestra una isoterma trazada, para ${\displaystyle v>b}$, como una curva continua diferenciable de color negro sólido, negro punteado y gris discontinuo. La parte decreciente de la curva a la derecha del punto C en la figura 1 describe un gas, mientras que la parte decreciente a la izquierda del punto E describe un líquido. Estas dos partes están separadas por una región entre el mínimo local y el máximo local de la curva con pendiente positiva que viola el criterio de estabilidad. Este criterio matemático expresa una condición física que Epstein^[4]​ describió de la siguiente manera: «Es obvio que esta parte central, punteada en nuestras curvas [rayada en la figura 1], no puede tener realidad física. De hecho, imaginemos el fluido en un estado correspondiente a esta parte de la curva contenida en un cilindro vertical conductor del calor cuya parte superior está formada por un pistón. El pistón puede deslizarse hacia arriba y hacia abajo en el cilindro, y colocamos sobre él una carga que equilibra exactamente la presión del gas. Si quitamos un poco de peso del pistón, ya no habrá equilibrio y comenzará a moverse hacia arriba. Sin embargo, a medida que se mueve, el volumen del gas aumenta y con él su presión. La fuerza resultante sobre el pistón se hace mayor, manteniendo su dirección ascendente. Por lo tanto, el pistón seguirá moviéndose y el gas se expandirá hasta alcanzar el estado representado por el máximo de la isoterma. Por el contrario, si añadimos una cantidad mínima a la carga del pistón equilibrado, el gas colapsará hasta alcanzar el estado correspondiente al mínimo de la isoterma.

Esta situación es similar a la de un cuerpo en equilibrio perfecto en la parte superior de una superficie lisa que, con la más mínima perturbación, se desvía de su posición de equilibrio y continúa hasta alcanzar un mínimo local. Tal y como se describen, estos estados son dinámicamente inestables y, por lo tanto, no se observan. La diferencia ${\displaystyle v_{\rm {min}}\leq v\leq v_{\rm {max}}}$ es un precursor del cambio de fase real de líquido a vapor. Los puntos E ${\displaystyle (p_{\rm {min}},v_{\rm {min}})}$ y C ${\displaystyle (p_{\rm {max}},v_{\rm {max}})}$, donde ${\displaystyle \partial _{v}p|_{T}=0}$, que delimitan los estados líquidos más grandes y los estados gaseosos más pequeños posibles, se denominan puntos spinodales. Su lugar geométrico forma una curva espinodal que delimita una región en la que no pueden existir estados homogéneos estables.

Los experimentos muestran que si se calienta y se expande a temperatura constante el volumen de un recipiente que contiene una cantidad fija de líquido, a una presión determinada, ${\displaystyle p_{s}(T)}$, vapor (indicado por puntos en los puntos ${\displaystyle f}$ y ${\displaystyle g}$ en la figura 1) se forman burbujas, por lo que el fluido ya no es homogéneo, sino que se ha convertido en una mezcla heterogénea de líquido en ebullición y vapor en condensación. La gravedad separa el líquido en ebullición (saturado), ${\displaystyle v_{f}=V_{f}/N_{f}}$, del vapor en condensación (saturado) menos denso, ${\displaystyle v_{\text{g}}=V_{\text{g}}/N_{\text{g}}>v_{f},}$ que coexisten a la misma temperatura y presión de saturación. A medida que continúa el calentamiento, la cantidad de vapor, ${\displaystyle N_{\text{g}}}$, aumenta y la del líquido, ${\displaystyle N_{f}=N-N_{\text{g}}}$, disminuye. Mientras tanto, la presión, ${\displaystyle p_{s}}$, y la temperatura, ${\displaystyle T}$, permanecen constantes y el volumen ${\displaystyle V=V_{f}+V_{\text{g}}}$ aumenta. En esta situación, el volumen molar de la mezcla es una media ponderada de sus componentes.

$${\displaystyle v=V/N=(V_{f}/N_{f})(N-N_{\text{g}})/N+(V_{\text{g}}/N_{\text{g}})(N_{\text{g}}/N)=v_{f}(1-x)+v_{\text{g}}x}$$

donde ${\displaystyle x=N_{\text{g}}/N}$, la fracción molar del vapor, ${\displaystyle 0\leq x\leq 1}$, aumenta continuamente; sin embargo, el volumen molar de la sustancia en sí solo tiene el mayor valor estable posible para su estado líquido y el menor valor estable posible para su estado gaseoso a la ${\displaystyle p(T)}$ dada. Repitiendo, aunque el volumen molar de la mezcla pasa continuamente de ${\displaystyle v_{f}}$ a ${\displaystyle v_{\text{g}}}$ (indicado por la línea discontinua en la figura 1), el fluido subyacente presenta una discontinuidad en esta propiedad, así como en otras. Esta ecuación de estado de la mezcla se denomina regla de la palanca.^[5]​^[6]​^[7]​

Las partes punteadas de la curva de la figura 1 son estados metaestables. Durante muchos años, estos estados fueron una curiosidad académica; Callen^[8]​ dio como ejemplo «el agua que se ha enfriado por debajo de 0 °C a una presión de 1 atm. Al golpear un vaso de precipitados con agua en estas condiciones, se produce una cristalización repentina y espectacular del sistema». Sin embargo, los estudios sobre la transferencia de calor por ebullición han dejado claro que los estados metaestables se producen habitualmente como parte integrante de este proceso. En él, la temperatura de la superficie de calentamiento es superior a la temperatura de saturación, a menudo de forma significativa, por lo que el líquido adyacente debe estar sobrecalentado.^[9]​ Además, la aparición de dispositivos que funcionan con flujos de calor muy elevados ha despertado el interés por los estados metaestables y las propiedades termodinámicas asociadas a ellos, en particular los estados líquidos sobrecalentados.^[10]​ Por otra parte, el hecho de que sean predecibles por la ecuación de van der Waals y, en general, por ecuaciones cúbicas, es una prueba convincente de su eficacia para describir las transiciones de fase. Sommerfeld lo describió de la siguiente manera:^[11]​

Es muy notable que la teoría de van der Waals sea capaz de predecir, al menos cualitativamente, la existencia de estados inestables [denominados aquí metaestables] a lo largo de las ramas «AA»′ o «BB»′ [BC y FE en la figura 1].

La discontinuidad en ${\displaystyle v}$ y otras propiedades, por ejemplo, la energía interna, ${\displaystyle u}$, y la entropía, ${\displaystyle s}$, de la sustancia, se denomina transición de fase de primer orden.^[12]​^[13]​ Para especificar la presión única observada experimentalmente, ${\displaystyle p_{s}(T)}$, a la que se produce, se requiere otra condición termodinámica, ya que, según la figura 1, podría producirse claramente para cualquier presión en el intervalo ${\displaystyle p_{\rm {min}}\leq p\leq p_{\rm {max}}}$. Esta condición fue enunciada por primera vez en un ingenioso argumento termodinámico por Maxwell en una conferencia que impartió en la British Chemical Society el 18 de febrero de 1875^[14]​ (la figura 1, que incluye las letras B, C, D, E y F, es la curva que describió):

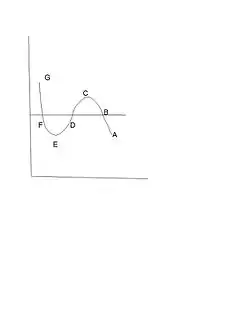
La parte de la curva desde «C» hasta «E» representa puntos que son esencialmente inestables y que, por lo tanto, no pueden realizarse. Ahora supongamos que el medio pasa de «B» a «F» siguiendo la curva hipotética «B» «C» «D» «E» «F» en un estado siempre homogéneo, y que regresa siguiendo la línea recta «F» «B» en forma de mezcla de líquido y vapor. Dado que la temperatura ha sido constante durante todo el proceso, no se ha transformado calor en trabajo. Ahora bien, el calor transformado en trabajo está representado por el exceso del área «F» «D» «E» sobre «B» «C» «D». Por lo tanto, la condición que determina la presión máxima del vapor a una temperatura dada es que la línea «B» «F» corte áreas iguales de la curva por encima y por debajo.

En un plano de temperatura-entropía molar, el área bajo cualquier curva es la transferencia de calor a la sustancia por mol, siendo positiva de izquierda a derecha y negativa de derecha a izquierda; además, en un proceso cíclico, la transferencia neta de calor a la sustancia es el área encerrada por la curva cerrada del ciclo.^[15]​^[16]​ Dado que el ciclo considerado por Maxwell está compuesto por las dos isotérmicas grises discontinuas a la misma temperatura, una que va de B a F (pasando por C, D y E) y la otra que vuelve directamente de F a B, las dos líneas son idénticas, solo que se recorren en sentido inverso; no hay área encerrada y, por lo tanto, ${\displaystyle q=0}$.

Además, el área bajo estas curvas cuando se trazan en una presión-volumen molar, véase la figura 1, es el trabajo realizado por la sustancia, positivo de izquierda a derecha y negativo de derecha a izquierda. Del mismo modo, el trabajo neto realizado en un ciclo es el área encerrada por la curva cerrada. Dado que la primera ley de la termodinámica da como resultado, en el caso especial de un ciclo, ${\displaystyle w=q}$, para el ciclo previsto por Maxwell ${\displaystyle w=q=0}$; entonces, dado que el área encerrada es I + II = 0, véase la figura 1, con I positivo y II negativo, la presión de transición debe ser tal que las dos áreas sean iguales.

Expresado como una ecuación matemática en términos del trabajo realizado en cada proceso, esto es $${\displaystyle \int _{v_{\text{g}}}^{v_{f}}\,p\,dv+\int _{v_{f}}^{v_{\text{g}}}\,p_{s}\,dv=-\int _{v_{f}}^{v_{\text{g}}}\,p\,dv+p_{s}(v_{\text{g}}-v_{f})=0\quad {\mbox{para}}\quad T={\mbox{constante}}}$$

Esta ecuación, junto con la ecuación de estado escrita para cada uno de los estados ${\displaystyle f}$ y ${\displaystyle g}$ $${\displaystyle p_{s}=p(v_{f},T)\qquad p_{s}=p(v_{\text{g}},T)}$$ son tres ecuaciones para las cuatro variables, ${\displaystyle p_{s},T,v_{f},v_{\text{g}}}$, por lo que, dada cualquiera de ellas, por ejemplo ${\displaystyle T}$, las otras tres quedan determinadas. En otras palabras, existe un valor único de ${\displaystyle p_{s}(T)}$, así como de ${\displaystyle v_{f}(T)}$ y ${\displaystyle v_{\text{g}}(T)}$, en el que puede producirse la transición de fase.

Al final de su conferencia, tras elogiar a van der Waals refiriéndose a su trabajo como «una tesis sumamente ingeniosa», Maxwell concluyó diciendo:

No obstante, no puedo dejar de mencionar una contribución estadounidense muy importante a esta parte de la termodinámica, realizada por el profesor Willard Gibbs del Yale College (EE. UU.), quien nos ha proporcionado un método extraordinariamente sencillo y totalmente satisfactorio para representar las relaciones entre los diferentes estados de la materia mediante un modelo. Gracias a este modelo, problemas que durante mucho tiempo habían resistido los esfuerzos míos y de otros pueden resolverse de inmediato.

Esta observación resultó profética, ya que en 1876-1878 Gibbs publicó su obra definitiva sobre termodinámica^[17]​ en la que demostró que el equilibrio termodinámico de una sustancia heterogénea requiere que, además del equilibrio mecánico (la misma presión para cada componente) y el equilibrio térmico (la misma temperatura para cada componente), también debe existir el equilibrio material (el mismo potencial químico para cada componente). En el presente caso de una sustancia y dos fases, además de ${\displaystyle p_{f}=p_{\text{g}}=p_{s}}$ y ${\displaystyle T_{f}=T_{\text{g}}=T}$, el equilibrio material requiere ${\displaystyle g_{f}=g_{\text{g}}}$ (para el caso especial de una sustancia, su potencial químico es la función molar de Gibbs, ${\displaystyle \mu =g\equiv G/N}$ donde ${\displaystyle g=u+pv-Ts}$).^[18]​ Esta condición se puede deducir mediante un sencillo razonamiento físico, como se explica a continuación: la energía necesaria para vaporizar un mol se obtiene a partir de la segunda ley a temperatura constante ${\displaystyle q_{\rm {vap}}=T(s_{\text{g}}-s_{f})}$, y de la primera ley a presión constante ${\displaystyle q_{\rm {vap}}=h_{\text{g}}-h_{f}}$, luego, igualando estas dos y reorganizándolas se obtiene el resultado, ya que ${\displaystyle h=u+pv}$. Las condiciones de equilibrio de los materiales conducen a la famosa regla de las fases de Gibbs, ${\displaystyle D=n-r+2}$, donde ${\displaystyle n}$ es el número de sustancias, ${\displaystyle r}$ el número de fases y ${\displaystyle D}$ el número de variables intensivas independientes necesarias para especificar el estado.^[19]​^[20]​ En el caso de una sustancia y dos fases que se analiza aquí, esto da ${\displaystyle D=1}$, el número observado experimentalmente.

Ahora, ${\displaystyle g(p,T)}$ es una función potencial termodinámica, su derivada es^[21]​ $${\displaystyle dg=\partial _{p}g|_{T}\,dp+\partial _{T}g|_{p}\,dT=v\,dp-s\,dT}$$

Al integrar esto a temperatura constante se obtiene $${\displaystyle g(p,T)=g_{A}(T)+\int _{p_{A}}^{p}\,v({\bar {p}},T)\,d{\bar {p}}}$$ donde ${\displaystyle g_{A}}$ es una constante de integración, pero la constante es diferente para cada isoterma, por lo que se escribe como una función de ${\displaystyle T}$.^[22]​ Para evaluar ${\displaystyle g}$, hay que invertir ${\displaystyle p=p(v,T)}$ para obtener ${\displaystyle v=v(p,T)}$. Sin embargo, es propia de la naturaleza del fenómeno de transición de fase que esta inversión no sea única; por ejemplo, la ecuación de van der Waals escrita para ${\displaystyle v}$ es: $${\displaystyle pv^{3}-(pb+RT)v^{2}+av-ab=0,}$$

una cúbica con 1 o, en este caso, 3 raíces reales. Por lo tanto, hay tres curvas, como se ve en la Fig. 2, que consisten en estados estables (mostrados en negro sólido), metaestables (mostrados en negro punteado) e inestables (mostrados en gris discontinuo).

En realidad, la figura no se obtuvo resolviendo la ecuación cúbica e integrando, sino que ${\displaystyle g(v,T)}$ se obtuvo a partir de su definición, obteniendo primero ${\displaystyle u(v,T)}$ y ${\displaystyle s(v,T)}$, lo cual es fácil de hacer analíticamente para la ecuación de van der Waals, y representándola paramétricamente con ${\displaystyle p(v,T)}$, utilizando ${\displaystyle v}$ como parámetro. Teniendo en cuenta solo sus estados estables, ${\displaystyle g(p,T)}$ es continua con derivadas parciales discontinuas, ${\displaystyle \partial _{p}g|_{T}=v}$ y ${\displaystyle \partial _{T}g|_{p}=-s}$, en el punto de transición de fase. En la clasificación Ehrenfest , una transición de fase de primer orden se refiere a la discontinuidad de las primeras derivadas parciales de ${\displaystyle g}$, mientras que una transición de fase de segundo orden implicaría discontinuidades de las segundas derivadas parciales.^[23]​

Para evaluar la expresión integral de ${\displaystyle g(p,T)}$ dada anteriormente entre los estados líquido y vapor saturados y aplicar el criterio de Gibbs de equilibrio material a este proceso de cambio de fase, es necesario escribirla como $${\displaystyle g_{\text{g}}-g_{f}=\int _{p_{s}}^{p_{\rm {min}}}\,v_{l}\,dp+\int _{p_{\rm {min}}}^{p_{\rm {max}}}\,v_{u}\,dp+\int _{p_{\rm {max}}}^{p_{s}}\,v_{v}\,dp=0}$$

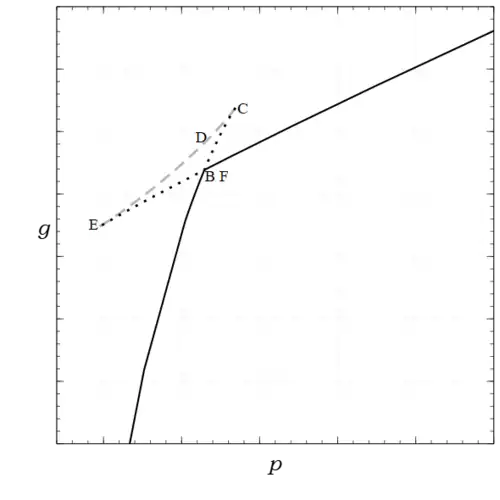
Aquí, la integral se ha dividido en tres partes utilizando las tres raíces reales de la cúbica correspondientes a los estados líquido, ${\displaystyle v_{l}}$, inestable, ${\displaystyle v_{u}}$, y vapor, ${\displaystyle v_{v}}$, respectivamente. Estas integrales se pueden visualizar mejor girando la figura 1 ${\displaystyle 90^{\circ }}$ en sentido antihorario en el plano del papel y luego ${\displaystyle 180^{\circ }}$ alrededor del eje ${\displaystyle v}$, de modo que ${\displaystyle v}$ aparezca en el eje de ordenadas izquierdo de la curva, como se muestra en el gráfico adjunto. En esta vista, la función ${\displaystyle v(p,T)}$ es claramente multivaluada; esta es la razón por la que se necesitan tres funciones reales para describir su comportamiento entre ${\displaystyle p_{\rm {min}}}$ y ${\displaystyle p_{\rm {max}}}$. Ahora, al dividir la integral del medio en dos $${\displaystyle g_{\text{g}}-g_{f}=\int _{p_{s}}^{p_{\rm {min}}}\,v_{l}\,dp+\int _{p_{\rm {min}}}^{p_{s}}\,v_{u}\,dp+\int _{p_{s}}^{p_{\rm {max}}}\,v_{u}\,dp+\int _{p_{\rm {max}}}^{p_{s}}\,v_{v}\,dp=0}$$

Las dos primeras integrales aquí son el área I, mientras que las dos segundas son el negativo del área II. Las dos áreas suman cero, por lo que sus magnitudes son iguales según este criterio de Gibbs. Se trata, una vez más, de la regla del área igual de Maxwell, la construcción de Maxwell, y también se puede demostrar analíticamente. Dado que ${\displaystyle d(pv)=pdv+vdp}$, $${\displaystyle dg=v\,dp-s\,dT=-p\,dv+d(pv)-s\,dT.}$$

Al integrar esto para una temperatura constante desde el estado ${\displaystyle f}$ al estado ${\displaystyle g}$ con la condición de Gibbs, se obtiene $${\displaystyle g_{\text{g}}-g_{f}=-\int _{v_{f}}^{v_{\text{g}}}\,p(v,T)\,dv+p_{s}(v_{\text{g}}-v_{f})=0}$$ que es el resultado de Maxwell. Esta regla del área igual también se puede derivar utilizando la energía libre de Helmholtz.^[24]​ En cualquier caso, la construcción de Maxwell se deriva de la condición de Gibbs de equilibrio material. Sin embargo, aunque ${\displaystyle g_{f}=g_{\text{g}}}$ es más fundamental, es más abstracto que la regla del área igual, que se entiende geométricamente.

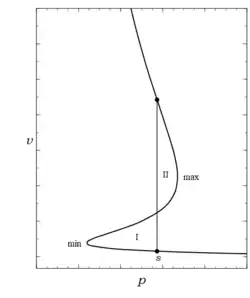
Otro método para determinar los puntos de coexistencia se basa en el principio del mínimo potencial de Helmholtz, que establece que en un sistema en contacto diatérmico con un reservorio de calor ${\displaystyle T=T_{R}}$, ${\displaystyle DF=0}$ y ${\displaystyle D^{2}F>0}$, es decir, en equilibrio, el potencial de Helmholtz es mínimo.^[25]​ Dado que, al igual que ${\displaystyle g(p,T)}$, la función molar de Helmholtz ${\displaystyle f(v,T)}$ es también una función potencial cuya derivada es,^[26]​ $${\displaystyle df=\partial _{v}f|_{T}\,dv+\partial _{T}f|_{v}\,dT=-p\,dv-s\,dT,}$$

Este principio mínimo conduce a la condición de estabilidad ${\displaystyle \partial ^{2}f/\partial v^{2}|_{T}=-\partial p/\partial v|_{T}>0}$.^[27]​ Esta condición requiere que, en cualquier estado estable del sistema, la función ${\displaystyle f}$ sea estrictamente convexa, es decir, que en su vecindad la curva se encuentre en su tangente o por encima de ella.^[28]​ Además, para esos estados, también se cumple necesariamente la condición de estabilidad anterior para la presión.

En la figura 3 se muestra un gráfico de esta función para la misma isoterma subcrítica de la ecuación de vdW que en las figuras 1 y 2. En esta figura se incluye la línea recta (discontinua/continua) que tiene una tangente doble (común) con la curva de la función ${\displaystyle f}$ en B y F. Esta línea recta es

${\displaystyle f=f_{0}+\partial _{v}f_{T}v=f_{0}-pv}$, con ${\displaystyle p}$ constante, que puede escribirse como ${\displaystyle f_{0}=f+pv=g}$. La última igualdad se deduce de la relación ${\displaystyle f=u-Ts}$,^[29]​ junto con ${\displaystyle g=u-Ts+pv}$.^[18]​ Todo esto significa que cada punto de la línea tiene los mismos valores de ${\displaystyle g,p,T}$, en particular los puntos B y F, lo que produce la condición de Gibbs para el equilibrio material ${\displaystyle g_{f}=g_{\text{g}}}$, así como la igualdad de temperatura y presión.^[30]​ Por lo tanto, esta construcción es equivalente tanto a las condiciones de Gibbs como a la construcción de Maxwell.

Esta construcción, basada en ${\displaystyle f(v,T)}$ definida anteriormente por Gibbs,^[31]​^[32]​, fue utilizada originalmente por van der Waals (que la denominó «tangente doble y común»),^[33]​ porque podía extenderse fácilmente para incluir fluidos binarios mezclas para los que una isoterma de ${\displaystyle f(v,x,T)}$, con ${\displaystyle x=N_{1}/(N_{1}+N_{2})}$ como variable de composición, forma una superficie que puede tener un plano tangente común. Posteriormente, se ha convertido en una forma popular de tratar los problemas de cambio de fase en mezclas.^[34]​^[35]​^[36]​

A partir de la ecuación de van der Waals aplicada al líquido saturado, ${\displaystyle v_{f}<v_{\rm {min}}}$, y al vapor, ${\displaystyle v_{\text{g}}>v_{\rm {max}}}$, se obtienen $${\displaystyle p_{s}={\frac {RT_{s}}{v_{f}-b}}-{\frac {a}{v_{f}^{2}}}\qquad p_{s}={\frac {RT_{s}}{v_{\text{g}}-b}}-{\frac {a}{{v_{\text{g}}}^{2}}}}$$

Estas dos ecuaciones especifican 4 variables, por lo que pueden resolverse para ${\displaystyle p_{s},T_{s}}$ en términos de ${\displaystyle v_{f},v_{\text{g}}}$. This results in $${\displaystyle p_{s}=p^{*}{\frac {v^{*2}[v_{f}v_{\text{g}}-v^{*}(v_{f}+v_{\text{g}})]}{v_{f}^{2}{v_{\text{g}}}^{2}}}\qquad T_{s}=T^{*}{\frac {v^{*}(v_{f}+v_{\text{g}})(v_{f}-v^{*})(v_{\text{g}}-v^{*})}{v_{f}^{2}{v_{\text{g}}}^{2}}}}$$ donde ${\displaystyle p^{*}=a/b^{2}}$, ${\displaystyle v^{*}=b}$ y ${\displaystyle T^{*}=a/(Rb)}$ son una presión característica, un volumen molar y una temperatura definidos por las constantes (tenga en cuenta que ${\displaystyle p^{*}v^{*}/T^{*}=R}$). Al aplicar la construcción de Maxwell a la ecuación de van der Waals se obtiene $${\displaystyle -T_{s}\ln \left({\frac {v_{\text{g}}-v^{*}}{v_{f}-v^{*}}}\right)+T^{*}{\frac {v^{*}(v_{\text{g}}-v_{f})}{v_{f}v_{\text{g}}}}+p_{s}(v_{\text{g}}-v_{f})/R=0}$$

Estas tres ecuaciones pueden resolverse numéricamente. Esto se ha hecho dando un valor a ${\displaystyle T_{s}}$ o a ${\displaystyle p_{s}}$, y se han presentado los resultados en forma de tabla;^[37]​^[38]​ sin embargo, las ecuaciones también admiten una solución paramétrica analítica que, según Lenkner,^[39]​ fue obtenida por Gibbs. El propio Lenkner ideó un método sencillo y elegante para obtener esta solución, eliminando ${\displaystyle p_{s}}$ y ${\displaystyle T_{s}}$ de las ecuaciones y escribiéndolas en términos de una densidad adimensional estirada, ${\displaystyle \varrho =v^{*}/(v-v^{*})}$, que varía entre ${\displaystyle \infty }$ y 0 a medida que ${\displaystyle v}$ varía de ${\displaystyle v^{*}}$ a ${\displaystyle \infty }$; esto produce $${\displaystyle \ln \left({\frac {\varrho _{f}}{\varrho _{\text{g}}}}\right)={\frac {(\varrho _{f}-\varrho _{\text{g}})(\varrho _{\text{g}}+\varrho _{f}+2)}{\varrho _{f}+\varrho _{\text{g}}+2\varrho _{f}\varrho _{\text{g}}}}}$$

Aunque trascendental, esta ecuación tiene una solución analítica y paramétrica sencilla que se obtiene escribiendo el lado izquierdo de la ecuación, que es simplemente ${\displaystyle (s_{\text{g}}-s_{f})/R}$, como $${\displaystyle \ln \left({\frac {\varrho _{f}}{\varrho _{\text{g}}}}\right)={\frac {s_{\text{g}}-s_{f}}{R}}=\delta =2y}$$

Entonces ${\displaystyle \varrho _{f}=e^{\delta }\varrho _{\text{g}}}$ y, al utilizarlo para eliminar ${\displaystyle \varrho _{f}}$ del lado derecho, se obtiene una ecuación lineal para ${\displaystyle \varrho _{\text{g}}}$, cuya solución es $${\displaystyle \varrho _{\text{g}}(y)=f(y)e^{-y}\quad {\mbox{y}}\quad \varrho _{f}(y)=f(y)e^{y}\quad {\mbox{donde}}\quad f(y)={\frac {y\cosh y-\sinh y}{\sinh y\cosh y-y}}}$$

Por consiguiente, la variable fundamental que especifica todas las demás en este proceso de transición de fase es ${\displaystyle (s_{\text{g}}-s_{f})/(2R)=y}$. Esta solución al problema de saturación se extiende fácilmente para abarcar todas sus variables $${\displaystyle T_{s}(y)=T^{*}{\frac {2f(y)[\cosh y+f(y)]}{g(y)^{2}}}\qquad p_{s}(y)=p^{*}{\frac {f(y)^{2}[1-f(y)^{2}]}{g(y)^{2}}}}$$ $${\displaystyle v_{f}(y)=v^{*}{\frac {1+f(y)e^{y}}{f(y)e^{y}}}\quad \quad \quad \quad \quad \quad v_{g}(y)=v^{*}{\frac {1+f(y)e^{-y}}{f(y)e^{-y}}}}$$ where ${\displaystyle g(y)=[1+\varrho _{\text{g}}(y)][1+\varrho _{f}(y)]=1+2f(y)\cosh y+f(y)^{2}}$.

The values of all other property discontinuities across the saturation curve also follow from this solution.^[40]​

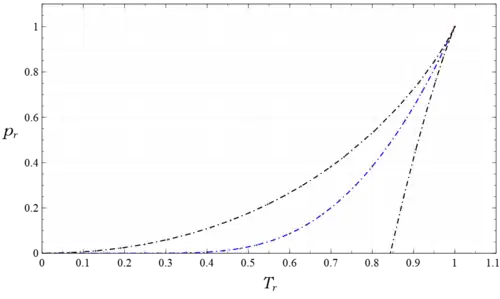
Estas funciones definen la curva de coexistencia, que es el lugar geométrico de los estados líquido saturado y vapor saturado del fluido de van der Waals. 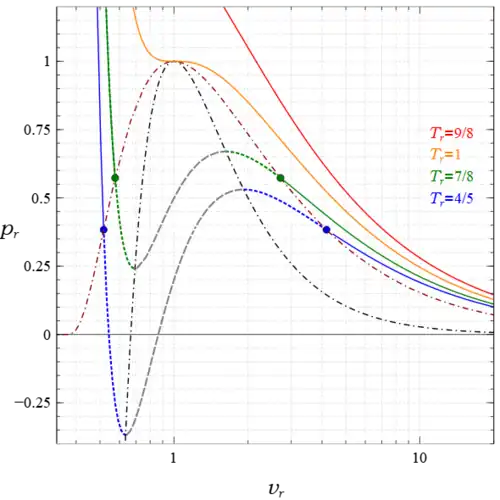En la figura 4, esta curva se representa en azul junto con la curva espinodal en negro, calculada a partir de $${\displaystyle T=T^{*}({\tilde {v}}-1)^{2}/{\tilde {v}}^{3}\quad \quad p=p^{*}({\tilde {v}}-2)/{\tilde {v}}^{3}}$$ donde ${\displaystyle {\tilde {v}}=v/v^{*}}$ es un parámetro. Las variables utilizadas para trazar estos gráficos son las variables reducidas (adimensionales), ${\displaystyle p_{r}=p/p_{c}}$, ${\displaystyle v_{r}=v/v_{c}}$ y ${\displaystyle T_{r}=T/T_{c}}$, donde las cantidades con el subíndice ${\displaystyle c}$ son los valores del punto crítico. Se definen por ${\displaystyle \partial p/\partial v|_{T}=0}$ y ${\displaystyle \partial ^{2}p/\partial _{v^{2}}|_{T}=0}$ en el punto crítico,^[41]​ y son cantidades medibles. Las relaciones ${\displaystyle p^{*}/p_{c}=27}$, ${\displaystyle v^{*}/v_{c}=1/3}$, ${\displaystyle T^{*}/T_{c}=27/8}$ se utilizan para convertir las cantidades marcadas con asterisco en la solución a las cantidades ${\displaystyle c}$ utilizadas en las figuras. La curva coincide completamente con los resultados numéricos mencionados anteriormente. En la región dentro de la curva espinodal hay dos estados en cada punto, uno estable y otro metaestable, ya sea líquido sobrecalentado a la derecha de la curva azul o vapor subenfriado a la izquierda, mientras que fuera de la curva espinodal hay un estado estable en cada punto. En la figura 5, la región situada bajo la curva espinodal (negra punteada) no contiene estados estables homogéneos, mientras que entre las curvas de coexistencia (rojas punteadas) y espinodal hay un estado metaestable en cada punto, y fuera de la curva de coexistencia hay un estado estable en cada punto. Los dos círculos azules y los dos verdes indican los estados saturados de líquido y vapor en sus respectivas isotermas. También se observan estados heterogéneos en todas partes bajo la curva de coexistencia que satisfacen la regla de la palanca; sin embargo, no son estados homogéneos de la ecuación de van der Waals, por lo que su existencia, indicada por líneas horizontales que conectan los puntos de saturación en cada isotermas subcrítica, no se muestra. Además, la abscisa de esta figura es logarítmica, no lineal, con el fin de mostrar más de la región de vapor en ${\displaystyle v_{r}}$ grande sin comprimir excesivamente las regiones líquidas e inestables en ${\displaystyle v_{r}}$ pequeño; sin embargo, este dispositivo distorsiona las áreas, por lo que las dos áreas I y II de la figura 1 no aparecerían iguales aquí.

En el rango de parámetros ${\displaystyle 0\leq y<\infty }$, ${\displaystyle f(y)}$ disminuye monótonamente desde ${\displaystyle f(0)=1}$ y se aproxima a 0 como${\displaystyle f(y)\sim 2(y-1)e^{-y}}$ en el límite ${\displaystyle y\rightarrow \infty }$. Por lo tanto, ${\displaystyle \varrho _{f}(0)=\varrho _{\text{g}}(0)=1/2}$ y, en el límite ${\displaystyle y\rightarrow \infty }$, ${\displaystyle \varrho _{f}(y)\sim 2(y-1)}$ y ${\displaystyle \varrho _{\text{g}}(y)\sim 2(y-1)e^{-2y}}$. El comportamiento de ${\displaystyle p_{s}(y)}$ y ${\displaystyle T_{s}(y)}$ se deduce de las ecuaciones. Ambas propiedades también disminuyen monótonamente desde ${\displaystyle p_{s}(0)=p^{*}/27}$ y ${\displaystyle T_{s}(0)=8T^{*}/27}$, y se aproximan a 0 a medida que ${\displaystyle p_{s}\sim p^{*}\varrho _{\text{g}}/\varrho _{f}}$ y ${\displaystyle T_{s}\sim T^{*}/\varrho _{f}}$ en el límite ${\displaystyle y\rightarrow \infty }$. De ello se deduce que ${\displaystyle p_{s}\sim (p^{*}/T^{*})T_{s}\varrho _{\text{g}}\sim (p^{*}v^{*}/T^{*})T_{s}\rho _{\text{g}}=\rho _{\text{g}}RT_{s}}$; el vapor saturado de van der Waals es un gas ideal en este límite. Parafraseando a Sommerfeld, es notable que la teoría de van der Waals sea capaz de predecir que cuando ${\displaystyle s_{\text{g}}-s_{f}\gg 2R}$ el vapor saturado se comporta como un gas ideal; el vapor saturado de los gases reales se comporta exactamente así.

Además, para ${\displaystyle T_{r}<27/32=0,84375}$, el punto espinodal líquido se produce a una presión negativa, y la isoterma ${\displaystyle T_{r}=0,8}$ se incluye en la figura 4 para ilustrar este punto. Esto significa que una parte de esos estados metestables líquidos están en tensión, y cuanto menor es la temperatura, mayor es la tensión. Aunque esto parece contrario a la intuición, se sabe que, en determinadas circunstancias, los líquidos pueden soportar tensión. Tien y Lienhard^[42]​ señalaron este hecho y escribieron:

La ecuación de van der Waals predice que, a bajas temperaturas, los líquidos soportan una enorme «tensión», un hecho que ha llevado a algunos autores a tomarse la ecuación a la ligera. En los últimos años se han realizado mediciones que revelan que esto es totalmente cierto.^[43]​ Los líquidos limpios y libres de gases disueltos pueden estar sometidos a tensiones mayores que ${\displaystyle p_{\text{c}}}$.

Esta es otra característica interesante de la teoría de van der Waals.

• Barrufet, M.A.; Eubank, P.T. (1989). «Generalized Saturation Properties of Pure Fluids Via Cubic Equations of State». Chemical Engineering Education 23 (3): 168-175. 
• Callen, H.B. (1960). Thermodynamics. NY: John Wiley and Sons. 
• DeBoer, J. (1974). «Van der Waals in his time and the present revival opening address». Physica 73 (1): 1-27. Bibcode:1974Phy....73....1D. doi:10.1016/0031-8914(74)90223-7. 
• Epstein, P.S. (1937). Textbook of Thermodynamics. NY: John Wiley and Sons. 
• Gibbs, J.W. (1928). «On the Equilibrium of heterogeneous Substances». En Longley, W.R.; Van Name, R.G., eds. The Collected Works of J. Willard Gibbs Volume I Thermodynamics (1948 edición). New Haven: Yale University Press. pp. 55-353. 
• Goodstein, D.L. (1985). States of Matter. NY: Dover. 
• Johnston, D.C. (2014). Advances in Thermodynamics of the van der Waals Fluid. Bibcode:2014atvd.book.....J. ISBN 978-1-627-05532-1. arXiv:1402.1205. doi:10.1088/978-1-627-05532-1. 
• Kondepudi, Dilip; Prigogine, Ilya (31 de diciembre de 2014). Modern Thermodynamics: From Heat Engines to Dissipative Structures (en inglés). John Wiley & Sons. ISBN 9781118371817. 
• Köpf, Michael Hubert (15 de enero de 2013). «First order phase transitions and the dynamics of spinodal decomposition». www.mhkoepf.de. Consultado el 12 de noviembre de 2019. 
• Lekner, J. (1982). «Parametric solution of the van der Waals liquid–vapor coexistence curve». Am. J. Phys. 50 (2): 161-163. Bibcode:1982AmJPh..50..161L. doi:10.1119/1.12877. 
• Lienhard, J.H. IV; Lienhard, J.H. V (2019). A Heat Transfer Textbook (Fifth edición). Mineola, NY: Dover Publications Inc. 
• Lienhard, J.H. (1986). «The Properties and Behavior of Superheated Liquids». Lat. Am. J. Heat and Mass Transfer 10: 169-187. 
• Maxwell, J.C. (1875). «On the Dynamical Evidence of the Molecular Constitution of Bodies». Nature 11 (279): 357-359. Bibcode:1875Natur..11..357C. doi:10.1038/011357a0. 
• Moran, M.J.; Shapiro, H.N. (2000). Fundamentals of Engineering Thermodynamics (4th edición). NY: McGraw-Hill. 
• Rectorys, K. (1969). «Differential Calculus of Functions of a Real Variable». En Rectories, K., ed. Survey of Applicable Mathematics. Cambridge, MA: The M.I.T. Press. pp. 397-439. 
• Shamsundar, N.; Lienhard, J.H. (1983). «Saturation and Metastable Properties of the van der Waals Fluid». Can J Chem Eng 61 (6): 876-880. doi:10.1002/cjce.5450610617. 
• Sommerfeld, A. (1956). Bopp, F.; Meixner, J., eds. Thermodynamics and Statistical Mechanics - Lectures on Theoretical Physics Volume V. NY: Academic Press. 
• Temperley, H N V. (1947). «The behaviour of water under hydrostatic tension: III». Proceedings of the Physical Society 59 (2): 199-208. Bibcode:1947PPS....59..199T. doi:10.1088/0959-5309/59/2/304. 
• Tien, C.L.; Lienhard, J.H. (1979). Statistical Thermodynamics Revised Printing. NY: Hemisphere Publishing. Bibcode:1979wdch.book.....T. 
• Van Wylen, G.J.; Sonntag, R.E. (1973). Fundamentals of Classical Thermodynamics (Second edición). NY: John Wiley and Sons. 
• van der Waals, J.D. (1984). Rowlinson, J.S., ed. On the Continuity of the Gaseous and Liquid States, edited and with an Introduction by J.S. Rowlinson. NY: Dover Phoenix Editions. 
• Wales, David (2003). Energy Landscapes: Applications to Clusters, Biomolecules and Glasses (en inglés). Cambridge University Press. p. 444. ISBN 9780521814157.