Constantes de línea primaria

Las constantes de línea primarias son parámetros que describen las características de las líneas de transmisión conductoras, como los pares de hilos de cobre, en términos de las propiedades eléctricas físicas de la línea. Las constantes de línea primarias sólo son relevantes para las líneas de transmisión y deben contrastarse con las constantes de línea secundarias, que pueden derivarse de ellas y son de aplicación más general. Las constantes de línea secundarias pueden utilizarse, por ejemplo, para comparar las características de una guía de ondas con las de una línea de cobre, mientras que las constantes primarias no tienen ningún significado para una guía de ondas.

Las constantes son la resistencia y la inductancia del conductor, y la capacitancia y conductancia del aislante, que por convención reciben los símbolos R, L, C y G respectivamente. Las constantes se enumeran en términos de longitud unitaria. La representación en circuito de estos elementos requiere un modelo de elementos distribuidos y, en consecuencia, debe utilizarse el cálculo para analizar el circuito. El análisis da lugar a un sistema de dos ecuaciones diferenciales parciales lineales simultáneas de primer orden que pueden combinarse para obtener las constantes secundarias de impedancia característica y constante de propagación.

Algunos casos especiales tienen soluciones especialmente sencillas e importantes aplicaciones prácticas. Los cables de bajas pérdidas sólo requieren incluir L y C en el análisis, lo que resulta útil para longitudes cortas de cable. Las aplicaciones de baja frecuencia, como las líneas telefónicas de par trenzado, están dominadas únicamente por R y C. Las aplicaciones de alta frecuencia, como el cable coaxial de RF, están dominadas por L y C. Las líneas cargadas para evitar la distorsión necesitan los cuatro elementos en el análisis, pero tienen una solución sencilla y elegante.

Hay cuatro constantes de línea principales, pero en algunas circunstancias algunas de ellas son lo suficientemente pequeñas como para ignorarlas y simplificar el análisis. Estas cuatro, y sus símbolos y unidades, son las siguientes:

R y L son elementos en serie con la línea (porque son propiedades del conductor) y C y G son elementos de derivación de la línea (porque son propiedades del material dieléctrico entre los conductores). G representa la corriente de fuga a través del dieléctrico y en la mayoría de los cables es muy pequeña. La palabra bucle se utiliza para subrayar que hay que tener en cuenta la resistencia y la inductancia de ambos conductores. Por ejemplo, si una línea está formada por dos conductores idénticos que tienen una resistencia de 25 mΩ/m cada uno, la resistencia de bucle es el doble, 50 mΩ/m. Como los valores de las constantes son bastante pequeños, es habitual que los fabricantes las citen por kilómetro en lugar de por metro; en el mundo anglosajón también se puede utilizar "per mile".^[1]​^[2]​

La palabra "constante" puede inducir a error. Significa que son constantes materiales, pero pueden variar con la frecuencia. En particular, R está muy influida por el efecto piel. Además, aunque G no tiene prácticamente ningún efecto a la frecuencia de audio, puede causar pérdidas notables a alta frecuencia con muchos de los materiales dieléctricos utilizados en los cables debido a una tangente de pérdida elevada. Evitar las pérdidas causadas por G es la razón por la que muchos cables diseñados para su uso en UHF están aislados por aire o espuma (lo que los hace prácticamente aislados por aire).^[3]​El significado real de constante en este contexto es que el parámetro es constante con la distancia. Es decir, se supone que la línea es homogénea longitudinalmente. Esta condición se cumple en la gran mayoría de las líneas de transmisión que se utilizan hoy en día.^[4]​

Los fabricantes suelen omitir el valor de la inductancia en sus hojas de datos. Algunos de estos valores se estiman a partir de las cifras de capacitancia e impedancia característica mediante 𝑍02=𝐿/𝐶.

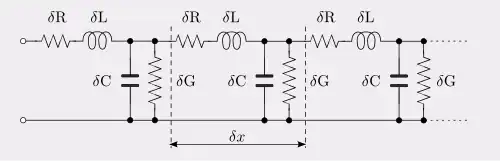
Las constantes de línea no pueden representarse simplemente como elementos agrupados en un circuito, sino que deben describirse como elementos distribuidos. Por ejemplo, "trozos" de la capacitancia están entre "trozos" de la resistencia. Por muchos trozos en que se dividan la R y la C, siempre se puede argumentar que deberían dividirse aún más para representar adecuadamente el circuito, y después de cada división se aumenta el número de mallas del circuito. Esto se muestra en la figura 1. Para obtener una representación real del circuito, los elementos deben hacerse infinitesimalmente pequeños, de modo que cada elemento se distribuya a lo largo de la línea. Los elementos infinitesimales en una distancia infinitesimal 𝑑𝑥 vienen dados por;^[14]​

${\displaystyle dL=\lim _{\delta x\to 0}(L\delta x)=Ldx}$

${\displaystyle dR=\lim _{\delta x\to 0}(R\delta x)=Rdx}$

${\displaystyle dC=\lim _{\delta x\to 0}(C\delta x)=Cdx}$

${\displaystyle dG=\lim _{\delta x\to 0}(G\delta x)=Gdx}$

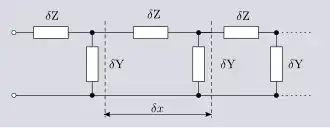
A efectos de análisis, es conveniente agrupar estos elementos en elementos generales de impedancia en serie, Z, y de admitancia en derivación, Y, de forma que;

${\displaystyle dZ=(R+i\omega L)dx=Zdx\,,}$ Y

${\displaystyle dY=(G+i\omega C)dx=Ydx\,.}$

El análisis de esta red (figura 2) arrojará las constantes de línea secundaria: la constante de propagación, 𝛾, (cuyas partes real e imaginaria son la constante de atenuación, 𝛼, y la constante de cambio de fase, 𝛽, respectivamente) y la impedancia característica, 𝑍0, que también, en general, tendrá partes real, 𝑅0, e imaginaria, 𝑋0, lo que hace un total de cuatro constantes secundarias que deben derivarse de las cuatro constantes primarias. El término constante es aún más engañoso para las constantes secundarias, ya que suelen variar bastante con la frecuencia, incluso en una situación ideal en la que las constantes primarias no lo hacen. Esto se debe a que las reactancias del circuito (𝜔𝐿 y 1/(𝜔𝐶)) introducen una dependencia de 𝜔. Es posible elegir valores específicos de las constantes primarias que den como resultado que 𝛼 y 𝑍0 sean independientes de 𝜔 (la condición de Heaviside), pero incluso en este caso, sigue habiendo 𝛽 que es directamente proporcional a 𝜔. Al igual que con las constantes primarias, el significado de "constante" es que las constantes secundarias no varían con la distancia a lo largo de la línea, no que sean independientes de la frecuencia.^[14]​^[15]​^[16]​

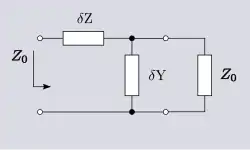
La impedancia característica de una línea de transmisión, 𝑍0, se define como la impedancia que se refleja en una línea infinitamente larga. Una línea de este tipo nunca devolverá una reflexión, ya que la onda incidente nunca llegará al extremo para ser reflejada. Cuando se considera una longitud finita de la línea, el resto de la línea puede ser reemplazado por 𝑍0 como su circuito equivalente. Esto es así porque el resto de la línea sigue siendo infinitamente largo y, por tanto, equivalente a la línea original. Si el segmento finito es muy corto, entonces en el circuito equivalente se modelará mediante una red en L formada por un elemento de 𝑑𝑍 y uno de 𝑑𝑌; el resto viene dado por 𝑍0. Esto da como resultado la red mostrada en la figura 3, que puede analizarse para 𝑍0 utilizando los teoremas habituales de análisis de redes,^[17]​^[18]​

${\displaystyle Z_{0}=\delta Z+{\frac {Z_{0}}{1+Z_{0}\delta Y}}}$

que reordena a,

${\displaystyle {Z_{0}}^{2}-Z_{0}\delta Z={\frac {\delta Z}{\delta Y}}}$

Tomar los límites de ambas partes

${\displaystyle \lim _{\delta x\to 0}({Z_{0}}^{2}-Z_{0}\delta Z)={Z_{0}}^{2}={\frac {dZ}{dY}}}$

y puesto que se suponía que la línea era homogénea longitudinalmente,

${\displaystyle {Z_{0}}^{2}={\frac {Z}{Y}}}$

La relación entre la tensión de entrada de la línea y la tensión a una distancia 𝛿𝑥 mayor de la línea (es decir, después de una sección del circuito equivalente) viene dada por un cálculo estándar del divisor de tensión. El resto de la línea a la derecha, como en el cálculo de la impedancia característica, se sustituye por 𝑍0,^[19]​^[20]​

${\displaystyle {\frac {V_{\mathrm {i} }}{V_{x1}}}={\frac {\delta Z+{\frac {Z_{0}/\delta Y}{Z_{0}+1/\delta Y}}}{\frac {Z_{0}/\delta Y}{Z_{0}+1/\delta Y}}}=1+{\frac {\delta Z}{Z_{0}}}+\delta Z\delta Y}$

Cada sección infinitesimal multiplicará la caída de tensión por el mismo factor. Después de 𝑛 secciones la relación de tensión será,

${\displaystyle {\frac {V_{\mathrm {i} }}{V_{xn}}}=\left(1+{\frac {\delta Z}{Z_{0}}}+\delta Z\delta Y\right)^{n}}$

A una distancia 𝑥 a lo largo de la línea, el número de tramos es 𝑥/𝛿𝑥 de modo que,

${\displaystyle {\frac {V_{\mathrm {i} }}{V_{xn}}}=\left(1+{\frac {\delta Z}{Z_{0}}}+\delta Z\delta Y\right)^{\frac {x}{\delta x}}}$

En el límite como 𝛿𝑥→0,

${\displaystyle {\frac {V_{\mathrm {i} }}{V_{x}}}=\lim _{\delta x\to 0}{\frac {V_{\mathrm {i} }}{V_{xn}}}=\lim _{\delta x\to 0}\left(1+{\frac {\delta Z}{Z_{0}}}+\delta Z\delta Y\right)^{\frac {x}{\delta x}}}$

El término de segundo orden 𝛿𝑍𝛿𝑌 desaparecerá en el límite, por lo que podemos escribir sin pérdida de precisión,

${\displaystyle {\frac {V_{\mathrm {i} }}{V_{x}}}=\lim _{\delta x\to 0}\left(1+{\frac {\delta Z}{Z_{0}}}\right)^{\frac {x}{\delta x}}}$

y comparando con la identidad matemática,

${\displaystyle e^{x}\equiv \lim _{p\to \infty }(1+1/p)^{px}}$

rendimientos,

${\displaystyle V_{\mathrm {i} }=V_{x}e^{{\frac {Z}{Z_{0}}}x}}$

A partir de la definición de constante de propagación,

${\displaystyle V_{\mathrm {i} }=V_{x}e^{\gamma x}\,\!}$

Por lo tanto,

${\displaystyle \gamma ={\frac {Z}{Z_{0}}}={\sqrt {ZY}}}$

Una línea de transmisión ideal no tendrá pérdidas, lo que implica que los elementos resistivos son cero. También da lugar a una impedancia característica puramente real (resistiva). La línea ideal no puede realizarse en la práctica, pero es una aproximación útil en muchas circunstancias. Esto es especialmente cierto, por ejemplo, cuando se utilizan trozos cortos de línea como componentes de circuitos, como los stubs. Una línea corta tiene muy pocas pérdidas, por lo que puede ignorarse y tratarse como una línea ideal. Las constantes secundarias en estas circunstancias son;^[21]​

${\displaystyle \gamma =i\omega {\sqrt {LC}}}$

${\displaystyle \alpha =0\,}$

${\displaystyle \beta =\omega {\sqrt {LC}}}$

${\displaystyle Z_{0}={\sqrt {\frac {L}{C}}}}$

Normalmente, el cable de par trenzado utilizado para frecuencias de audio o velocidades de datos bajas tiene constantes de línea dominadas por R y C. La pérdida dieléctrica suele ser despreciable a estas frecuencias y G es cercana a cero. También ocurre que, a una frecuencia suficientemente baja, 𝑅≫𝜔𝐿 lo que significa que L también puede ignorarse. En esas circunstancias las constantes secundarias pasan a ser,^[22]​

${\displaystyle \gamma \approx {\sqrt {i\omega CR}}}$

${\displaystyle \alpha \approx {\sqrt {\frac {\omega CR}{2}}}}$

${\displaystyle \beta \approx {\sqrt {\frac {\omega CR}{2}}}}$

${\displaystyle Z_{0}\approx {\sqrt {\frac {R}{i\omega C}}}={\sqrt {\frac {R}{2\omega C}}}-i{\sqrt {\frac {R}{2\omega C}}}}$

La atenuación de este tipo de cable aumenta con la frecuencia, provocando la distorsión de las formas de onda. No tan obviamente, la variación de 𝛽 con la frecuencia también causa una distorsión de un tipo llamado dispersión. Para evitar la dispersión, el requisito es que 𝛽 sea directamente proporcional a 𝜔. Sin embargo, en realidad es proporcional a 𝜔 y se produce dispersión. 𝑍0 también varía con la frecuencia y es parcialmente reactiva; ambas características serán la causa de reflexiones desde una terminación de línea resistiva. Este es otro efecto indeseable. La impedancia nominal citada para este tipo de cable es, en este caso, muy nominal, ya que sólo es válida a una frecuencia puntual, normalmente citada a 800 Hz o 1 kHz.^[23]​^[24]​

El cable que funciona a una frecuencia suficientemente alta (radiofrecuencia de onda media o altas velocidades de transmisión de datos) cumplirá las condiciones 𝑅≪𝜔𝐿 y 𝐺≪𝜔𝐶. Esto debe ocurrir finalmente a medida que aumenta la frecuencia para cualquier cable. En esas condiciones, tanto R como G pueden ignorarse (excepto a efectos del cálculo de las pérdidas del cable) y las constantes secundarias pasan a ser;^[25]​

${\displaystyle \gamma \approx i\omega {\sqrt {LC}}}$

${\displaystyle \alpha \approx {\frac {LG+RC}{2{\sqrt {LC}}}}={\tfrac {1}{2}}\left(Z_{0}G+{\frac {R}{Z_{0}}}\right)\approx {\frac {R}{2Z_{0}}}}$

${\displaystyle \beta \approx \omega {\sqrt {LC}}}$

${\displaystyle Z_{0}\approx {\sqrt {\frac {L}{C}}}}$

Las líneas cargadas son líneas diseñadas con una inductancia deliberadamente aumentada. Esto se consigue añadiendo hierro u otro metal magnético al cable o añadiendo bobinas. El objetivo es garantizar que la línea cumpla la condición de Heaviside, que elimina la distorsión causada por la atenuación y la dispersión dependientes de la frecuencia, y asegura que 𝑍0 sea constante y resistiva. Las constantes secundarias se relacionan aquí con las constantes primarias mediante;^[26]​

${\displaystyle \gamma ={\sqrt {RG}}+i\omega {\sqrt {LC}}}$

${\displaystyle \alpha ={\sqrt {RG}}}$

${\displaystyle \beta =\omega {\sqrt {LC}}}$

${\displaystyle Z_{0}={\sqrt {\frac {L}{C}}}={\sqrt {\frac {R}{G}}}}$

La velocidad de propagación viene dada por,

${\displaystyle v=\lambda f.}$

Desde

${\displaystyle \omega =2\pi f}$ y ${\displaystyle \beta ={\frac {2\pi }{\lambda }}}$

entonces,

${\displaystyle v={\frac {\omega }{\beta }}.}$

En los casos en que β puede tomarse como,

${\displaystyle \beta =\omega {\sqrt {LC}}}$

la velocidad de propagación viene dada por,

${\displaystyle v={1 \over {\sqrt {LC}}}.}$

Cuanto menor es la capacitancia, mayor es la velocidad. Con un cable dieléctrico de aire, al que se aproxima con un cable de bajas pérdidas, la velocidad de propagación es muy próxima a c, la velocidad de la luz en el vacío.^[27]​

1. ↑ Connor, p. 8.
2. ↑ Bird, pp. 604–605.
3. ↑ Porges, pp. 223–224.
4. ↑ Bird, pp. 502–503, 519.
5. ↑ "Bulk cable - Category 5 UTP 4-pair PVC", Molex data sheet, 1999, archivado 7/08/2013.
6. ↑ "1583E CAT5E UTP PVC", Belden data sheet 46077, 21 Julio 1999, archivado 7/08/2013.
7. ↑ "CW1308 Internal Telecom Cable" , Eland Cables data sheets, archivado 8/08/2013.
8. ↑ "8281 Coax - Double Braided RG-59/U Type" Belden data sheet, 14 Mayo 2007, archivado 7/08/2013.
9. ↑ "Serial digital video cable", Belden data sheet 1865A, archivado 7/08/2013.
10. ↑ "Suhner coaxial cable", Huber & Suhner data sheet, 24/09/2007, archivado 7/08/2013.
11. ↑ "RG58/U" , General Cable datasheet, pp. 74–76.
12. ↑ "7/8" Cellflex Lite Low-Loss Foam-Dielectric Coaxial Cable", RFS datasheet LCF78-50JFNL, 24 /10/2006, archivado 7/08/2013.
13. ↑ "Trunk cables, paper insulated with aluminium sheath" , Nexus datasheet, archivado 7/08/2013.
14. ↑ ^{a b} Connor, pp. 8–10.
15. ↑ Hickman, p. 113.
16. ↑ Porges, p. 217.
17. ↑ Porges, pp. 216–217.
18. ↑ Connor, pp. 10–11.
19. ↑ Connor, pp. 9–10.
20. ↑ Bird, pp. 609–611.
21. ↑ Connor, p. 17.
22. ↑ Connor, pp. 18–19.
23. ↑ Bird, pp. 612–613.
24. ↑ Porges, p. 219.
25. ↑ Connor, p. 19.
26. ↑ Connor, pp. 19–21.
27. ↑ Connor, pp. 10, 19-20.

• F.R. Connor, Wave Transmission, Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7.
• John Bird, Electrical Circuit Theory and Technology, Newnes, 2007 ISBN 0-7506-8139-X.
• Ian Hickman, Analog Electronics, Newnes, 1999 ISBN 0-7506-4416-8.
• Fred Porges, The Design of Electrical Services for Buildings, Taylor & Francis, 1989 ISBN 0-419-14590-7.