Conjunto de arcos de retroalimentación

En algoritmia y teoría de grafos, un conjunto de arcos de retroalimentación o un conjunto de aristas de retroalimentación en un grafo dirigido es un subconjunto de las aristas del grafo que contiene al menos una arista de cada ciclo del grafo. Eliminar estas aristas del grafo rompe todos los ciclos, produciendo un subgrafo acíclico del grafo dado, a menudo llamado grafo acíclico dirigido. Un conjunto de arcos de retroalimentación con el menor número posible de aristas es un conjunto de arcos de retroalimentación mínimos, y su eliminación deja un subgrafo acíclico máximo. También se utilizan versiones ponderadas de estos problemas de optimización. Si un conjunto de arcos de retroalimentación es mínimo, es decir, si se elimina cualquier arista se obtiene un subconjunto que no es un conjunto de arcos de retroalimentación, entonces tiene una propiedad adicional: invertir todas sus aristas, en lugar de eliminarlas, produce un grafo acíclico dirigido.

Los conjuntos de arcos de retroalimentación tienen aplicaciones en el análisis de circuitos, ingeniería química, resolución de problemas de bloqueo mutuo, voto por orden de preferencia, clasificación de competidores en eventos deportivos, psicología matemática, etología y dibujo de grafos. Encontrar conjuntos de arcos de retroalimentación mínimos y subgrafos acíclicos máximos es NP-difícil; se puede resolver exactamente en tiempo polinómico o en tiempo parametrizado. En tiempo polinómico, el conjunto de arcos de retroalimentación mínimo se puede aproximar mediante un algoritmo de aproximación polilogarítmico, y los subgrafos acíclicos máximos se pueden aproximar dentro de un factor constante. Ambos son difíciles de aproximar más cerca que algún factor constante, un resultado de inaproximabilidad que se puede fortalecer bajo la conjetura del Juego Único. Para torneos en un grafo, el conjunto de arcos de retroalimentación mínimos se puede aproximar con mayor precisión, y para un grafo plano, ambos problemas se pueden resolver con precisión en tiempo polinómico.

Un problema estrechamente relacionado se trata de hallar el conjunto de vértices de retroalimentación, un conjunto de vértices que contiene al menos un vértice de cada ciclo en un grafo dirigido o no dirigido. En grafos, los árboles de expansión son los subgrafos acíclicos más grandes, y el número de aristas eliminadas al formar un árbol de expansión es el rango del circuito.

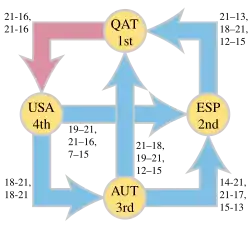
Varios problemas que involucran clasificaciones u ordenamientos pueden resolverse hallando un arco de retroalimentación en el grafo de un torneo, un grafo dirigido con una arista entre cada par de vértices. Invirtiendo las aristas del arco de retroalimentación se obtiene un grafo acíclico dirigido, cuyo único orden topológico puede utilizarse como la clasificación previsible. Entre las aplicaciones de este método se incluyen las siguientes:

• En competiciones deportivas con sistema de todos contra todos, los resultados de cada partido pueden registrarse dirigiendo una arista del perdedor al ganador. Al hallar un arco de retroalimentación mínimo en el grafo resultante, invirtiendo sus aristas y ordenándolo topológicamente, se obtiene una clasificación de todos los competidores. Entre todas las diferentes maneras de elegir una clasificación, esta minimiza el número total de sorpresas, es decir, partidos en los que un competidor de menor rango vence a uno de mayor rango.^[2]​^[3]​^[4]​ Muchos deportes utilizan métodos más sencillos para sistemas de clasificación de torneos de grupo basados en los puntos otorgados por cada partido;^[5]​ estos métodos pueden proporcionar una aproximación constante a la clasificación de mínima sorpresa.^[6]​
• En primatología y, de forma más general, en etología, la jerarquía de dominancias se determinan a menudo buscando un orden con la menor cantidad de reversiones en el comportamiento de dominancia observado, otra forma del problema del conjunto de arco de retroalimentación mínimo.^[7]​^[8]​^[9]​
• En psicología matemática, resulta interesante determinar la clasificación de los sujetos de conjuntos de objetos según un criterio dado, como su preferencia o su percepción del tamaño, basándose en comparaciones por pares entre todos los pares de objetos. El conjunto de arco de retroalimentación mínimo en un gráfico de torneo proporciona una clasificación que discrepa con el menor número posible de resultados por pares.^[2]​^[10]​ Alternativamente, si estas comparaciones resultan en probabilidades independientes para cada ordenamiento por pares, entonces el máxima verosimilitud de la clasificación general puede obtenerse convirtiendo estas probabilidades en log-likelihoods y hallando un arco de retroalimentación de peso mínimo establecido en el torneo resultante.^[2]​^[3]​
• El mismo ordenamiento de máxima verosimilitud puede utilizarse para seriation, el problema en estadística y análisis exploratorio de datos de organizar los elementos en un ordenamiento lineal, en los casos en que se disponga de datos que proporcionen comparaciones por pares entre los elementos.^[3]​^[11]​^[12]​
• En el sistema de voto por orden de preferencia, el método de Kemeny-Young puede describirse como la búsqueda de un ordenamiento que minimice la suma, sobre pares de candidatos, del número de votantes que prefieren el ordenamiento opuesto para ese par.^[13]​ Esto se puede formular y resolver como un problema de conjunto de arcos de retroalimentación de peso mínimo, en el que los vértices representan candidatos, las aristas se dirigen para representar al ganador de cada enfrentamiento directo, y el costo de cada arista representa el número de votantes que se sentirían insatisfechos si se otorgara una clasificación más alta al perdedor del enfrentamiento directo.^[14]​

Otra aplicación temprana de los conjuntos de arcos de retroalimentación se relacionó con el diseño de circuitos secuenciales, en los que las señales pueden propagarse en ciclos a través del circuito en lugar de progresar siempre de las entradas a las salidas. En tales circuitos, un conjunto de arcos de retroalimentación mínimo caracteriza el número de puntos en los que la amplificación es necesaria para permitir que las señales se propaguen sin pérdida de información.^[15]​ En los circuitos síncronos hechos de componentes asíncronos, la sincronización se puede lograr colocando puertas sincronizadas en los bordes de un conjunto de arcos de retroalimentación.^[16]​ Además, cortar un circuito en un conjunto de arcos de retroalimentación reduce el circuito restante a un sistema combinatorio, simplificando su análisis, y el tamaño del conjunto de arcos de retroalimentación controla cuánto análisis adicional se necesita para comprender el comportamiento del circuito a través del corte.^[15]​ De forma similar, en diagramas de flujo de procesos y en ingeniería química, romper las aristas de un diagrama de flujo de proceso en un conjunto de arcos de retroalimentación y adivinar o probar todas las posibilidades de valores en esas aristas permite analizar sistemáticamente el resto del proceso gracias a su aciclicidad. En esta aplicación, la idea de romper aristas de esta manera se denomina desgarro.^[17]​

En dibujo de grafos en capas, los vértices de un grafo dirigido dado se dividen en una secuencia ordenada de subconjuntos (las capas del dibujo), y cada subconjunto se coloca en una línea horizontal de este dibujo, con las aristas extendiéndose hacia arriba y hacia abajo entre estas capas. En este tipo de dibujo, es deseable que la mayoría o la totalidad de las aristas estén orientadas consistentemente hacia abajo, en lugar de mezclarlas, para que las relaciones de alcanzabilidad en el dibujo sean más evidentes. Esto se logra encontrando un conjunto de arcos de retroalimentación mínimo, invirtiendo las aristas de dicho conjunto y seleccionando la partición en capas de forma coherente con el orden topológico del grafo acíclico resultante.^[18]​^[19]​. Los conjuntos de arcos de retroalimentación también se han utilizado para un subproblema diferente del dibujo de grafos en capas: la ordenación de vértices dentro de pares consecutivos de capas.^[20]​.

En la resolución de problemas de bloqueo mutuo en un sistema operativo, el problema de eliminar el menor número de dependencias para romper un bloqueo mutuo puede modelarse como el de encontrar un conjunto mínimo de arcos de retroalimentación.^[21]​^[22]​ Sin embargo, debido a la dificultad computacional para encontrar este conjunto y a la necesidad de velocidad en los componentes del sistema operativo, en esta aplicación se suelen utilizar procedimientos heurísticos en lugar de algoritmos exactos.^[22]​

El conjunto de arcos de retroalimentación mínimo y el subgrafo acíclico máximo son equivalentes a efectos de optimización exacta, ya que uno es el complemento del otro. Sin embargo, en cuanto a la complejidad parametrizada y a la aproximación, difieren, ya que el análisis utilizado para estos tipos de algoritmos depende del tamaño de la solución y no solo del tamaño del grafo de entrada, y el conjunto de arcos de retroalimentación mínimos y el subgrafo acíclico máximo tienen tamaños diferentes.^[23]​

Un conjunto de arcos de retroalimentación de un grafo dado ${\displaystyle G}$ es el mismo que un conjunto de vértices de retroalimentación de un grafo lineal dirigido de ${\displaystyle G}$. Aquí, un conjunto de vértices de retroalimentación se define de forma análoga a un conjunto de arcos de retroalimentación, como un subconjunto de los vértices del grafo cuya supresión eliminaría todos los ciclos. El grafo lineal de un grafo dirigido ${\displaystyle G}$ tiene un vértice para cada arista de ${\displaystyle G}$, y una arista para cada camino de dos aristas en ${\displaystyle G}$. En la otra dirección, el conjunto de vértices de retroalimentación mínimo de un grafo dado ${\displaystyle G}$ puede obtenerse a partir de la solución de un problema de conjunto de arcos de retroalimentación mínimos en un grafo obtenido al dividir cada vértice de ${\displaystyle G}$ en dos vértices, uno para las aristas entrantes y otro para las aristas salientes. Estas transformaciones permiten obtener algoritmos exactos para conjuntos de arcos de retroalimentación y para conjuntos de vértices de retroalimentación que se convertirán entre sí, con una traslación apropiada de sus límites de complejidad. Sin embargo, esta transformación no preserva la calidad de aproximación para el problema del subgrafo acíclico máximo.^[21]​^[24]​

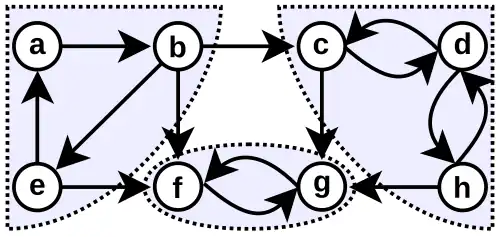
Tanto en soluciones exactas como aproximadas del problema del conjunto de arcos de retroalimentación, basta con resolver por separado cada componente fuertemente conexo del grafo dado y descomponerlos aún más hasta obtener sus componentes biconectados, dividiéndolos en los vértices de articulación. La elección de la solución dentro de cualquiera de estos subproblemas no afecta a los demás, y las aristas que no aparecen en ninguno de estos componentes son inútiles para su inclusión en el conjunto de arcos de retroalimentación.^[25]​ Cuando uno de estos componentes puede separarse en dos subgrafos inconexos eliminando dos vértices, se aplica una descomposición más compleja, que permite dividir el problema en subproblemas derivados de los componentes triconectados de sus componentes fuertemente conexos.^[26]​

Una forma de encontrar el conjunto mínimo de arcos de retroalimentación es buscar un orden de vértices tal que la menor cantidad posible de aristas se dirijan desde vértices posteriores a vértices anteriores en el orden.^[27]​ Buscar todos las permutaciones de un grafo de ${\displaystyle n}$-vértices requeriría un tiempo ${\displaystyle O(n!)}$, pero un método de programación dinámica basado en el algoritmo de Held-Karp puede encontrar la permutación óptima en tiempo ${\displaystyle O(n2^{n})}$, utilizando también una cantidad exponencial de espacio de memoria.^[28]​^[29]​ Un algoritmo divide y vencerás que prueba todas las particiones de los vértices en dos subconjuntos iguales y recurre dentro de cada subconjunto, puede resolver el problema en tiempo ${\displaystyle O(4^{n}/{\sqrt {n}})}$, utilizando pSPACE.^[29]​

En complejidad parametrizada, el tiempo de los algoritmos se mide no solo en términos del tamaño del grafo de entrada, sino también en términos de un parámetro independiente del grafo. En particular, para el problema del conjunto mínimo de arcos de retroalimentación, el llamado parámetro natural es el tamaño del conjunto mínimo de arcos de retroalimentación. En gráficos con ${\displaystyle n}$ vértices, con parámetro natural ${\displaystyle k}$, el problema del conjunto de arcos de retroalimentación se puede resolver en tiempo ${\displaystyle O(n^{4}4^{k}k^{3}k!)}$, transformándolo en un problema de conjunto de vértices de retroalimentación equivalente y aplicación de un algoritmo de conjunto de vértices de retroalimentación parametrizado. Dado que el exponente de ${\displaystyle n}$ en este algoritmo es la constante ${\displaystyle 4}$, independiente de ${\displaystyle k}$, se dice que este algoritmo es manejable con parámetros fijos.^[30]​

También se han estudiado otros parámetros además del parámetro natural. Un algoritmo manejable con parámetros fijos mediante programación dinámica puede encontrar conjuntos de arcos de retroalimentación mínimos en tiempo ${\displaystyle O(2^{r}m^{4}\log m)}$, donde ${\displaystyle r}$ es el rango de un circuito del grafo no dirigido subyacente. El rango del circuito es un análogo no dirigido del conjunto de arcos de retroalimentación, el número mínimo de aristas que deben eliminarse de un grafo conexo para reducirlo a un árbol de expansión. Es mucho más fácil de calcular que el conjunto de arcos de retroalimentación mínimos.^[24]​ Para grafos de anchura de árbol ${\displaystyle t}$, la programación dinámica en una descomposición de árbol del grafo puede encontrar el conjunto de arcos de retroalimentación mínimos en tiempo polinómico en respecto al tamaño del grafo y exponencial respecto a ${\displaystyle O(t\log t)}$. Bajo la hipótesis del tiempo exponencial, no es posible obtener una dependencia más favorable de ${\displaystyle t}$.^[31]​

En lugar de minimizar el tamaño del conjunto de arcos de retroalimentación, los investigadores también han buscado minimizar el número máximo de aristas eliminadas de cualquier vértice. Esta variación del problema se puede resolver en tiempo polinómico.^[32]​ Todos los conjuntos de arcos de retroalimentación mínimos se pueden listar mediante un algoritmo con retardo polinómico por conjunto.^[33]​

Problemas no resueltos de la matemática: ¿El problema del conjunto de arcos de retroalimentación tiene un algoritmo de aproximación con una relación de aproximación constante?

El algoritmo de aproximación de tiempo polinómico más conocido para el conjunto de arcos de retroalimentación tiene el valor no constante ${\displaystyle O(\log n\log \log n)}$. Esto significa que el tamaño del conjunto de arcos de retroalimentación que encuentra es, como máximo, mayor que el óptimo en este factor.^[21]​ Determinar si el conjunto de arcos de retroalimentación tiene un algoritmo de aproximación de razón constante o si es necesaria una razón no constante sigue siendo un problema abierto.^[34]​

El problema del subgrafo acíclico máximo tiene un algoritmo de aproximación sencillo que logra una razón de aproximación de ${\displaystyle {\tfrac {1}{2}}}$:

• Fijar un orden arbitrario de los vértices.
• Dividir las aristas en dos subgrafos acíclicos: uno con las aristas dirigidas de forma coherente con el ordenamiento y el otro con las aristas dirigidas de forma opuesta.
• Devolver el mayor de los dos subgrafos.

Esto se puede mejorar usando un algoritmo voraz para elegir el orden. Este algoritmo encuentra y elimina un vértice con el mayor número de aristas entrantes y salientes posible, ordena recursivamente el grafo restante y, a continuación, coloca el vértice eliminado en un extremo del orden resultante. Para grafos con ${\displaystyle m}$ aristas y ${\displaystyle n}$ vértices, esto produce un subgrafo acíclico con ${\displaystyle m/2+n/6}$ aristas, en tiempo lineal, lo que da una razón de aproximación de ${\displaystyle {\tfrac {1}{2}}+\Omega (n/m)}$.^[35]​ Otro algoritmo de aproximación en tiempo polinómico, más complejo, se aplica a grafos con un grado máximo ${\displaystyle \Delta }$, y encuentra un subgrafo acíclico con ${\displaystyle m/2+\Omega (m/{\sqrt {\Delta }})}$ aristas, lo que da una razón de aproximación para ${\displaystyle {\tfrac {1}{2}}+\Omega (1/{\sqrt {\Delta }})}$.^[36]​^[37]​ Cuando ${\displaystyle \Delta =3}$, se puede alcanzar la razón de aproximación ${\displaystyle 8/9}$.^[38]​

En grafos planos dirigidos, el problema del conjunto de arcos de retroalimentación es dual al problema de contraer un conjunto de aristas (un dijoin) para hacer el grafo resultante fuertemente conexo.^[39]​ Este problema dual es resoluble polinómicamente,^[40]​ y por lo tanto el problema del conjunto de arcos de retroalimentación mínimo plano también lo es.^[41]​^[40]​ Se puede resolver en tiempo ${\displaystyle O(n^{5/2}\log n)}$.^[42]​ Una versión ponderada del problema se puede resolver en tiempo ${\displaystyle O(n^{3})}$,^[39]​ o cuando los pesos son enteros positivos que son como máximo un número ${\displaystyle N}$, en tiempo ${\displaystyle O(n^{5/2}\log nN)}$.^[42]​ Estos algoritmos planos se pueden extender a los grafos que no presentan el problema de los tres servicios ${\displaystyle K_{3,3}}$ como menor del grafo, usando el hecho de que los componentes triconectados de estos grafos son planos o de tamaño acotado.^[26]​ Los grafos planos también se han generalizado de forma diferente a una clase de grafos dirigidos denominados dígrafos débilmente acíclicos, definidos por la integrabilidad de un determinado politopo asociado con sus conjuntos de arcos de retroalimentación. Todo grafo dirigido planar es débilmente acíclico en este sentido, y el problema del conjunto de arcos de retroalimentación puede resolverse en tiempo polinómico para todos los dígrafos débilmente acíclicos.^[43]​

Los grafos de flujo reducibles son otra clase de grafos dirigidos en los que el problema del conjunto de arcos de retroalimentación se puede resolver en tiempo polinómico. Estos grafos describen el flujo de control en programas estructurados para muchos lenguajes de programación. Aunque los programas estructurados suelen producir grafos de flujo dirigidos planos, la definición de reducibilidad no exige que el grafo sea plano.^[44]​

Cuando el problema del conjunto de arcos de retroalimentación mínimos se limita a torneos, tiene un esquema de aproximación de tiempo polinómico, que se generaliza a una versión ponderada del problema.^[45]​ También se conoce un algoritmo parametrizado subexponencial para conjuntos de arcos de retroalimentación ponderados en torneos.^[14]​ El problema del subgrafo acíclico máximo para un grafo denso también tiene un esquema de aproximación de tiempo polinómico. Sus ideas principales son aplicar un redondeo aleatorio a una relajación de programación lineal del problema y, a deshacer el proceso aleatorio del algoritmo resultante mediante los caminos en un grafo expansor.^[34]​^[46]​

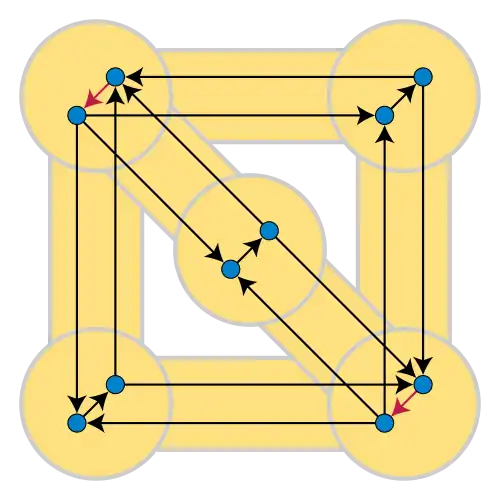
Para aplicar la teoría de NP-completo al conjunto de arcos de retroalimentación mínimos, es necesario modificar el problema para que pase de ser un problema de optimización (cuántas aristas se pueden eliminar para romper todos los ciclos) a un problema de decisión equivalente, con una respuesta de sí o no (si es posible o no eliminar ${\displaystyle k}$ aristas). Por lo tanto, la versión de decisión del problema del conjunto de arco de retroalimentación toma como entrada tanto un grafo dirigido como un número ${\displaystyle k}$. Pregunta si todos los ciclos se pueden romper eliminando como máximo ${\displaystyle k}$ aristas, o equivalentemente si hay un subgrafo acíclico con al menos ${\displaystyle |E(G)|-k}$ aristas. Este problema es NP-completo, lo que implica que no se espera que ni este ni el problema de optimización tengan algoritmos de tiempo polinómico. Era uno de los conjuntos originales de Richard Karp de sus 21 problemas NP-completos. Su NP-completitud fue demostrada por Karp y Eugene Lawler al mostrar que las entradas para otro problema complejo, la cobertura de vértices, podían transformarse (reducirse) en entradas equivalentes al problema de decisión del conjunto de arcos de retroalimentación.^[47]​^[48]​

Algunos problemas NP-completos pueden resultar más fáciles cuando sus entradas se restringen a casos especiales. Pero para el caso especial más importante del problema del conjunto de arcos de retroalimentación, el caso de los torneos, el problema sigue siendo NP-completo.^[49]​^[50]​

La clase de complejidad APX se define como compuesta por problemas de optimización que tienen un algoritmo de aproximación de tiempo polinómico que logra un algoritmo de aproximación constante. Aunque se desconocen dichas aproximaciones para el problema del conjunto de arcos de retroalimentación, se sabe que el problema es APX-difícil, lo que significa que se podrían usar aproximaciones precisas para lograr aproximaciones igualmente precisas para todos los demás problemas en APX. Como consecuencia de su prueba de dificultad, a excepción de P= NP, no tiene una razón de aproximación de tiempo polinómico mejor que 1,3606. Este es el mismo umbral de dificultad de aproximación que se conoce para la cobertura de vértices, y la prueba utiliza la reducción de Karp-Lawler desde la cobertura de vértices hasta el conjunto de arcos de retroalimentación, lo que preserva la calidad de las aproximaciones.^[34]​^[51]​^[52]​^[53]​ Mediante una reducción diferente, el problema del subgrafo acíclico máximo también es APX-difícil y NP-difícil para aproximarse con una precisión de 65/66 respecto al óptimo.^[38]​

La dificultad de aproximación de estos problemas también se ha estudiado con supuestos de dificultad computacional no probados, que son estándar en la teoría de la complejidad computacional, pero más robustos que P ≠ NP. Si la conjetura del Juego Único es verdadera, entonces el problema del conjunto de arco de retroalimentación mínimo es difícil de aproximar en tiempo polinómico dentro de cualquier factor constante, y el problema del conjunto de arco de retroalimentación máximo es difícil de aproximar dentro de un factor de ${\displaystyle {\tfrac {1}{2}}+\varepsilon }$, para cad ${\displaystyle \varepsilon >0}$.^[54]​ Más allá del tiempo polinómico para algoritmos de aproximación, si la hipótesis de tiempo exponencial es verdadera, entonces para cada ${\displaystyle \varepsilon >0}$ el conjunto de arco de retroalimentación mínimo no tiene una aproximación dentro de un factor ${\displaystyle {\tfrac {7}{6}}-\varepsilon }$ que pueda calcularse en el límite de tiempo subexponencial ${\displaystyle O(2^{n^{1-\varepsilon }})}$.^[55]​

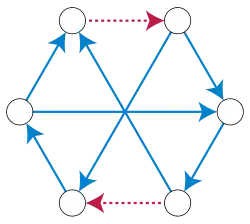
En grafos dirigidos planos, el problema del conjunto de arcos de retroalimentación obedece a un teorema minimax: el tamaño mínimo de un conjunto de arcos de retroalimentación es igual al número máximo de ciclos dirigidos con aristas disjuntas que se pueden encontrar en el grafo.^[41]​^[56]​ Esto no se cumple para otros grafos. Por ejemplo, la primera ilustración muestra una versión dirigida del grafo no plano ${\displaystyle K_{3,3}}$, en la que el tamaño mínimo de un conjunto de arcos de retroalimentación es dos, mientras que el número máximo de ciclos dirigidos con aristas disjuntas es solo uno.

Todo grafo de torneo tiene un camino hamiltoniano, y las trayectorias hamiltonianas se corresponden exactamente con los conjuntos de arcos de retroalimentación mínimos, disjuntos de la trayectoria correspondiente. La trayectoria hamiltoniana para un conjunto de arcos de retroalimentación se obtiene invirtiendo sus arcos y hallando un orden topológico del torneo acíclico resultante. Cada par consecutivo del orden debe ser disjunto de los conjuntos de arcos de retroalimentación, ya que, de lo contrario, se podría encontrar un conjunto de arcos de retroalimentación más pequeño invirtiendo ese par. Por lo tanto, este orden da un camino a través de arcos del torneo original, cubriendo todos los vértices. Por el contrario, de cualquier camino hamiltoniano, el conjunto de aristas que conectan vértices posteriores en el camino con los anteriores forma un conjunto de arco de retroalimentación. Es mínimo, porque cada una de sus aristas pertenece a un ciclo con las aristas del camino hamiltoniano que es disjunto de todos los demás ciclos de este tipo.^[57]​ En un torneo, puede darse el caso de que el conjunto de arcos de retroalimentación mínimo y el subgrafo acíclico máximo estén ambos cerca de la mitad de las aristas. Más precisamente, cada grafo de torneo tiene un conjunto de arcos de retroalimentación de tamaño ${\displaystyle {\tbinom {n}{2}}/2-\Omega (n^{3/2})}$, y algunos torneos requieren tamaño ${\displaystyle {\tbinom {n}{2}}/2-O(n^{3/2})}$.^[58]​ Para casi todos los torneos, el tamaño es de al menos ${\displaystyle {\tbinom {n}{2}}/2-1.73n^{3/2}}$.^[59]​ Cada grafo acíclico dirigido ${\displaystyle D}$ puede ser incrustado como un subgrafo de un grafo de torneo más grande, de tal manera que ${\displaystyle D}$ sea el único conjunto de arco de retroalimentación mínimo del torneo. El tamaño de este torneo se ha definido como el número de inversión of ${\displaystyle D}$, y, entre grafos acíclicos dirigidos con el mismo número de vértices, es mayor cuando ${\displaystyle D}$ es en sí mismo un torneo (acíclico).^[60]​^[61]​

Un grafo dirigido tiene una vuelta de Euler siempre que sea fuertemente conexo y cada vértice tenga el mismo número de aristas entrantes y salientes. Para un grafo de este tipo, con ${\displaystyle m}$ aristas y ${\displaystyle n}$ vértices, el tamaño mínimo de un conjunto de arcos de retroalimentación es siempre al menos ${\displaystyle (m^{2}+mn)/2n^{2}}$. Hay infinitos grafos dirigidos eulerianos para los que esta cota es ajustada.^[62]​ Si un grafo dirigido tiene ${\displaystyle n}$ vértices, con un máximo de tres aristas por vértice, entonces tiene un conjunto de arcos de retroalimentación de un máximo de ${\displaystyle n/3}$ aristas, y algunos grafos requieren este número. Si un grafo dirigido tiene ${\displaystyle m}$ aristas, con un máximo de cuatro aristas por vértice, entonces tiene un conjunto de arcos de retroalimentación de un máximo de ${\displaystyle m/3}$ aristas, y algunos grafos requieren este número.^[63]​