Conjetura de Hadwiger (geometría combinatoria)

Problemas no resueltos de la matemática: ¿Puede cualquier cuerpo convexo de ${\displaystyle n}$ dimensiones ser cubierto por ${\displaystyle 2^{n}}$ copias más pequeñas de sí mismo?

En geometría discreta, la conjetura de Hadwiger establece que cualquier cuerpo convexo en un espacio euclídeo de dimensión n puede ser cubierto por 2ⁿ o menos cuerpos menores homotéticos con respecto al cuerpo original, y que, además, la cota superior de 2ⁿ es necesaria si y solo si el cuerpo es un paralelepípedo. También existe una formulación equivalente en términos del número de focos necesarios para iluminar el cuerpo.

La conjetura de Hadwiger recibe su nombre de Hugo Hadwiger, quien la incluyó en una lista de problemas sin resolver en 1957. Sin embargo, fue estudiada previamente por Levi (1955) e, independientemente, por Gohberg y Markus (1960). Además, existe una conjetura de Hadwiger diferente relacionada con la coloración de grafos, y en algunas fuentes, la conjetura geométrica de Hadwiger también se denomina «conjetura de Levi-Hadwiger» o «problema de recubrimiento de Hadwiger-Levi».

La conjetura permanece sin resolver incluso en tres dimensiones, aunque el caso bidimensional fue resuelto por Levi (1955).

Formalmente, la conjetura de Hadwiger es: Si K es cualquier cuerpo convexo acotado definido en el espacio euclídeo Rⁿ n-dimensional, entonces existe un conjunto de 2ⁿ escalares s_i y un conjunto de 2ⁿ vectores de traslación v_i tales que todos los s_i están en el rango 0 < s_i < 1, y

${\displaystyle K\subseteq \bigcup _{i=1}^{2^{n}}s_{i}K+v_{i}.}$

Además, la cota superior es necesaria si y solo si K es un paralelepípedo, en cuyo caso todos los 2ⁿ escalares pueden elegirse iguales a 1/2.

Como demostró Vladímir Boltianski, la cuestión es equivalente al problema de la iluminación: ¿cuántos focos deben colocarse fuera de un cuerpo convexo opaco para iluminar completamente su exterior? Para este problema, un cuerpo solo se considera iluminado si, por cada punto de su contorno, hay al menos un foco separado del cuerpo para todas las tangentes que lo intersecan en ese punto; por lo tanto, aunque las caras de un cubo solo puedan estar iluminadas por dos focos, los planos tangentes a sus vértices y aristas hacen que se necesiten muchas más luces para estar completamente iluminado. Para cualquier cuerpo convexo, el número de focos necesarios para iluminarlo completamente resulta ser igual al número de copias más pequeñas del cuerpo necesarias para cubrirlo.^[1]​

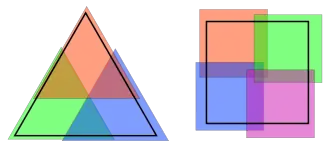
Como se muestra en la ilustración, un triángulo puede estar cubierto por tres copias más pequeñas de sí mismo y, de forma más general, en cualquier dimensión, un símplex puede estar cubierto por n + 1 copias de sí mismo, escaladas por un factor de n/(n + 1). Sin embargo, cubrir un cuadrado con cuadrados más pequeños (con lados paralelos al original) requiere cuatro cuadrados más pequeños, ya que cada uno puede cubrir solo uno de los cuatro vértices del cuadrado mayor. En dimensiones superiores, cubrir un hipercubo, o de forma más general, un paralelepípedo con copias homotéticas más pequeñas de la misma forma, requiere una copia separada para cada vértice del hipercubo o paralelepípedo original. Dado que estas formas tienen 2ⁿ vértices, se necesitan 2ⁿ copias más pequeñas. Este número también es suficiente: un cubo o paralelepípedo puede estar cubierto por 2ⁿ copias, escaladas por un factor de 1/2. La conjetura de Hadwiger plantea que los paralelepípedos constituyen el peor caso para este problema, y que cualquier otro cuerpo convexo puede estar cubierto por menos de 2ⁿ copias más pequeñas de sí mismo.^[1]​

El caso bidimensional fue resuelto por Levi (1955): todo conjunto convexo acotado bidimensional puede estar cubierto por cuatro copias más pequeñas de sí mismo, siendo la cuarta copia necesaria solo en el caso de los paralelogramos. Sin embargo, la conjetura permanece abierta en dimensiones superiores, salvo en algunos casos especiales. El límite superior asintótico más conocido para el número de copias más pequeñas necesarias para cubrir un cuerpo dado es:^[2]​

${\displaystyle \displaystyle 4^{n}\exp {\frac {-cn}{\log ^{8}n}}}$

donde ${\displaystyle c}$ es una constante positiva. Para ${\displaystyle n}$ pequeños, el límite superior de ${\displaystyle (n+1)n^{n-1}-(n-1)(n-2)^{n-1}}$ establecido por Lassak (1988) es mejor que el asintótico. En tres dimensiones se sabe que 16 copias siempre son suficientes, pero esto aún dista mucho del límite conjeturado de 8 copias.^[1]​

Se sabe que la conjetura es válida para ciertas clases especiales de cuerpos convexos, incluyendo, en dimensión tres, los poliedros con simetría central y los cuerpos de espesor constante.^[1]​ El número de copias necesarias para cubrir cualquier zonoedro (excepto un paralelepípedo) es como máximo ${\displaystyle (3/4)2^{n}}$, mientras que para cuerpos con una superficie lisa (es decir, con un solo plano tangente por punto límite), se necesitan como máximo ${\displaystyle n+1}$ copias más pequeñas para cubrir el cuerpo, como ya se demostró con Levi.^[1]​

• Conjetura de Borsuk sobre la cobertura de cuerpos convexos con conjuntos de menor diámetro.

• Boltjansky, Vladimir G.; Gohberg, Israel (1985). «11. Hadwiger's Conjecture». Results and Problems in Combinatorial Geometry. Cambridge: Cambridge University Press. pp. 44-46. ISBN 978-0-521-26923-0. .
• Brass, Peter; Moser, William; Pach, János (2005). «3.3 Levi–Hadwiger Covering Problem and Illumination». Research Problems in Discrete Geometry. Springer-Verlag. pp. 136-142. ISBN 978-0-387-23815-9. .
• Campos, Marcelo; van Hintum, Peter; Morris, Robert; Tiba, Marius (2023), «Towards Hadwiger's Conjecture via Bourgain Slicing», International Mathematics Research Notices 2024 (10): 8282-8295, arXiv:2206.11227, doi:10.1093/imrn/rnad198 ..
• Gohberg, Israel Ts.; Markus, Alexander S. (1960), «A certain problem about the covering of convex sets with homothetic ones», Izvestiya Moldavskogo Filiala Akademii Nauk SSSR (en russian) 10 (76): 87-90 ..
• Hadwiger, Hugo (1957), «Ungelöste Probleme Nr. 20», Elemente der Mathematik 12: 121 ..
• Huang, Han; Slomka, Boaz A.; Tkocz, Tomasz; Vritsiou, Beatrice-Helen (2022), «Improved bounds for Hadwiger's covering problem via thin-shell estimates», Journal of the European Mathematical Society (en inglés) 24 (4): 1431-1448, ISSN 1435-9855, arXiv:1811.12548, doi:10.4171/jems/1132 ..
• Lassak, Marek (1988), «Covering the boundary of a convex set by tiles», Proceedings of the American Mathematical Society 104 (1): 269-272, MR 0958081, doi:10.1090/s0002-9939-1988-0958081-7 ..
• Levi, Friedrich Wilhelm (1955), «Überdeckung eines Eibereiches durch Parallelverschiebungen seines offenen Kerns», Archiv der Mathematik 6 (5): 369-370, S2CID 121459171, doi:10.1007/BF01900507 ..