Condensación capilar

En ciencia de los materiales y biología, la condensación capilar es el «proceso por el cual la adsorción multicapa del vapor [fase] en un medio poroso continúa hasta el punto en que los espacios porosos se llenan con líquido condensado a partir del vapor [fase].»^[1]​ El aspecto único de la condensación capilar es que la condensación del vapor se produce por debajo de la presión de vapor de saturación, P_sat, del líquido puro.^[2]​ Este resultado se debe al aumento del número de interacciones van der Waals entre las moléculas en fase vapor dentro del espacio confinado de un capilar. Una vez que se ha producido la condensación, se forma inmediatamente un menisco en la interfaz líquido-vapor, lo que permite el equilibrio por debajo de la presión de vapor de saturación. La formación del menisco depende de la tensión superficial del líquido y de la forma del capilar, como muestra la Ecuación de Young-Laplace. Al igual que con cualquier interfaz líquido-vapor que implique un menisco, la ecuación de Kelvin proporciona una relación entre la presión de vapor en equilibrio y la presión de vapor de saturación.^[3]​^[4]​^[5]​^[6]​ Un capilar no tiene por qué ser necesariamente una forma tubular cerrada, sino que puede ser cualquier espacio confinado con respecto a su entorno.

La condensación capilar es un factor importante tanto en estructuras porosas naturales como sintéticas. En estas estructuras, los científicos utilizan el concepto de condensación capilar para determinar la distribución del tamaño de los poros y la superficie mediante isotermas de adsorción.^[3]​^[4]​^[5]​^[6]​ Las aplicaciones sintéticas, como la sinterización^[7]​ de materiales también dependen en gran medida de los efectos puente resultantes de la condensación capilar. En contraste con las ventajas de la condensación capilar, también puede causar muchos problemas en aplicaciones de la ciencia de los materiales, como la microscopía de fuerza atómica^[8]​ y los sistemas microelectromecánicos.^[9]​

La ecuación de Kelvin puede utilizarse para describir el fenómeno de la condensación capilar debido a la presencia de un menisco curvo. ^[2]​

${\displaystyle \ln {\frac {P_{v}}{P_{sat}}}=-{\frac {2H\gamma V_{l}}{RT}}\ }$

Donde...

${\displaystyle \ P_{v}}$ = presión de vapor en equilibrio

${\displaystyle \ P_{sat}}$ = presión de vapor de saturación

${\displaystyle \ H}$ = curvatura media del menisco

${\displaystyle \ \gamma }$ = tensión superficial líquido/vapor

${\displaystyle \ V_{l}}$ = volumen molar del líquido

${\displaystyle \ R}$ = constante de los gases ideales

${\displaystyle \ T}$ = temperatura

Esta ecuación, que se muestra arriba, rige todos los sistemas de equilibrio que involucran menisco y proporciona un razonamiento matemático para el hecho de que la condensación de una especie determinada se produce por debajo de la presión de vapor de saturación (P_v < P_sat) dentro de un capilar. En el núcleo de la ecuación de Kelvin se encuentra la diferencia de presión entre las fases líquida y gaseosa, lo que contrasta con los diagramas de fase tradicionales, en los que el equilibrio de fase se produce a una sola presión, conocida como P_sat, para una temperatura dada. Esta caída de presión (${\displaystyle \scriptstyle \Delta P}$) se debe únicamente a la tensión superficial líquido/vapor y a la curvatura del menisco, tal y como se describe en la ecuación de Young-Laplace.^[2]​

${\displaystyle \ \Delta P=2H\gamma }$

En la ecuación de Kelvin, la presión de vapor de saturación, la tensión superficial y el volumen molar son propiedades inherentes a las especies en equilibrio y se consideran constantes con respecto al sistema. La temperatura también es una constante en la ecuación de Kelvin, ya que es una función de la presión de vapor de saturación y viceversa. Por lo tanto, las variables que más influyen en la condensación capilar son la presión de vapor de equilibrio y la curvatura media del menisco.

La relación entre la presión de vapor de equilibrio y la presión de vapor de saturación puede considerarse como una medida de la humedad relativa de la atmósfera. A medida que Pv/Psat aumenta, el vapor seguirá condensándose dentro de un capilar determinado. Si P_v/P_sat disminuye, el líquido comenzará a evaporarse a la atmósfera en forma de moléculas de vapor.^[2]​ La siguiente figura muestra cuatro sistemas diferentes en los que P_v/P_sat aumenta de izquierda a derecha.

Figura 2: Cuatro sistemas capilares diferentes con P_v creciente de A a D.

Sistema A → P_v=0, no hay vapor presente en el sistema

Sistema B → P_v=P₁<P_sat, se produce condensación capilar y se alcanza el equilibrio entre el líquido y el vapor.

Sistema C → P_v=P₂<P_sat, P₁<P₂, a medida que aumenta la presión de vapor, la condensación continúa para satisfacer la ecuación de Kelvin

Sistema D → P_v=P_max<P_sat, la presión de vapor aumenta hasta su valor máximo permitido y el poro se llena por completo

La ecuación de Kelvin indica que, a medida que P_v/P_sat aumenta dentro de un capilar, el radio de curvatura también aumenta, creando una interfaz más plana. (Nota: esto no significa que un radio de curvatura mayor provoque una mayor condensación de vapor. Véase la discusión sobre el ángulo de contacto más adelante). La figura 2 anterior muestra esta dependencia en una situación sencilla en la que el radio capilar se expande hacia la abertura del capilar y, por lo tanto, la condensación de vapor se produce de forma suave en un rango de presiones de vapor. En una situación paralela, en la que el radio capilar es constante a lo largo de su altura, la condensación de vapor se produciría mucho más rápidamente, alcanzando el radio de curvatura de equilibrio (radio de Kelvin) lo más rápido posible.^[2]​ Esta dependencia de la geometría de los poros y la curvatura puede dar lugar a histéresis y a equilibrios líquido/vapor muy diferentes en rangos de presión muy pequeños.

También cabe mencionar que las diferentes geometrías de los poros dan lugar a diferentes tipos de curvatura. En los estudios científicos sobre la condensación capilar, la situación del menisco hemisférico (el que resulta de un poro perfectamente cilíndrico) es la más investigada debido a su simplicidad.^[5]​ Los meniscos cilíndricos también son sistemas útiles porque suelen ser el resultado de arañazos, cortes y capilares tipo hendidura en las superficies. Hay muchos otros tipos de curvatura posibles y se pueden encontrar fácilmente ecuaciones para la curvatura de los meniscos en numerosas fuentes.^[5]​^[10]​ A continuación se muestran las ecuaciones para los meniscos hemisféricos y cilíndricos.

Ecuación general de la curvatura:

${\displaystyle \ H={\frac {1}{2}}({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}})}$

Cilindro: ${\displaystyle \ R_{1}=r}$ ${\displaystyle \ R_{2}=\infty }$

${\displaystyle \ H={\frac {1}{2r}}}$

Hemisferio: ${\displaystyle \ R_{1}=r}$ ${\displaystyle \ R_{2}=r}$

${\displaystyle \ H={\frac {1}{r}}}$

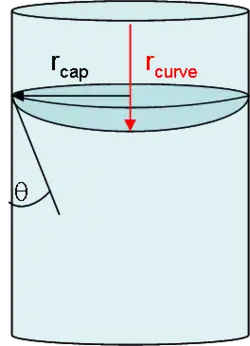
El ángulo de contacto, o ángulo de contacto, es un parámetro muy importante en sistemas reales en los que rara vez se consigue una humectación perfecta (${\displaystyle \ \theta }$ = 0^o). La ecuación de Young proporciona una explicación de la implicación del ángulo de contacto en la condensación capilar. La ecuación de Young explica que la tensión superficial entre las fases líquida y gaseosa se escala al coseno del ángulo de contacto. Como se muestra en la figura de la derecha, el ángulo de contacto entre un líquido condensado y la pared interior de un capilar puede afectar en gran medida al radio de curvatura. Por esta razón, el ángulo de contacto está intrínsecamente ligado al término de curvatura de la ecuación de Kelvin. A medida que aumenta el ángulo de contacto, también aumenta el radio de curvatura. Esto significa que un sistema con humectación perfecta presentará una mayor cantidad de líquido en sus poros que un sistema con humectación imperfecta (${\displaystyle \ \theta }$ > 0^o). Además, en sistemas donde ${\displaystyle \ \theta }$ = 0^o, el radio de curvatura es igual al radio capilar. ^[2]​ Debido a estas complicaciones causadas por el ángulo de contacto, los estudios científicos suelen diseñarse asumiendo ${\displaystyle \ \theta }$ = 0^o.^[3]​^[4]​^[5]​^[6]​