Circunferencias ortogonales
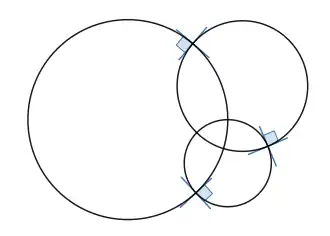
En geometría, se dice que dos circunferencias son ortogonales si sus respectivas rectas tangentes en los puntos de intersección son perpendiculares (es decir, se intersecan formando un ángulo recto).[1]
Una línea recta que pasa por el centro de una círcnferencia es ortogonal a este, y si las líneas rectas también se consideran un tipo de circunferencia generalizada, por ejemplo, en la geometría inversiva, entonces un par de líneas rectas ortogonales, o una circunferencia y una línea recta que pasa por su centro, son circunferencias generalizadas ortogonales entre sí.
En el modelo del disco conforme de la geometría hiperbólica, cada línea geodésica es un arco de una circunferencia generalizada ortogonal a la circunferencia del punto ideal que delimita el disco.
Propiedades
En geometría, se dice que dos circunferencias que se intersecan en un plano son ortogonales si en cada uno de los dos puntos de intersección las tangentes con una y con la otra circunferencia son ortogonales. Por razones de simetría, basta con que la propiedad anterior se dé en uno de los dos puntos de intersección. Por otra parte, cada una de las tangentes antes mencionadas a una de las circunferencias pasa por el centro de la otra.

La figura formada por los dos centros O, O´ y uno de los dos puntos de intersección es un triángulo rectángulo. Por el teorema de Pitágoras, resulta la relación entre los dos radios y la distancia entre los centros: OO' 2 = R 2 + R' 2.
Por el contrario, si dos circunferencias se intersecan y verifican esta relación, entonces son ortogonales entre sí.
Para que dos circunferencias sean ortogonales es necesario y suficiente que exista un diámetro de una de ellas que sea dividido armónicamente por el otro. De hecho, la potencia de O con respecto a la circunferencia (c') es OA2 = OP' × OQ'. Por lo tanto, se tiene que OP2 = O2X = OP' × OQ'.
La cuaterna [P, Q, P', Q'] forma una división armónica según la relación de Newton.
Aplicación: dada una circunferencia (c) y un punto M, distinto del centro O y no perteneciente a la circunferencia, para encontrar las circunferencias ortogonales a (c) que pasan por M, basta con trazar el diámetro [PQ] sobre la recta (OM) y encontrar el punto M' tal que [P, Q, M, M'] sea una cuaterna armónica:
.
Cualquier circunferencia que pase por M y M', centrada en la bisectriz perpendicular de [MM'], es ortogonal a (c).
El conjunto de circunferencias que pasan por M y son ortogonales a (c), es un haz de circunferencias con puntos base M y M'.
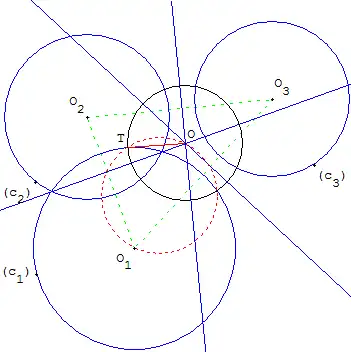
Circunferencia ortogonal a tres circunferencias (con centros no alineados)
Es la circunferencia, llamado antiguamente a veces «circunferencia ortotómica», cuyo centro O es el centro radical de las tres circunferencias y cuyo radio es igual a la raíz de la potencia p del punto O con respecto a una de las tres circunferencia. Si O está dentro de las circunferencias, p es negativo, el problema no tiene solución en el plano métrico real.
Haces ortogonales

Dadas dos circunferencias no concéntricas (c) y (c1), existen infinitas circunferencias (γ) ortogonales a (c) y (c1), que también son ortogonales a todos los círculos del haz determinado por (c) y (c1).
Las circunferencias (γ) ortogonales a las circunferencias (c) de un haz F forman un haz Φ conjugado de F. El eje radical de uno de los haces es la línea recta de los centros del otro.
Si uno de los haces está formado por circunferencias tangentes, el otro también lo está. De lo contrario, si uno de los haces tiene puntos base, el otro tiene puntos límite y existe una identidad entre estos pares de puntos.
Véase también
- Ortogonalidad (matemática)
- Eje radical
- Centro radical
- Circunferencia de Apolonio
- Coordenadas bipolares
Referencias
- ↑ Matematicas. Profesores de Enseñanza Secundaria. Volumen Ii. E-book. MAD-Eduforma. 2003. p. 317. ISBN 9788466512633. Consultado el 3 de mayo de 2025.
Bibliografía
- Chaplick, Steven; Förster, Henry; Kryven, Myroslav; Wolff, Alexander (2019). «On arrangements of orthogonal circles». En Archambault, D.; Tóth, C., eds. Graph Drawing and Network Visualization, Proceedings of the 27th International Symposium. GD 2019, Prague, Czech Republic, September 17–20, 2019. Springer. pp. 216-229. arXiv:1907.08121. doi:10.1007/978-3-030-35802-0_17.
- Court, Nathan Altshiller (1952) [1st ed. 1925], «8.B. Orthogonal Circles», College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd edición), Barnes & Noble, pp. §§ 263-272 (174-177).
- Coxeter, H. S. M.; Greitzer, S. L. (1967), Geometry Revisited, MAA, p. 115.
- Fraivert, David; Stupel, Moshe (2022), «Necessary and sufficient conditions for orthogonal circles», International Journal of Mathematical Education in Science and Technology 53 (10): 2837-2848, doi:10.1080/0020739X.2021.1945153.