Caída de Turing

Turing Tumble es un juego que introduce la función de puertas lógicas como los flip-flops y permite la programación de cálculos mecánicos simples.

Paul y Alyssa Boswell desarrollaron el juego entre 2015 y 2017. Una idea similar se desarrolló en 1965 y se llamó Digi-Comp II.

El nombre del juego deriva de Alan Turing. Se ha demostrado que, suponiendo un tablero de juego infinitamente expandible, el concepto es P-completo^[1]​ o Turing-completoy,^[2]​ por lo tanto, puede emular una máquina de Turing. Un requisito clave para una potencia similar a la de Turing es la implementación de una memoria de acceso aleatorio. Esto se puede lograr utilizando los bits de engranaje.^[3]​

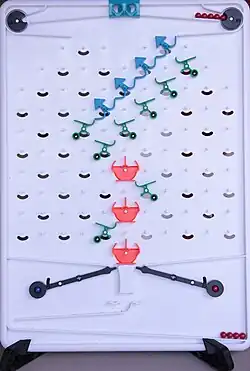
Bautizado con el nombre de Alan Turing, el juego podría, en abstracto, duplicar los procesos de cualquier computadora si el campo de juego fuera lo suficientemente grande. Esto se debe a que el juego es P-completo según el problema del valor del circuito y PSPACE-completo si se permite un número exponencial de canicas. El dispositivo tiene implicaciones para la nanotecnología.

El juego se publicita como Turing completo: una extensión del juego que permite un tablero infinitamente grande y una cantidad infinita de piezas se ha demostrado que es Turing completo mediante simulaciones tanto de la Regla 110 para autómatas celulares como de máquinas de Turing. Aunque se asemeja a una máquina de pachinko por su estética de bolas metálicas impulsadas por la gravedad, es principalmente un recurso didáctico sobre los fundamentos de la lógica y la programación informática, y como tal, un ejemplo de gamificación. El recurso que enmarca el cómic incluido presenta a un astronauta que debe resolver 60 problemas de lógica de dificultad creciente que ilustran los fundamentos de la programación informática.

En un tablero de juego casi vertical, las bolas que caen son guiadas por bloques de construcción enchufables. Cada bloque puede cambiar entre dos posiciones (bits), lo que modifica la trayectoria de la siguiente bola. Solo hay una bola en movimiento a la vez. Las bolas se liberan de uno de los dos depósitos superiores (el izquierdo para las bolas azules y el derecho para las rojas) mediante una palanca en la parte inferior del tablero. La palanca izquierda libera una bola del depósito izquierdo y la palanca derecha, del depósito derecho. Inicialmente, una de las palancas se libera manualmente. La trayectoria establecida conduce la bola que cae hacia una de las dos palancas, que libera automáticamente la siguiente bola del depósito asignado. El proceso finaliza cuando el depósito que debe proporcionar la siguiente bola está vacío o cuando la bola es guiada hacia un bloque de construcción recolector y, por lo tanto, ya no puede liberar una nueva bola. El objetivo del juego puede ser crear un patrón predeterminado de bolas azules y rojas en el canal colector al fondo del área de juego o lograr ciertas constelaciones de bloques cambiantes. Estos bloques de dos posiciones pueden interpretarse como bits y, por lo tanto, representar memoria o contadores.^[4]​

Las bolas siempre se mueven de un bloque a otro, ya sea de abajo a la izquierda o de abajo a la derecha. El juego de bloques consta de:

• Guías de pelota: dirigir la pelota en una dirección específica (objetivos de caída en verde), cruzar caminos (intersección en naranja) d. es decir, una pelota desde la izquierda se dirige a la derecha y viceversa.
• Bits (azules) con dos estados (posiciones) que, según su estado, dirigen la bola en una u otra dirección, cambiando así su estado. También hay bits conectados (bits de rueda dentada en púrpura y rojo), donde el cambio de estado de un bit provoca el cambio de estado de otros bits conectados mediante engranajes, que pueden utilizarse, por ejemplo, para... a. Se pueden realizar estados persistentes y lecturas no destructivas.
• Bloque receptor (receptor en negro) que atrapa una pelota y de esta manera detiene el proceso.^[5]​

^[6]​ ^[7]​ ^[8]​ ^[9]​ ^[10]​

Estos componentes pueden utilizarse para crear procesos complejos, como la simulación de contadores digitales, así como operaciones como la suma o la comparación. Se trata de una computadora mecánica.

Se pueden encontrar en línea varias escuelas y centros de formación de docentes que ofrecen sugerencias para su uso en el aula o en la práctica. La Escuela Normal de Baja Austria afirma:

Turing Tumble lehrt eine Reihe von Konzepten und Fähigkeiten, die für Computer, Programmierung und digitale Elektronik grundlegend sind. Die Konzepte umfassen Logikgatter, Wahrheitstabellen, Bedingungen und binäre Operationen sowie den Entwurf digitaler Schaltungen.

Gerhard Brandhofer

La Universidad Técnica de Berlín prevé su uso en los grados 5 a 10 y también ha elaborado un programa para este propósito.

En 2018, el juego fue nombrado el "Mejor Juguete STEM en general". STEM es el término en inglés para MINT. Otra reseña también clasifica el juego como STEM, especialmente en los temas de programación e informática.

• Descripción del juego en Upper Story, LLC
• Simulador de Jesse Crossen en Github
• Simulador de Rick Twilton