Cálculo vectorial

El cálculo vectorial o multivariable, también llamado análisis vectorial, es la rama de las matemáticas que aplica los conceptos del análisis matemático a las funciones vectoriales. Estas son funciones entre espacios vectoriales, es decir, que pueden tener varias variables y dan como resultado un vector en una o varias dimensiones. El cálculo vectorial estudia los límites, continuidad, diferenciabilidad e integración de estas funciones, de modo análogo a como el análisis real estudia las funciones reales de una variable.

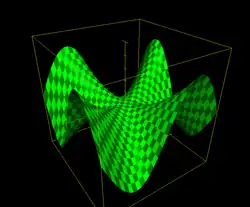
El cálculo vectorial tiene importantes aplicaciones en física e ingeniería. Muchas magnitudes en física pueden estudiarse mediante campos vectoriales, que asocian un vector a cada punto en el espacio (o un escalar en el caso particular de los campos escalares) y por tanto son funciones vectoriales. Por ejemplo, la distribución de temperaturas de la atmósfera es un campo escalar: cada punto tiene asociado un valor de temperatura distinto que varía gradualmente de un punto a otro. Por contra, la velocidad del viento es un campo vectorial: cada punto tiene asociado un vector que representa la dirección y magnitud del flujo de aire.

La derivada de una función vectorial es técnicamente una aplicación lineal y por tanto viene dada por una matriz, llamada matriz jacobiana. En el caso particular de los campos escalares la derivada es una matriz fila (un vector) llamada gradiente que apunta en la dirección hacia la que más aumenta el valor del campo. Otros operadores diferenciales de interés son el rotacional (o rotor), la divergencia y el laplaciano. La integración de funciones a lo largo de un dominio de dimensión superior a uno se resuelve, gracias al Teorema de Fubini, mediante integrales múltiples, siendo necesarias tantas como dimensiones tenga el espacio. Los teoremas de Green, de Stokes y de la divergencia relacionan varias de estas operaciones entre sí.

El cálculo vectorial se vale de las herramientas del análisis (tradicionalmente llamado cálculo infinitesimal) y del álgebra lineal. Su ámbito de estudio son los espacios euclídeos, reales o complejos, y las funciones entre estos. A su vez, la generalización a variedades (como pueden ser las superficies) es la geometría diferencial.

Historia

El estudio de los vectores se origina con la invención de los cuaterniones de Hamilton, quien junto a otros los desarrollaron como herramienta matemáticas para la exploración del espacio físico. Pero los resultados fueron desilusionantes, porque vieron que los cuaterniones eran demasiado complicados para entenderlos con rapidez y aplicarlos fácilmente.

Los cuaterniones contenían una parte escalar y una parte vectorial, y las dificultades surgían cuando estas partes se manejaban al mismo tiempo. Los científicos se dieron cuenta de que muchos problemas se podían manejar considerando la parte vectorial por separado y así comenzó el Análisis Vectorial.

Este trabajo se debe principalmente al físico estadounidense Josiah Willard Gibbs (1839-1903) y al físico matemático inglés Oliver Heaviside^[1] (1850-1925).

Recientemente, se ha desarrollado el Cálculo Fraccional de Conjuntos (en inglés, Fractional Calculus of Sets o FCS) como una metodología derivada del Cálculo Fraccional. Esta metodología, mencionada por primera vez en el artículo "Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods",^[2] tiene como objetivo caracterizar y organizar los elementos del cálculo fraccional mediante el uso de conjuntos, aprovechando la variedad de operadores fraccionales disponibles en la literatura.^[3]^[4]^[5]^[6]^[7]^[8]

Actualmente, el cálculo fraccional carece de una definición unificada de lo que constituye una derivada fraccional. En consecuencia, cuando no es necesario especificar explícitamente la forma de una derivada fraccional, típicamente se denota de la siguiente manera:

{\frac {d^{\alpha }}{dx^{\alpha }}}.

Los operadores fraccionales tienen varias representaciones, pero una de sus propiedades fundamentales es que recuperan los resultados del cálculo tradicional a medida que $\alpha \to n$ . Considerando una función escalar $h:\mathbb {R} ^{m}\to \mathbb {R}$ y la base canónica de $\mathbb {R} ^{m}$ denotada por $\{{\hat {e}}_{k}\}_{k\geq 1}$ , el siguiente operador fraccional de orden $\alpha$ se define utilizando notación de Einstein:^[9]

o_{x}^{\alpha }h(x):={\hat {e}}_{k}o_{k}^{\alpha }h(x).

Denotando $\partial _{k}^{n}$ como la derivada parcial de orden $n$ con respecto al componente $k$ -ésimo del vector $x$ , se define el siguiente conjunto de operadores fraccionales:

O_{x,\alpha }^{n}(h):=\left\{o_{x}^{\alpha }:\exists o_{k}^{\alpha }h(x){\text{ y }}\lim _{\alpha \to n}o_{k}^{\alpha }h(x)=\partial _{k}^{n}h(x)\ \forall k\geq 1\right\}.

Cálculo diferencial en campos escalares y vectoriales

Funciones de Rⁿ en R^m. Campos escalares y vectoriales

Formularemos las definiciones para campos vectoriales. También serán válidas para campos escalares. Sea

\mathbf {f} :V\longrightarrow W

un campo vectorial que hace corresponder a todo punto P definido biunívocamente por su vector posición, un vector $\mathbf {f} {\big (}\mathbf {OP} {\big )}$ donde el punto O es nuestro origen de coordenadas.

V\subseteq \mathbb {R} ^{n},W\subseteq \mathbb {R} ^{m},

con

n>1

y

m\geqslant 1

. Cuando

m=1

tenemos un campo escalar. Para

m>1

tenemos un campo vectorial. Utilizaremos la norma euclídea para hallar la magnitud de los vectores.

Límites y continuidad

Si $\mathbf {a} \in \mathbb {R} ^{n}$ y $\mathbf {b} \in \mathbb {R} ^{m}.$ Escribimos:

\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b}

,

o bien,

\mathbf {f} (\mathbf {x} )\rightarrow \mathbf {b}

cuando

\mathbf {x} \rightarrow \mathbf {a}

para expresar lo siguiente:

\lim _{{\big \|}\mathbf {x-a} {\big \|}\to 0}{\big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\big \|}=0

donde ${\big \|}\mathbf {x} {\big \|}$ es la norma euclídea de $\mathbf {x}$ . Expresándolo en función de las componentes de $\mathbf {x} ={\big (}x_{1},\ldots ,x_{n}{\big )},\mathbf {a} ={\big (}a_{1},\ldots ,a_{n}{\big )},$

\lim _{{\big (}x_{1},\ldots ,x_{n}{\big )}\to {\big (}a_{1},\ldots ,a_{n}{\big )}}\mathbf {f} {\big (}x_{1},\ldots ,x_{n}{\big )}=\mathbf {b}

o, de forma equivalente,

\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b}

Decimos que una función $\mathbf {f}$ es continua en $\mathbf {a} \Leftrightarrow \lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {f} {\big (}\mathbf {a} {\big )}$

$\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\big (}\mathbf {x} {\big )}=\mathbf {b} ,\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {g} {\big (}\mathbf {x} {\big )}=\mathbf {c} \Rightarrow$

a) $\lim _{\mathbf {x} \to \mathbf {a} }{\big [}\mathbf {f} +\mathbf {g} {\big ]}{\big (}\mathbf {x} {\big )}=\mathbf {b} +\mathbf {c}$

b) $\lim _{\mathbf {x} \to \mathbf {a} }\lambda \mathbf {f} {\big (}\mathbf {x} {\big )}=\lambda \mathbf {b} \quad \forall \lambda \in \mathbb {R}$

c) $\lim _{\mathbf {x} \to \mathbf {a} }{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\mathbf {b} \cdot \mathbf {c}$

(producto escalar de $\mathbf {b}$ con $\mathbf {c}$ ).

d) $\lim _{\mathbf {x} \to \mathbf {a} }{\Big \|}\mathbf {f} {\big (}\mathbf {x} {\big )}{\Big \|}={\big \|}\mathbf {b} {\big \|}$

Demostración
Sabemos que a) y b) en el teorema se verifican si $f$ y $g$ son funciones escalares. Por tanto, si $\mathbf {b} ={\big (}b_{1},\ldots ,b_{m}{\big )},\mathbf {c} ={\big (}c_{1},\ldots ,c_{m}{\big )}$ tenemos ${\begin{array}{rl}a)&\mathbf {f} {\big (}\mathbf {x} )={\big [}f_{1}{\big (}\mathbf {x} {\big )},\ldots ,f_{m}{\big (}\mathbf {x} {\big )}{\big ]},\mathbf {g} {\big (}\mathbf {x} )={\Big [}g_{1}{\big (}\mathbf {x} {\big )},\ldots ,g_{m}{\big (}\mathbf {x} {\big )}{\Big ]}\\&\lim _{\mathbf {x} \to \mathbf {a} }{\big (}\mathbf {f} +\mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\lim _{\mathbf {x} \to \mathbf {a} }{\Big [}{\big (}f_{1}+g_{1}{\big )}{\big (}\mathbf {x} {\big )},\ldots ,{\big (}f_{m}+g_{m}{\big )}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }{\big (}f_{1}+g_{1}{\big )}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }{\big (}f_{m}+g_{m}{\big )}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )}+\lim _{\mathbf {x} \to \mathbf {a} }g_{1}(\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}+\lim _{\mathbf {x} \to \mathbf {a} }g_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\big (}b_{1}+c_{1},\ldots ,b_{m}+c_{m}{\big )}={\big (}b_{1},\ldots ,b_{m}{\big )}+{\big (}c_{1},\ldots ,c_{m}{\big )}=\mathbf {b} +\mathbf {c} \end{array}}$ ${\begin{array}{rl}b)&\lim _{\mathbf {x} \to \mathbf {a} }\lambda \mathbf {f} {\big (}\mathbf {x} {\big )}=\lim _{\mathbf {x} \to \mathbf {a} }\lambda {\Big [}f_{1}{\big (}\mathbf {x} {\big )},\ldots ,f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\lim _{\mathbf {x} \to \mathbf {a} }{\Big [}\lambda f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lambda f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&{\Big [}\lim _{\mathbf {x} \to \mathbf {a} }\lambda f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }\lambda f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}={\Big [}\lambda \lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lambda \lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\\&\lambda {\Big [}\lim _{\mathbf {x} \to \mathbf {a} }f_{1}{\big (}\mathbf {x} {\big )},\ldots ,\lim _{\mathbf {x} \to \mathbf {a} }f_{m}{\big (}\mathbf {x} {\big )}{\Big ]}=\lambda {\big (}b_{1},\ldots ,b_{m}{\big )}=\lambda \mathbf {b} \end{array}}$ $c)\quad {\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} ={\Big [}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big ]}\cdot {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big ]}+\mathbf {b} \cdot {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big ]}+\mathbf {c} \cdot {\Big [}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big ]}$ Aplicando la desigualdad triangular y la desigualdad de Cauchy-Schwarz tenemos ${\begin{array}{l}{\Big \|}{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} {\Big \|}\leqslant {\Big \\|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \\|}\cdot {\Big \\|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \\|}+{\big \\|}\mathbf {b} {\big \\|}\cdot {\Big \\|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \\|}+{\big \\|}\mathbf {c} {\big \\|}\cdot {\Big \\|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \\|}\Rightarrow \\0\leqslant \lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \|}{\big (}\mathbf {f} \cdot \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}-\mathbf {b} \cdot \mathbf {c} {\Big \|}\leqslant \lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \\|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \\|}\cdot \lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \\|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \\|}+\\{\big \\|}\mathbf {b} {\big \\|}\cdot \lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \\|}\mathbf {g} {\big (}\mathbf {x} {\big )}-\mathbf {c} {\Big \\|}+{\big \\|}\mathbf {c} {\big \\|}\lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \\|}\mathbf {f} {\big (}\mathbf {x} {\big )}-\mathbf {b} {\Big \\|}=0\cdot 0+{\big \\|}\mathbf {b} {\big \\|}\cdot 0+{\big \\|}\mathbf {c} {\big \\|}\cdot 0=\\0\end{array}}$ , como queríamos demostrar. $d)\quad \mathbf {g} {\big (}\mathbf {x} {\big )}=\mathbf {f} {\big (}\mathbf {x} {\big )},\mathbf {c} =\mathbf {b} \Rightarrow \lim _{\mathbf {x} \to \mathbf {a} }{\Big \\|}\mathbf {f} {\big (}\mathbf {x} {\big )}{\Big \\|}^{2}={\big \\|}\mathbf {b} {\big \\|}^{2}$ , como queríamos demostrar.

Sean $\mathbf {f}$ y $\mathbf {g}$ dos funciones tales que la función compuesta $\mathbf {f} \circ \mathbf {g}$ está definida en $\mathbf {a}$ , siendo

${\big (}\mathbf {f} \circ \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}=\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}$

$\mathbf {g}$ es continua en $\mathbf {a}$ y $\mathbf {f}$ es continua en $\mathbf {g} {\big (}\mathbf {a} {\big )}\Rightarrow {\big (}\mathbf {f} \circ \mathbf {g} {\big )}$ es continua en $\mathbf {a}$ .

Demostración
Sean $\mathbf {y} =\mathbf {g} {\big (}\mathbf {x} {\big )}$ y $\mathbf {b} =\mathbf {g} {\big (}\mathbf {a} {\big )}$ . Entonces, ${\begin{array}{l}\lim _{{\big \\|}\mathbf {x} -\mathbf {a} {\big \\|}\to 0}{\Big \\|}\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}-\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {a} {\big )}{\Big ]}{\Big \\|}=\lim _{{\big \\|}\mathbf {y} -\mathbf {b} {\big \\|}\to 0}{\Big \\|}\mathbf {f} {\big (}\mathbf {y} {\big )}-\mathbf {f} {\big (}\mathbf {b} {\big )}{\Big \\|}=0\Rightarrow \\\lim _{\mathbf {x} \to \mathbf {a} }\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}=\mathbf {f} {\Big [}\mathbf {g} {\big (}\mathbf {a} {\big )}{\Big ]}\end{array}}$ como queríamos demostrar.

Derivadas direccionales

Derivada de un campo escalar respecto a un vector

Sea $f:S\subseteq \mathbb {R} ^{n}\longrightarrow \mathbb {R}$ . Sea $\mathbf {x}$ un vector cuyo origen es el origen de coordenadas y cuyo extremo $\in S,$ e $\mathbf {y}$ un vector arbitrario de $\mathbb {R} ^{n}$ . Definimos la derivada de f en $\mathbf {x}$ respecto a $\mathbf {y}$ como

$f'{\big (}\mathbf {x} ;\mathbf {y} {\big )}=\lim _{h\to 0}{\cfrac {f{\big (}\mathbf {x} +h\mathbf {y} {\big )}-f{\big (}\mathbf {x} {\big )}}{h}}$

Derivadas parciales

${\cfrac {\partial f}{\partial x_{k}}}=\lim _{h\to 0}{\cfrac {f{\big (}x_{1},\ldots ,x_{k}+h,\ldots ,x_{n}{\big )}-f{\big (}x_{1},\ldots ,x_{k},\ldots ,x_{n}{\big )}}{h}}$

Si derivamos la expresión anterior respecto a una segunda variable,

x_{j}

, tendremos

{\cfrac {\partial ^{2}f}{\partial x_{j}\partial x_{k}}}

. En la práctica, calcularemos

{\cfrac {\partial f}{\partial x_{k}}}

derivando respecto a

x_{k}

y suponiendo ctm

x_{j},\quad \forall j\neq k

constante.

La diferencial

Definición de campo escalar diferenciable

Decimos que f es diferenciable en $\mathbf {a} \Leftrightarrow$

$\exists f_{L}:\mathbb {R} ^{n}\longrightarrow \mathbb {R} {\Big |}\lim _{{\big \|}\mathbf {v} {\big \|}\to \mathbf {0} }f{\big (}\mathbf {a} +\mathbf {v} {\big )}=f{\big (}\mathbf {a} {\big )}+f_{L}{\big (}\mathbf {v} {\big )}$ .

$f_{L}$ ha de ser una aplicación lineal, que definimos como la diferencial de f en a.

La anterior ecuación es la fórmula de Taylor de primer orden para

f{\big (}\mathbf {a} +\mathbf {v} {\big )}

.

Teorema de unicidad de la diferencial

$f$ es diferenciable en $\mathbf {x}$ con diferencial $f_{L}{\big (}\mathbf {y} {\big )}\Rightarrow$

a) $\exists f'{\big (}\mathbf {x} ;\mathbf {y} {\big )}\quad \forall \mathbf {y} \in \mathbb {R} ^{n}$

b) $f'{\big (}\mathbf {x} ;\mathbf {y} {\big )}=\sum _{k=1}^{n}y_{k}{\cfrac {\partial f}{\partial x_{k}}}$

Demostración
${\begin{array}{rl}a)&\mathbf {v} =h\mathbf {y} ,\quad h\in \mathbb {R} ,\\&\lim _{{\big \\|}\mathbf {v} {\big \\|}\to \mathbf {0} }f{\big (}\mathbf {x} +\mathbf {v} {\big )}=\lim _{{\big \\|}\mathbf {v} {\big \\|}\to \mathbf {0} }f{\big (}\mathbf {x} +h\mathbf {y} {\big )}=f{\big (}\mathbf {x} {\big )}+f_{L}{\big (}h\mathbf {y} {\big )}=\\&f{\big (}\mathbf {x} {\big )}+hf_{L}{\big (}\mathbf {y} {\big )}\Rightarrow \\&\lim _{h\to 0}{\cfrac {f{\big (}\mathbf {x} +h\mathbf {y} {\big )}-f{\big (}\mathbf {x} {\big )}}{h}}=f'{\big (}\mathbf {x} ;\mathbf {y} {\big )}=f_{L}{\big (}\mathbf {y} {\big )}\end{array}}$ como queríamos demostrar. $b)$ Expresando $y$ en función de sus componentes en la base ${\begin{array}{l}{\big \{}\mathbf {e} _{1},\ldots ,\mathbf {e} _{n}{\big \}},f_{L}{\big (}\mathbf {y} {\big )}=f_{L}{\big (}\sum _{k=1}^{n}y_{k}\mathbf {e} _{k}{\big )}=\sum _{k=1}^{n}y_{k}f_{L}{\big (}\mathbf {e} _{k}{\big )}=\sum _{k=1}^{n}y_{k}f'{\big (}\mathbf {x} ;\mathbf {e} _{k}{\big )}=\\\sum _{k=1}^{n}y_{k}{\cfrac {\partial f}{\partial x_{k}}}\end{array}}$ como queríamos demostrar.

Regla de la cadena

Sea $f:S\subset \mathbb {R} ^{n}\longrightarrow \mathbb {R}$ un campo escalar y $\mathbf {x} :J\subset \mathbb {R} \longrightarrow S$ . Definimos la función compuesta $g=f\circ \mathbf {x}$ como $g(t)=f{\Big [}\mathbf {x} {\big (}t{\big )}{\Big ]}$ , entonces $\quad g'{\big (}t{\big )}=\sum _{k=1}^{n}{\cfrac {\partial f}{\partial x_{k}}}\cdot {\cfrac {dx_{k}}{dt}}$

Diferencial de un campo vectorial

Sea $\mathbf {f} :S\subseteq \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}$ un campo vectorial. Sea $\mathbf {x} \in S$ e $\mathbf {y}$ un vector cualquiera. Definimos la derivada

$\mathbf {f'} {\big (}\mathbf {x} ;\mathbf {y} {\big )}=\lim _{h\to 0}{\cfrac {\mathbf {f} {\big (}\mathbf {x} +h\mathbf {y} {\big )}-\mathbf {f} {\big (}\mathbf {x} {\big )}}{h}}$

Expresando $\mathbf {f'} {\big (}\mathbf {x} ;\mathbf {y} {\big )}$ en función de sus componentes, tenemos $\mathbf {f'} {\big (}\mathbf {x} ;\mathbf {y} {\big )}={\Big [}f'_{1}{\big (}\mathbf {x} ;\mathbf {y} {\big )},\ldots ,f'_{m}{\big (}\mathbf {x} ;\mathbf {y} {\big )}{\Big ]}$

Decimos que $\mathbf {f}$ es diferenciable $\Leftrightarrow \exists \mathbf {f} _{L}:\mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}$ , aplicación lineal que verifica:

$\lim _{{\big \|}\mathbf {v} {\big \|}\to 0}\mathbf {f} {\big (}\mathbf {x} +\mathbf {v} {\big )}=\mathbf {f} {\big (}\mathbf {x} {\big )}+\mathbf {f} _{L}{\big (}\mathbf {v} {\big )}$ .

Esta es la fórmula de Taylor de primer orden para

\mathbf {f} .\quad \mathbf {f} _{L}{\big (}\mathbf {v} {\big )}=\mathbf {f} '{\big (}\mathbf {x} ;\mathbf {v} {\big )}

.

La matriz de $\mathbf {f} '$ es su matriz jacobiana.

Diferenciabilidad implica continuidad

Si un campo vectorial $\mathbf {f}$ es diferenciable en $\mathbf {x} \Rightarrow$ es continuo en $\mathbf {x}$ .

Se deduce fácilmente de la fórmula de Taylor de primer orden ya vista.

Regla de la cadena para diferenciales de campos vectoriales

Sea $\mathbf {h} {\big (}\mathbf {x} {\big )}={\big (}\mathbf {f} \circ \mathbf {g} {\big )}{\big (}\mathbf {x} {\big )}$ un campo vectorial definido y diferenciable en $\mathbf {x}$ . Su diferencial $\mathbf {h} '{\big (}\mathbf {x} {\big )}$ resulta ser

$\mathbf {h} '{\big (}\mathbf {x} {\big )}=\mathbf {f} '{\Big [}\mathbf {g} {\big (}\mathbf {x} {\big )}{\Big ]}\circ \mathbf {g} '{\big (}\mathbf {x} {\big )}$

Condición suficiente para la igualdad de las derivadas parciales mixtas

${\cfrac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}={\cfrac {\partial ^{2}f}{\partial x_{j}\partial x_{i}}}\quad \forall i\neq j\Leftrightarrow$ ambas derivadas parciales existen y son continuas en $\mathbf {x}$ .

Aplicaciones del cálculo diferencial

Cálculo de máximos, mínimos y puntos de ensilladura para campos escalares

Un campo escalar tiene un máximo en $\mathbf {x} =\mathbf {a} \Leftrightarrow$ existe una n-bola $B{\big (}\mathbf {a} {\big )}{\Big |}\forall \mathbf {x} \in B{\big (}\mathbf {a} {\big )}\quad f{\big (}\mathbf {x} {\big )}\leqslant f{\big (}\mathbf {a} {\big )}$

Un campo escalar tiene un mínimo en $\mathbf {x} =\mathbf {a} \Leftrightarrow$ existe una n-bola $B{\big (}\mathbf {a} {\big )}{\Big |}\forall \mathbf {x} \in B{\big (}\mathbf {a} {\big )}\quad f{\big (}\mathbf {x} {\big )}\geqslant f{\big (}\mathbf {a} {\big )}$

Un campo escalar tiene un punto de ensilladura $\Leftrightarrow$

$\forall B{\big (}\mathbf {a} {\big )}\quad \exists \mathbf {x} {\big |}f{\big (}\mathbf {x} {\big )}\leqslant f{\big (}\mathbf {a} {\big )}\land \exists \mathbf {x} {\big |}f{\big (}\mathbf {x} {\big )}\geqslant f{\big (}\mathbf {a} {\big )}$ .

Para saber si es uno de los casos anteriores:

Obtenemos $\mathbf {x} {\Big |}{\cfrac {\partial f}{\partial x_{k}}}=0\qquad \forall k{\Big |}1\leqslant k\leqslant n$
Obtenemos la matriz hessiana de f. Sea esta $\mathbf {F} {\big (}\mathbf {x} {\big )}$ $\mathbf {F} {\big (}\mathbf {x} {\big )}$ .
1. $\mathbf {F} {\big (}\mathbf {x} {\big )}$ es definida positiva $\Rightarrow f$ tiene un mínimo local (mínimo relativo) en $\mathbf {x}$ .
2. $\mathbf {F} {\big (}\mathbf {x} {\big )}$ es definida negativa $\Rightarrow f$ tiene un máximo local (máximo relativo) en $\mathbf {x}$ .
3. $\mathbf {F} {\big (}\mathbf {x} {\big )}$ es indefinida $\Rightarrow f$ tiene un punto de ensilladura en $\mathbf {x}$ .

En lo anteriormente expuesto, hemos supuesto que ${\cfrac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}$ es continua $\forall i,j{\big |}1\leqslant i\leqslant n,1\leqslant j\leqslant n$

Véase también

Referencias

Bibliografía

Apostol, Tom M., Calculus, volumen 2, editorial reverté, S. A., ISBN 84-291-5003-X
Luis Santaló (1977) Vectores y Tensores con sus Aplicaciones, Editorial Universitaria de Buenos Aires.

Enlaces externos

Wikiversidad alberga proyectos de aprendizaje sobre Cálculo vectorial.
Portal:Matemática. Contenido relacionado con Matemática.
Portal:Física. Contenido relacionado con Física.

Datos: Q200802
Multimedia: Vector calculus / Q200802

[1] ttp://worrydream.com/refs/Crowe-HistoryOfVectorAnalysis.pdf sección 5

[2] Sets of Fractional Operators and Numerical Estimation of the Order of Convergence of a Family of Fractional Fixed-Point Methods

[3] A review of definitions for fractional derivatives and integral

[4] A review of definitions of fractional derivatives and other operators

[5] How many fractional derivatives are there?

[6] Acceleration of the order of convergence of a family of fractional fixed-point methods and its implementation in the solution of a nonlinear algebraic system related to hybrid solar receivers

[7] Code of a multidimensional fractional quasi-Newton method with an order of convergence at least quadratic using recursive programming

[8] Sets of Fractional Operators and Some of Their Applications

[9] Einstein summation for multidimensional arrays

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]