Beta termodinámica

En la termodinámica estadística, la beta termodinámica, también conocida como frialdad,^[1]​ es el recíproco de la temperatura termodinámica de un sistema:$${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$$ (donde T es la temperatura y k_B es la constante de Boltzmann).^[2]​

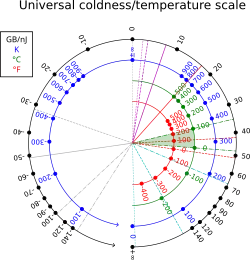
La beta termodinámica tiene unidades recíprocas a las de la energía (en unidades SI, recíprocos de julios, ${\displaystyle [\beta ]={\textrm {J}}^{-1}}$). En unidades no térmicas, también puede medirse en byte por julio, o más convenientemente, gigabyte por nanojulio;^[3]​ 1 K⁻¹ equivale a aproximadamente 13,062 gigabytes por nanojulio; a temperatura ambiente: T = 300K, β ≈ 44 GB/nJ ≈ 39 eV⁻¹ ≈ 2.4×10²⁰ J⁻¹. El factor de conversión es 1 GB/nJ = ${\displaystyle 8\ln 2\times 10^{18}}$ J⁻¹.

La beta termodinámica es esencialmente la conexión entre la teoría de la información y la interpretación de la mecánica estadística de un sistema físico a través de su entropía y la termodinámica asociada con su energía. Expresa la respuesta de la entropía ante un aumento de energía. Si se añade una pequeña cantidad de energía al sistema, entonces β describe cuánto se aleatorizará el sistema.

Mediante la definición estadística de la temperatura como función de la entropía, la función de frialdad puede calcularse en el conjunto microcanónico a partir de la fórmula

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}},={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(es decir, la derivada parcial de la entropía S respecto a la energía E a volumen constante V y número de partículas N).

Aunque es completamente equivalente en contenido conceptual a la temperatura, β se considera generalmente una cantidad más fundamental que la temperatura debido al fenómeno de la temperatura negativa, en el cual β es continua al cruzar cero mientras que T presenta una singularidad.^[4]​

Además, β tiene la ventaja de ser más fácil de entender causalmente: si se añade una pequeña cantidad de calor a un sistema, β es el aumento de entropía dividido por el aumento de calor. La temperatura es difícil de interpretar en el mismo sentido, ya que no es posible "añadir entropía" a un sistema excepto indirectamente, modificando otras cantidades como la temperatura, el volumen o el número de partículas.

Desde el punto de vista estadístico, β es una cantidad numérica que relaciona dos sistemas macroscópicos en equilibrio. La formulación exacta es la siguiente. Consideremos dos sistemas, 1 y 2, en contacto térmico, con energías respectivas E₁ y E₂. Suponemos que E₁ + E₂ = una constante E. El número de microestados de cada sistema se denotará por Ω₁ y Ω₂. Bajo nuestras suposiciones, Ω_i depende solo de E_i. También asumimos que cualquier microestado del sistema 1 consistente con E₁ puede coexistir con cualquier microestado del sistema 2 consistente con E₂. Por lo tanto, el número de microestados para el sistema combinado es

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}(E-E_{1}).,}$

Derivaremos β a partir de la suposición fundamental de la mecánica estadística:

Cuando el sistema combinado alcanza el equilibrio, el número Ω se maximiza.

(En otras palabras, el sistema busca naturalmente el número máximo de microestados.) Por lo tanto, en equilibrio,

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Pero E₁ + E₂ = E implica

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Así que

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

es decir,

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{en equilibrio.}}}$

La relación anterior motiva una definición de β:

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Cuando dos sistemas están en equilibrio, tienen la misma temperatura termodinámica T. Por lo tanto, intuitivamente, se esperaría que β (definida a través de microestados) esté relacionada de alguna manera con T. Este vínculo lo proporciona la suposición fundamental de Boltzmann escrita como

${\displaystyle S=k_{\rm {B}}\ln \Omega ,}$

donde k_B es la constante de Boltzmann, S es la entropía termodinámica clásica y Ω es el número de microestados. Así,

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Sustituyendo en la definición de β desde la definición estadística anterior da

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Comparando con la fórmula termodinámica

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

tenemos

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

donde ${\displaystyle \tau }$ se llama la temperatura fundamental del sistema y tiene unidades de energía.

La beta termodinámica fue introducida originalmente en 1971 (como Kältefunktion "función de frialdad") por Ingo Müller, uno de los defensores de la escuela de pensamiento de la termodinámica racional^[5]​^[6]​ basándose en propuestas anteriores para una función de "temperatura recíproca".^[1]​^[7]​

Distribución de Boltzmann

Conjunto canónico

Modelo de Ising