Anexo:Galería de grafos
A continuación se lista una galería de grafos que se distinguen por su tipología o propiedades.
Familias de grafos
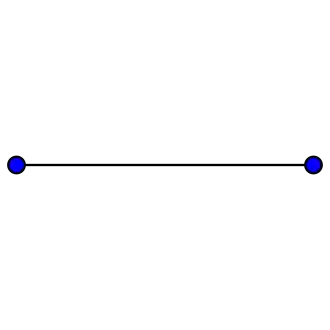
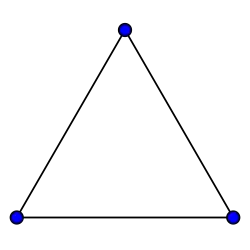
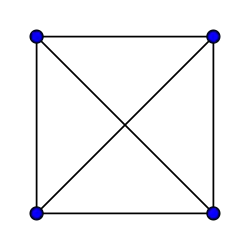
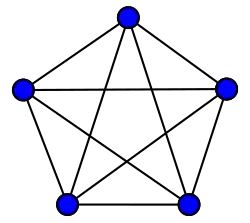
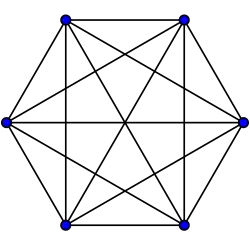
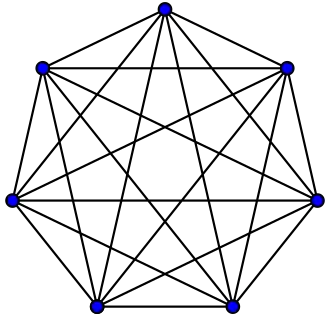
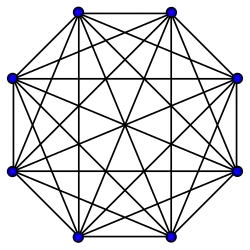
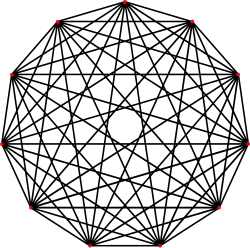
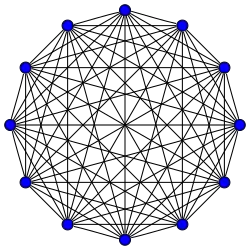
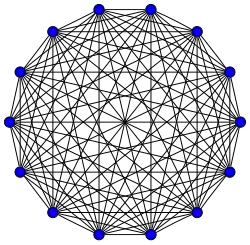
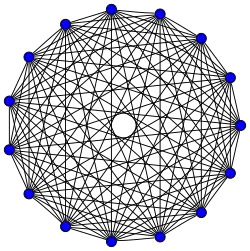
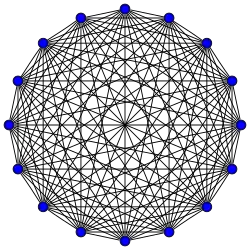
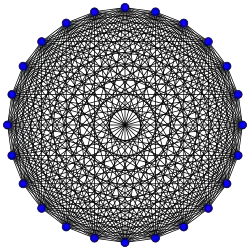
Grafos completos
El grafo completo de vértices es a menudo llamado El -clique y por lo general denotado como , del alemán komplett.[1]
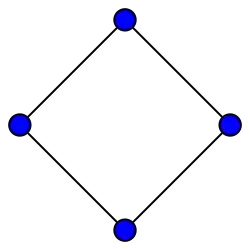
Grafos completos bipartitos
El Grafo bipartito completo es por lo general denotado . Para grafos de fórmula ver mejor la sección 1.9 grafos estrella. El grafo bipartito completo es igual que el grafo ciclo (el cuadrado) mostrado en la sección grafos ciclo.
-

-
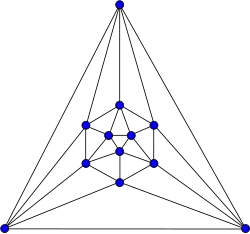
 , grafo de Thomsen
, grafo de Thomsen -

-

-

-

-

-

-

-

-

-

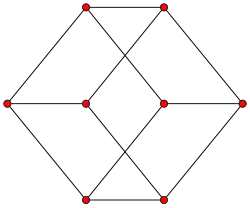
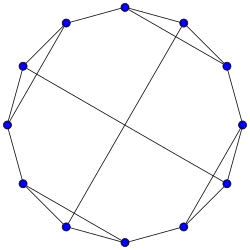
Ciclos
Los grafos cíclicos de vértices son denominados n-ciclos y generalmente son denotados como . También son llamados polígonoso n-gonos. Casos especiales son el triángulo , el cuadrado , y todos los restantes polígonos convexos, como pentágono , hexágono , etc.
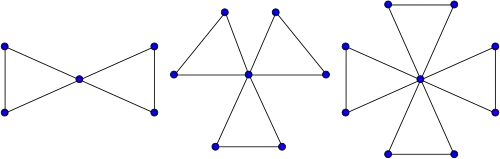
Grafos de la amistad
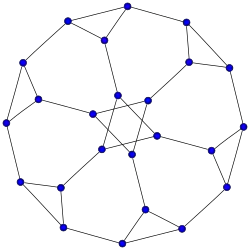
Grafos de fullerenos
-
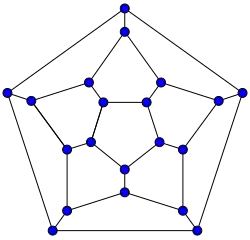 20-fullereno (grafo dodecaédrico)
20-fullereno (grafo dodecaédrico) -
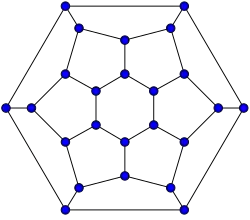 24-fullereno (grafo trapezoedro hexagonal truncado)
24-fullereno (grafo trapezoedro hexagonal truncado) -
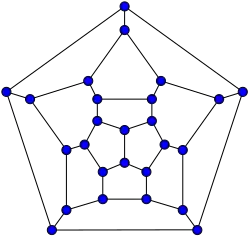 26-fullereno
26-fullereno -
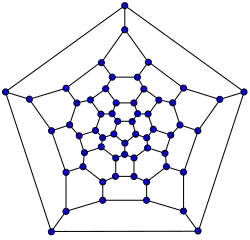 60-fullereno (grafo icosaédrico truncado)
60-fullereno (grafo icosaédrico truncado) -
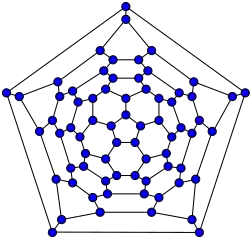 70-fullereno
70-fullereno
Sólidos platónicos
Sólidos platónicos truncados
Snarks
-
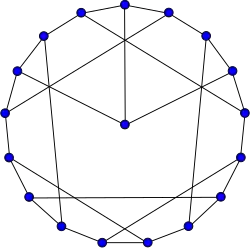 Snark de Blanuša (primero)
Snark de Blanuša (primero) -
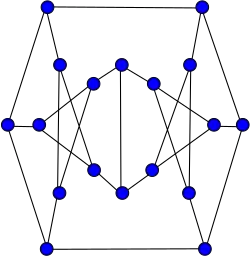 Snark de Blanuša (segundo)
Snark de Blanuša (segundo) -
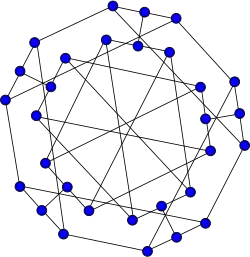 Snark doble estrellado
Snark doble estrellado -
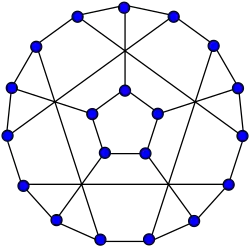 Snark flor
Snark flor -
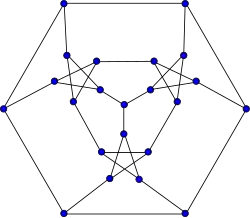 Snark de Loupekine (primero)
Snark de Loupekine (primero) -
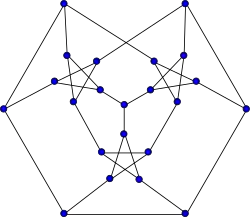 Snark de Loupekine (segundo)
Snark de Loupekine (segundo) -
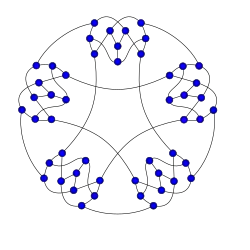 Snark de Szekeres
Snark de Szekeres -
 Grafo de Tietze
Grafo de Tietze -
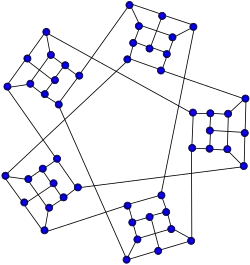 Snark de Watkins
Snark de Watkins
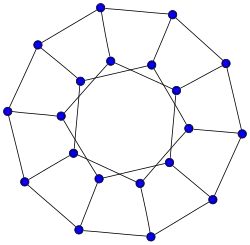
Estrellas

Ruedas

Grafos individuales
-

-
 11-jaula de Balaban
11-jaula de Balaban -

-
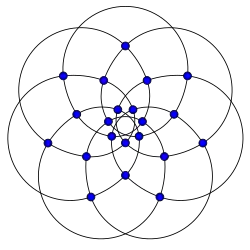 Grafo de Brinkmann
Grafo de Brinkmann -

-

-
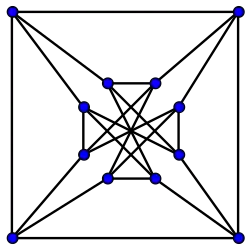
-
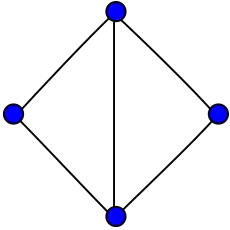
-

-
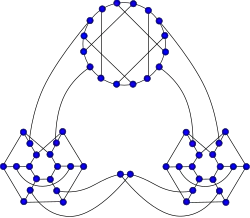 Grafo 54 de Ellingham–Horton
Grafo 54 de Ellingham–Horton -
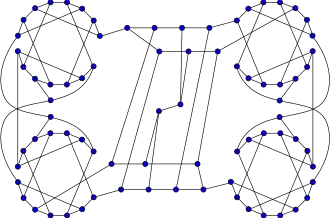 Grafo 78 de Ellingham–Horton
Grafo 78 de Ellingham–Horton -
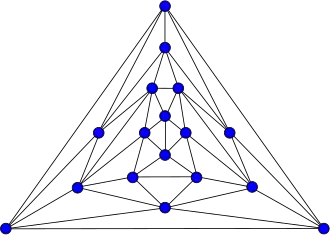 Grafo de Errera
Grafo de Errera -
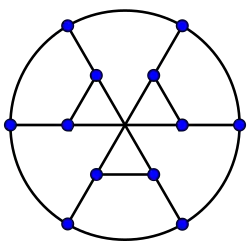 Grafo de Franklin
Grafo de Franklin -
 Grafo de Frucht
Grafo de Frucht -
 Grafo de Goldner-Harary
Grafo de Goldner-Harary -
 Grafo de Grötzsch
Grafo de Grötzsch -
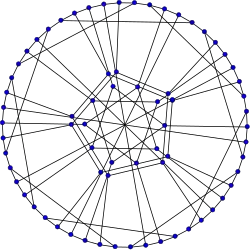 Grafo de Harries
Grafo de Harries -
 Grafo de Harries-Wong
Grafo de Harries-Wong -
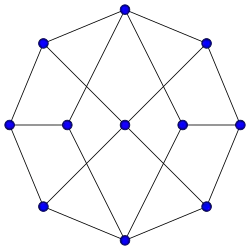
-
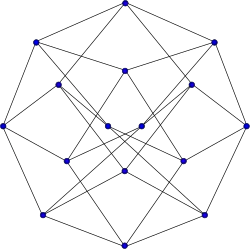 Grafo de Hoffman
Grafo de Hoffman -
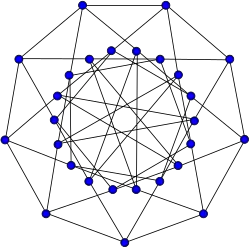 Grafo de Holt
Grafo de Holt -
 Grafo de Horton
Grafo de Horton -
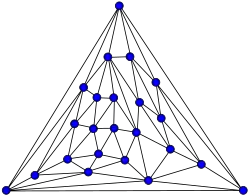 Grafo de Kittell
Grafo de Kittell -
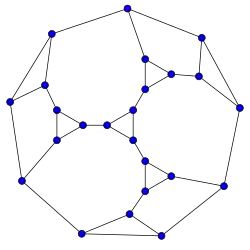 Grafo de Markström
Grafo de Markström -
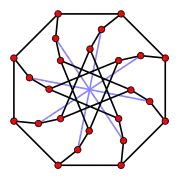
-
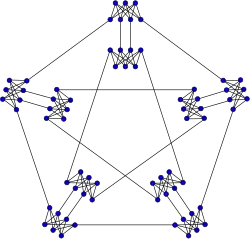 Grafo de Meredith
Grafo de Meredith -
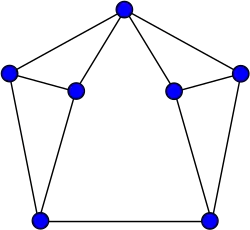 Huso de Moser
Huso de Moser -
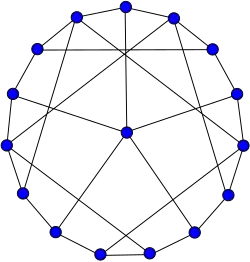 Grafo de Sousselier
Grafo de Sousselier -
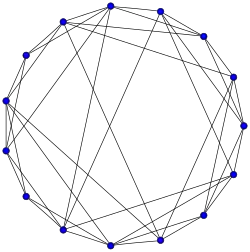 Grafo de Poussin
Grafo de Poussin -
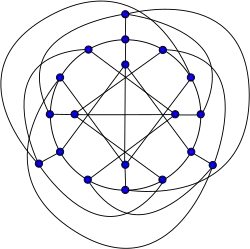 Grafo de Robertson
Grafo de Robertson -
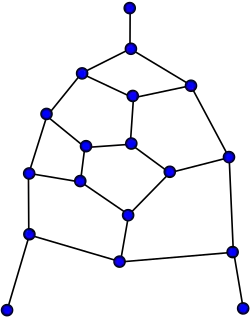 Fragmento de Tutte
Fragmento de Tutte -
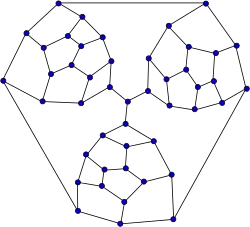 Grafo de Tutte
Grafo de Tutte -
 Grafo de Young–Fibonacci
Grafo de Young–Fibonacci -
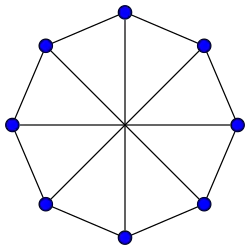 Grafo de Wagner
Grafo de Wagner -
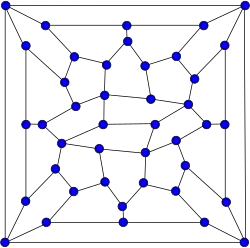 Grafo de Wiener–Araya
Grafo de Wiener–Araya
Grafos con grados de simetría
Grafos fuertemente regulares
-
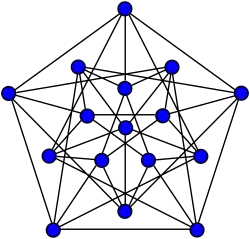
-

-
 Grafo de Hall-Janko
Grafo de Hall-Janko -
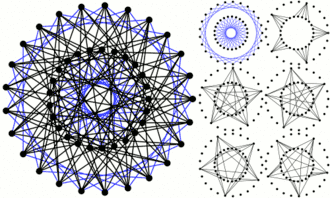 Grafo de Hoffman-Singleton
Grafo de Hoffman-Singleton -
 Grafo de Higman-Sims
Grafo de Higman-Sims -
 Grafo de Paley de orden 13
Grafo de Paley de orden 13 -
 Grafo de Shrikhande
Grafo de Shrikhande -
 Grafo de Schläfli
Grafo de Schläfli -
 Grafo de Brouwer–Haemers
Grafo de Brouwer–Haemers -
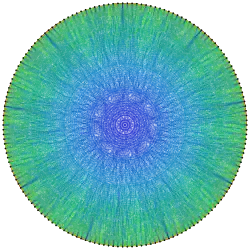 Grafo de McLaughlin local
Grafo de McLaughlin local -
 Grafo de Perkel
Grafo de Perkel -
 Grafo de Gewirtz
Grafo de Gewirtz
Grafos simétricos
-
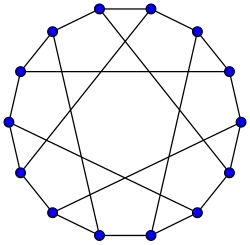
-
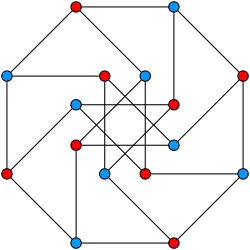
-
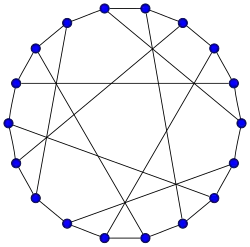
-

-
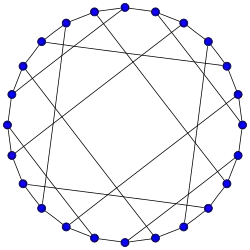
-

-

-
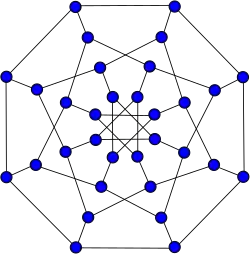
-
 Grafo de Foster
Grafo de Foster -
 Grafo de Biggs-Smith
Grafo de Biggs-Smith -
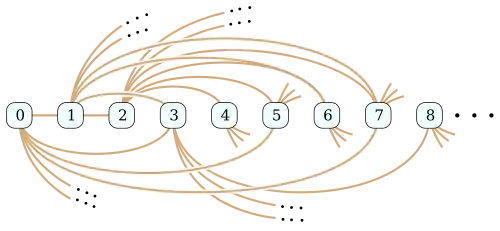 Grafo de Rado
Grafo de Rado
Grafos semi-simétricos
-
 Grafo de Folkman
Grafo de Folkman -
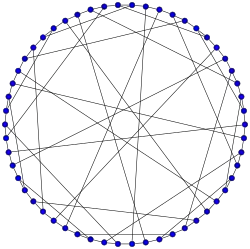 Grafo de Gray
Grafo de Gray -
 Grafo de Ljubljana
Grafo de Ljubljana -
 12-jaula de Tutte
12-jaula de Tutte
Véase también
Referencias
- ↑ David Gries and Fred B. Schneider, A Logical Approach to Discrete Math, Springer, 1993, p 436.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Galería de grafos.
Wikimedia Commons alberga una categoría multimedia sobre Galería de grafos.