Analogía de movilidad

La analogía de la movilidad, también llamada analogía de la admitancia o analogía de Firestone, es un método para representar un sistema mecánico mediante un sistema eléctrico análogo. La ventaja de hacer esto es que existe un gran cuerpo de teoría y técnicas de análisis sobre sistemas eléctricos complejos, especialmente en el campo de los filtros.^[1]​ Al convertir a una representación eléctrica, estas herramientas del dominio eléctrico pueden aplicarse directamente a un sistema mecánico sin modificaciones. Otra ventaja se da en los sistemas electromecánicos: La conversión de la parte mecánica de un sistema de este tipo al dominio eléctrico permite analizar todo el sistema como un todo unificado.

El comportamiento matemático del sistema eléctrico simulado es idéntico al comportamiento matemático del sistema mecánico representado. A cada elemento del dominio eléctrico le corresponde un elemento del dominio mecánico con una ecuación constitutiva análoga. Todas las leyes del análisis de circuitos, como las leyes de Kirchhoff, que se aplican en el dominio eléctrico también se aplican a la analogía de movilidad mecánica.

La analogía de la movilidad es una de las dos principales analogías mecánico-eléctricas utilizadas para representar sistemas mecánicos en el dominio eléctrico; la otra es la analogía de la impedancia. Los papeles de la tensión y la corriente se invierten en estos dos métodos, y las representaciones eléctricas producidas son los circuitos duales de cada uno. La analogía de la movilidad conserva la topología del sistema mecánico cuando se transfiere al dominio eléctrico, mientras que la analogía de la impedancia no. Por otra parte, la analogía de la impedancia conserva la analogía entre la impedancia eléctrica y la impedancia mecánica, mientras que la analogía de la movilidad no.

La analogía de la movilidad se utiliza ampliamente para modelar el comportamiento de los filtros mecánicos. Se trata de filtros destinados a ser utilizados en un circuito electrónico, pero que funcionan enteramente por ondas vibratorias mecánicas. En la entrada y la salida del filtro se colocan transductores para convertir entre los dominios eléctrico y mecánico.^[2]​

Otro uso muy común es en el campo de los equipos de audio, como los altavoces. Los altavoces constan de un transductor y piezas mecánicas móviles. Las ondas acústicas en sí son ondas de movimiento mecánico: de moléculas de aire o de algún otro medio fluido.^[3]​

Antes de desarrollar una analogía eléctrica de un sistema mecánico, hay que describirlo como una red mecánica abstracta. El sistema mecánico se descompone en una serie de elementos ideales, cada uno de los cuales puede asociarse a un análogo eléctrico.^[4]​ Los símbolos utilizados para estos elementos mecánicos en los diagramas de red se muestran en las siguientes secciones sobre cada elemento individual.

Los análogos mecánicos de los elementos eléctricos también son elementos de bulto, es decir, se supone que el componente mecánico que posee el elemento es lo suficientemente pequeño como para que pueda despreciarse el tiempo que tardan las ondas mecánicas en propagarse de un extremo al otro del componente. Las analogías también pueden desarrollarse para elementos distribuidos, como las líneas de transmisión, pero las mayores ventajas se obtienen con los circuitos de elementos fijos. Se necesitan analogías mecánicas para los tres elementos eléctricos pasivos: resistencia, inductancia y capacitancia.^[5]​ En la analogía de la movilidad, el análogo del voltaje es la velocidad y el análogo de la corriente es la fuerza.^[6]​ La impedancia mecánica se define como la relación entre la fuerza y la velocidad, por lo que no es análoga a la impedancia eléctrica. Más bien, es el análogo de la admitancia eléctrica, la inversa de la impedancia. La admitancia mecánica se denomina más comúnmente movilidad,^[7]​ de ahí el nombre de la analogía.^[8]​

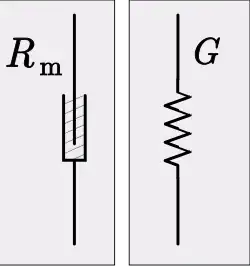
La analogía mecánica de la resistencia eléctrica es la pérdida de energía de un sistema en movimiento a través de procesos como la fricción. Un componente mecánico análogo a una resistencia es un amortiguador y la propiedad análoga a la resistencia inversa (conductancia) es la amortiguación (inversa, porque la impedancia eléctrica es la analogía de la inversa de la impedancia mecánica). Una resistencia se rige por la ecuación constitutiva de la ley de Ohm,

${\displaystyle i=vG}$

La ecuación análoga en el ámbito mecánico es,

${\displaystyle F=uR_{\mathrm {m} }}$

donde,

G = 1/R es conductancia

R es resistencia

v es voltaje

i es corriente

Rm es resistencia mecánica, o amortiguamiento

F es fuerza

u es velocidad inducida por la fuerza.^[11]​

La conductancia eléctrica representa la parte real de la admitancia eléctrica. Del mismo modo, la resistencia mecánica es la parte real de la impedancia mecánica.^[12]​

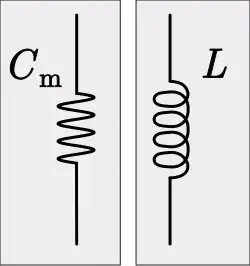
La analogía mecánica de la inductancia en la analogía de la movilidad es la conformidad. En mecánica es más común hablar de rigidez, la inversa de la conformidad. Un componente mecánico análogo a un inductor es un muelle. Un inductor se rige por la ecuación constitutiva,

${\displaystyle v=L{\frac {di}{dt}}}$

La ecuación análoga en el ámbito mecánico es una forma de la ley de Hooke,

${\displaystyle u=C_{\mathrm {m} }{\frac {dF}{dt}}}$

donde,

L es la inductancia

t es el tiempo

Cm = 1/S es la conformidad mecánica

S es la rigidez^[15]​

${\displaystyle Z=j\omega L}$

La admitancia mecánica análoga viene dada por,

${\displaystyle Y_{\mathrm {m} }=j\omega C_{\mathrm {m} }}$

donde,

Z es la impedancia eléctrica

j es la unidad imaginaria

ω es la frecuencia angular

Ym es la admitancia mecánica.^[16]​

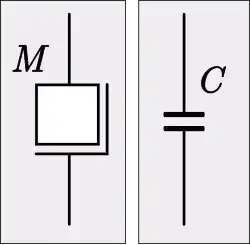
La analogía mecánica de la capacitancia en la analogía de la movilidad es la masa. Un componente mecánico análogo a un condensador es un peso grande y rígido o un Inerter mecánico.

Un condensador se rige por la ecuación constitutiva,

${\displaystyle i=C{\frac {dv}{dt}}}$

La ecuación análoga en el ámbito mecánico es la segunda ley del movimiento de Newton,

${\displaystyle F=M{\frac {du}{dt}}}$

donde,

C es la capacidad

M es la masa

La impedancia de un condensador es puramente imaginaria y viene dada por,

${\displaystyle Z={1 \over j\omega C}}$

La admitancia mecánica análoga viene dada por,

${\displaystyle Y_{\mathrm {m} }={1 \over j\omega M}}$^[18]​

La masa como analogía de un elemento eléctrico plantea una curiosa dificultad. Está relacionada con el hecho de que, en los sistemas mecánicos, la velocidad de la masa (y, lo que es más importante, su aceleración) siempre se mide con respecto a algún sistema de referencia fijo, normalmente la Tierra. Considerada como un elemento de sistema de dos terminales, la masa tiene un terminal a velocidad “'u”', análogo al potencial eléctrico. El otro terminal está a velocidad cero y es análogo al potencial eléctrico de tierra. Por lo tanto, la masa no puede utilizarse como el análogo de un condensador sin conexión a tierra.^[19]​

Esto llevó a Malcolm C. Smith, de la Universidad de Cambridge, a definir en 2002 un nuevo elemento de almacenamiento de energía para redes mecánicas denominado inercia. Un componente que posee inercia se denomina inertizador. Los dos terminales de un inertizador, a diferencia de una masa, pueden tener dos velocidades y aceleraciones diferentes y arbitrarias. La ecuación constitutiva de un inertizador viene dada por,^[20]​

${\displaystyle F=B\left({\frac {du_{\mathrm {2} }}{dt}}-{\frac {du_{\mathrm {1} }}{dt}}\right)=B{\frac {d\Delta u}{dt}}}$

donde,

F es una fuerza igual y opuesta aplicada a los dos terminales

B es la inercia

u1 y u2 son las velocidades en los terminales 1 y 2 respectivamente

Δu = u2 - u1

La inercia tiene las mismas unidades que la masa (kilogramos en el sistema SI) y el nombre indica su relación con la inercia. Smith no se limitó a definir un elemento teórico de la red, sino que también sugirió una construcción para un componente mecánico real y fabricó un pequeño prototipo. El inertizador de Smith consiste en un émbolo capaz de deslizarse dentro o fuera de un cilindro. El émbolo está conectado a un engranaje de piñón y cremallera que acciona un volante de inercia dentro del cilindro. Puede haber dos volantes de inercia contrarrotantes para evitar que se desarrolle un par de torsión. La energía suministrada al empujar el émbolo hacia dentro se devuelve cuando el émbolo se mueve en la dirección opuesta, por lo que el dispositivo almacena energía en lugar de disiparla como un bloque de masa. Sin embargo, la masa real del inerter puede ser muy pequeña, un inerter ideal no tiene masa. Dos puntos del inertizador, el émbolo y la caja del cilindro, pueden conectarse independientemente a otras partes del sistema mecánico sin que ninguno de ellos esté necesariamente conectado a tierra.^[21]​

El inerter de Smith ha encontrado una aplicación en las carreras de Fórmula 1, donde se conoce como J-damper. Se utiliza como alternativa al ahora prohibido amortiguador de masa sintonizada y forma parte de la suspensión del vehículo. Es posible que McLaren lo utilizara por primera vez en secreto en 2005 tras una colaboración con Smith. Ahora se cree que otros equipos lo utilizan. El inerter es mucho más pequeño que el amortiguador de masa sintonizada y suaviza las variaciones de carga de la zona de contacto de los neumáticos.^[22]​ Smith también sugiere utilizar el inerter para reducir las vibraciones de la máquina.^[23]​

La dificultad de la masa en las analogías mecánicas no se limita a la analogía de la movilidad. También se da el mismo problema en la analogía de la impedancia, pero en este caso se trata de inductores sin conexión a tierra, en lugar de condensadores, que no pueden representarse con los elementos estándar.^[24]​

Un resonador mecánico consta de un elemento de masa y un elemento de conformidad. Los resonadores mecánicos son análogos a los circuitos eléctricos LC que consisten en inductancia y capacitancia. Los componentes mecánicos reales tienen inevitablemente masa y conformidad, por lo que resulta práctico fabricar resonadores como un único componente. De hecho, es más difícil fabricar una masa pura o una conformidad pura como componente único. Se puede fabricar un muelle con una cierta elasticidad y minimizar la masa, o una masa con una elasticidad minimizada, pero ninguno de los dos puede eliminarse por completo. Los resonadores mecánicos son un componente clave de los filtros mecánicos.^[25]​

Existen análogos para los elementos eléctricos activos de la fuente de tensión y la fuente de corriente (generadores). El análogo mecánico en la analogía de movilidad del generador de corriente constante es el generador de fuerza constante. El análogo mecánico del generador de tensión constante es el generador de velocidad constante.^[27]​

Un ejemplo de generador de fuerza constante es el muelle de fuerza constante. Un ejemplo práctico de generador de velocidad constante es una máquina potente ligeramente cargada, como un motor, que acciona una correa. Esto es análogo a una fuente de tensión real, como una batería, que permanece casi a tensión constante con carga siempre que la resistencia de carga sea mucho mayor que la resistencia interna de la batería.^[28]​

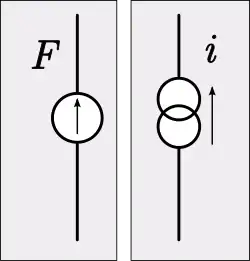
Los sistemas electromecánicos requieren transductores para convertir entre los dominios eléctrico y mecánico. Son análogos a las redes de dos puertos y, como éstas, pueden describirse mediante un par de ecuaciones simultáneas y cuatro parámetros arbitrarios. Existen numerosas representaciones posibles, pero la forma más aplicable a la analogía de la movilidad tiene los parámetros arbitrarios en unidades de admitancia. En forma matricial (con el lado eléctrico tomado como puerto 1) esta representación es,

${\displaystyle {\begin{bmatrix}i\\u\end{bmatrix}}={\begin{bmatrix}y_{11}&y_{12}\\y_{21}&y_{22}\end{bmatrix}}{\begin{bmatrix}v\\F\end{bmatrix}}}$

El elemento 𝑦 22 es la admitancia mecánica de cortocircuito, es decir, la admitancia presentada por el lado mecánico del transductor cuando se aplica tensión cero (cortocircuito) al lado eléctrico. El elemento 𝑦11, por el contrario, es la admitancia eléctrica sin carga, es decir, la admitancia presentada por el lado eléctrico cuando el lado mecánico no está conduciendo una carga (fuerza cero). Los dos elementos restantes, 𝑦21 y 𝑦12, describen las funciones de transferencia directa e inversa del transductor, respectivamente. Ambas son análogas a las admitancias de transferencia y son relaciones híbridas de una magnitud eléctrica y mecánica.^[30]​

La analogía mecánica de un transformador es una máquina simple como una polea o una palanca. La fuerza aplicada a la carga puede ser mayor o menor que la fuerza de entrada dependiendo de si la ventaja mecánica de la máquina es mayor o menor que la unidad respectivamente. La ventaja mecánica es análoga a la inversa de la relación de vueltas del transformador en la analogía de la movilidad. Una ventaja mecánica menor que la unidad es análoga a un transformador elevador y mayor que la unidad es análoga a un transformador reductor.^[31]​

Tabla de ecuaciones análogas de potencia y energía en la analogía de la movilidad

Cantidad eléctrica	Expresión eléctrica	Analogía mecánica	Expresión mecánica
Energía suministrada	${\displaystyle E=\int vi\ dt}$	Energía suministrada	${\displaystyle E=\int Fu\ dt}$
Potencia suministrada	${\displaystyle P=vi}$	Potencia suministrada	${\displaystyle P=Fu}$
Potencia disipada en una resistencia	${\displaystyle P=i^{2}R={v^{2} \over R}}$	Potencia disipada en un amortiguador[11]​	${\displaystyle P=u^{2}R_{\mathrm {m} }={F^{2} \over R_{\mathrm {m} }}}$
Energía almacenada en el campo magnético de un inductor	${\displaystyle E={\tfrac {1}{2}}Li^{2}}$	Energía potencial almacenada en un muelle[1]​	${\displaystyle E={\tfrac {1}{2}}C_{\mathrm {m} }F^{2}}$
Energía almacenada en el campo eléctrico de un condensador	${\displaystyle E={\tfrac {1}{2}}Cv^{2}}$	Energía cinética de una masa en movimiento[1]​	${\displaystyle E={\tfrac {1}{2}}Mu^{2}}$

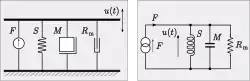
La figura muestra una disposición mecánica de una plataforma de masa M que está suspendida sobre el sustrato por un muelle de rigidez S y un amortiguador de resistencia Rm. El circuito equivalente de analogía de movilidad se muestra a la derecha de esta disposición y consiste en un circuito resonante paralelo. Este sistema tiene una frecuencia de resonancia y puede tener una frecuencia natural de oscilación si no está demasiado amortiguado.^[32]​

La principal ventaja de la analogía de la movilidad sobre su alternativa, la analogía de la impedancia, es que preserva la topología del sistema mecánico. Los elementos que están en serie en el sistema mecánico están en serie en el circuito eléctrico equivalente y los elementos en paralelo en el sistema mecánico permanecen en paralelo en el equivalente eléctrico.^[32]​

El principal inconveniente de la analogía de movilidad es que no mantiene la analogía entre la impedancia eléctrica y la mecánica. La impedancia mecánica se representa como una admitancia eléctrica y una resistencia mecánica se representa como una conductancia eléctrica en el circuito eléctrico equivalente. La fuerza no es análoga a la tensión (las tensiones de los generadores suelen denominarse fuerza electromotriz), sino que es análoga a la corriente.^[22]​

Históricamente, la analogía de la impedancia se utilizó mucho antes que la analogía de la movilidad. La admitancia mecánica y la analogía de la movilidad asociada fueron introducidas por F. A. Firestone en 1932 para superar el problema de la preservación de las topologías.^[33]​W. Hähnle tuvo independientemente la misma idea en Alemania. Horace M. Trent desarrolló un tratamiento para las analogías en general desde la perspectiva de la teoría matemática de grafos e introdujo una nueva analogía propia.^[34]​

1. ↑ ^{a b c} Talbot-Smith, pág. 1.86
2. ↑ Carr, págs. 170–171
3. ↑ Eargle, págs. 5–8
4. ↑ Kleiner, págs. 69–70
5. ↑ Busch-Vishniac, págs. 18–20
6. ↑ Eargle, pág. 5
7. ↑ Fahy & Gardonio, p. 71
8. ↑ Busch-Vishniac, p. 19
9. ↑ Eargle, p. 4
10. ↑ Kleiner, p. 71
11. ↑ ^{a b} Kleiner, p. 71
12. ↑ Atkins & Escudier, p. 216
13. ↑ ^{a b} Eargle, p. 5
14. ↑ Kleiner, p. 73
15. ↑ Smith, p. 1651
16. ↑ Kleiner, pp. 73–74
17. ↑ Kleiner, p. 74
18. ↑ Kleiner, pp. 72–73
19. ↑ Busch-Vishniac, p. 20
20. ↑ Smith, pp. 1649–1650
21. ↑ Smith, pp. 1650–1651
22. ↑ ^{a b} De Groote
23. ↑ Smith, p. 1661
24. ↑ Smith, p. 1649
25. ↑ Taylor & Huang, pp. 377–383
26. ↑ Kleiner, p. 77 Beranek & Mellow, p. 70
27. ↑ Kleiner, pp. 76–77
28. ↑ Kleiner, p. 77
29. ↑ Kleiner, p. 76 Beranek & Mellow, p. 70
30. ↑ Debnath & Roy, pp. 566–567
31. ↑ Kleiner, pp. 74–76 Beranek & Mellow, pp. 76–77
32. ↑ ^{a b} Eargle, pp. 4–5
33. ↑ Pierce, p. 321 Firestone Pusey, p. 547
34. ↑ Findeisen, p. 26 Busch-Vishniac, pp. 19–20 Hähnle Trent

• Atkins, Tony; Escudier, Marcel, A Dictionary of Mechanical Engineering, Oxford University Press, 2013 ISBN 0199587434.
• Beranek, Leo Leroy; Mellow, Tim J., Acoustics: Sound Fields and Transducers, Academic Press, 2012 ISBN 0123914213.
• Busch-Vishniac, Ilene J., Electromechanical Sensors and Actuators, Springer Science & Business Media, 1999 ISBN 038798495X.
• Carr, Joseph J., RF Components and Circuits, Newnes, 2002 ISBN 0-7506-4844-9.
• Debnath, M. C.; Roy, T., "Transfer scattering matrix of non-uniform surface acoustic wave transducers", International Journal of Mathematics and Mathematical Sciences, vol. 10, vol. 3, pp. 563-581, 1987.
• De Groote, Steven, "J-dampers in Formula One", F1 Technical, 27 de septiembre de 2008.
• Eargle, John, Loudspeaker Handbook, Kluwer Academic Publishers, 2003 ISBN 1402075847.
• Fahy, Frank J.; Gardonio, Paolo, Sound and Structural Vibration: Radiation, Transmission and Response, Academic Press, 2007 ISBN 0080471102.
• Findeisen, Dietmar, System Dynamics and Mechanical Vibrations, Springer, 2000 ISBN 3540671447.
• Firestone, Floyd A., "A new analogy between mechanical and electrical systems", Journal of the Acoustical Society of America, vol. 4, pp. 249-267 (1932-1933).
• Hähnle, W., "Die Darstellung elektromechanischer Gebilde durch rein elektrische Schaltbilder", Wissenschaftliche Veröffentlichungen aus dem Siemens-Konzern, vol. 1, vol. 11, pp. 1-23, 1932.
• Kleiner, Mendel, Electroacoustics, CRC Press, 2013 ISBN 1439836183.
• Pierce, Allan D., Acoustics: an Introduction to its Physical Principles and Applications, Acoustical Society of America 1989 ISBN 0883186128.
• Pusey, Henry C. (ed), 50 years of shock and vibration technology, Shock and Vibration Information Analysis Center, Booz-Allen & Hamilton, Inc., 1996 ISBN 0964694026.
• Smith, Malcolm C., [1]"Synthesis of mechanical networks: the inerter", IEEE Transactions on Automatic Control, vol. 47, vol. 10, pp. 1648-1662, octubre de 2002.
• Talbot-Smith, Michael, Audio Engineer's Reference Book, Taylor & Francis, 2013 ISBN 1136119736.
• Taylor, John; Huang, Qiuting, CRC Handbook of Electrical Filters, CRC Press, 1997 ISBN 0849389518.
• Trent, Horace M., "Isomorphisms between oriented linear graphs and lumped physical systems", The Journal of the Acoustical Society of America, vol. 27, pp. 500-527, 1955.