Analogía de impedancia

La analogía de impedancia es un método para representar un sistema mecánico mediante un sistema eléctrico análogo. La ventaja de hacerlo así es que existe un gran cuerpo de teoría y técnicas de análisis sobre sistemas eléctricos complejos, especialmente en el campo de los filtros.^[1]​ Al convertir a una representación eléctrica, estas herramientas del dominio eléctrico pueden aplicarse directamente a un sistema mecánico sin modificaciones. Otra ventaja se da en los sistemas electromecánicos: La conversión de la parte mecánica de un sistema de este tipo al dominio eléctrico permite analizar todo el sistema como un todo unificado.

El comportamiento matemático del sistema eléctrico simulado es idéntico al comportamiento matemático del sistema mecánico representado. A cada elemento del dominio eléctrico le corresponde un elemento del dominio mecánico con una ecuación constitutiva análoga. Todas las leyes del análisis de circuitos, como las leyes de circuitos de Kirchhoff, que se aplican en el dominio eléctrico también se aplican a la analogía de impedancia mecánica.

La analogía de la impedancia es una de las dos principales analogías mecánico-eléctricas utilizadas para representar sistemas mecánicos en el dominio eléctrico; la otra es la analogía de la movilidad. Los papeles de la tensión y la corriente se invierten en estos dos métodos, y las representaciones eléctricas producidas son los circuitos duales de cada uno. La analogía de la impedancia mantiene la analogía entre la impedancia eléctrica y la impedancia mecánica, mientras que la analogía de la movilidad no. Por otra parte, la analogía de la movilidad conserva la topología del sistema mecánico cuando se transfiere al dominio eléctrico, mientras que la analogía de la impedancia no.

La analogía de la impedancia se utiliza mucho para modelar el comportamiento de los filtros mecánicos. Se trata de filtros destinados a ser utilizados en un circuito electrónico, pero que funcionan íntegramente mediante ondas vibratorias mecánicas. A la entrada y a la salida del filtro hay transductores que realizan la conversión entre los dominios eléctrico y mecánico.^[2]​

Otro uso muy común es en el campo de los equipos de audio, como los altavoces. Los altavoces constan de un transductor y piezas mecánicas móviles. Las propias ondas acústicas son ondas de movimiento mecánico: de moléculas de aire o de algún otro medio fluido. Una de las primeras aplicaciones de este tipo fue mejorar notablemente el pésimo rendimiento sonoro de los fonógrafos. En 1929, Edward Norton diseñó los componentes mecánicos de un fonógrafo para que se comportaran como un filtro plano máximo, anticipándose así al filtro electrónico de Butterworth.^[3]​

Antes de poder desarrollar una analogía eléctrica para un sistema mecánico, primero hay que describirlo como una red mecánica abstracta. El sistema mecánico se descompone en una serie de elementos ideales, a cada uno de los cuales se puede asociar un análogo eléctrico.^[4]​ Los símbolos utilizados para estos elementos mecánicos en los diagramas de red se muestran en las siguientes secciones sobre cada elemento individual.

Los análogos mecánicos de los elementos eléctricos también son elementos de bulto, es decir, se supone que el componente mecánico que posee el elemento es lo suficientemente pequeño como para que pueda despreciarse el tiempo que tardan las ondas mecánicas en propagarse de un extremo al otro del componente. Las analogías también pueden desarrollarse para elementos distribuidos, como las líneas de transmisión, pero las mayores ventajas se obtienen con los circuitos de elementos fijos. Se necesitan analogías mecánicas para los tres elementos eléctricos pasivos: resistencia, inductancia y capacitancia. Estas analogías vienen determinadas por la propiedad mecánica elegida para representar el "esfuerzo", la analogía del voltaje, y la propiedad elegida para representar el "flujo", la analogía de la corriente.^[5]​ En la analogía de la impedancia, la variable de esfuerzo es la fuerza y la variable de flujo es la velocidad.^[6]​

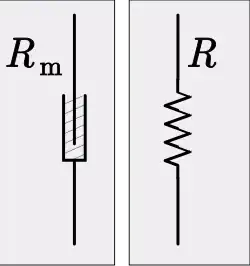
La analogía mecánica de la resistencia eléctrica es la pérdida de energía de un sistema en movimiento a través de procesos como la fricción. Un componente mecánico análogo a una resistencia es un amortiguador y la propiedad análoga a la resistencia es la amortiguación. Una resistencia se rige por la ecuación constitutiva de la ley de Ohm,$${\displaystyle v=iR\,.}$$

La ecuación análoga en el dominio mecánico es, $${\displaystyle F=uR_{\mathrm {m} }\,,}$$

donde 𝑅 es la resistencia;

𝑣 es el voltaje; 𝑖 es la corriente;

𝑅𝑚 es la resistencia mecánica, o amortiguamiento;

𝐹 es la fuerza; y 𝑢es la velocidad inducida por la fuerza.[6]

La resistencia eléctrica representa la parte real de la impedancia eléctrica. Del mismo modo, la resistencia mecánica es la parte real de la impedancia mecánica.^[9]​

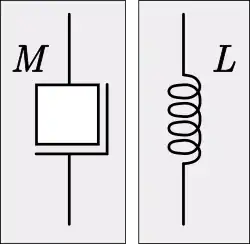
La analogía mecánica de la inductancia en la analogía de la impedancia es la masa. Un componente mecánico análogo a un inductor es un peso grande y rígido. Un inductor se rige por la ecuación constitutiva,$${\displaystyle v=L{\frac {di}{dt}}\,.}$$

La ecuación análoga en el ámbito mecánico es la segunda ley del movimiento de Newton,$${\displaystyle F=M{\frac {du}{dt}}\,,}$$

𝐿 es la inductancia;

𝑡 es el tiempo; y

𝑀 es la masa.[6]

La impedancia de un inductor es puramente imaginaria y viene dada por $${\displaystyle Z=j\omega L\,.}$$

La impedancia mecánica análoga viene dada por,$${\displaystyle Z_{\mathrm {m} }=j\omega M\,,}$$

donde

𝑍es la impedancia eléctrica;

𝑗es la unidad imaginaria;

𝜔es la frecuencia angular; y

𝑍𝑚 es la impedancia mecánica.[10]

La analogía mecánica de la capacitancia en la analogía de la impedancia es la conformidad. En mecánica es más común hablar de rigidez, la inversa de la conformidad. Un componente mecánico análogo a un condensador es un muelle^[12]​ Un condensador se rige por la ecuación constitutiva.^[9]​

$${\displaystyle v=D\int idt\,.}$$

La ecuación análoga en el ámbito mecánico es una forma de la ley de Hooke,

$${\displaystyle F=S\int udt\,,}$$

donde

𝐷=1/𝐶 es la elastancia;

𝐶es la capacitancia; y

𝑆 es la rigidez.

La impedancia de un condensador es puramente imaginaria y viene dada por,$${\displaystyle Z={\frac {D}{j\omega }}\,.}$$La impedancia mecánica análoga viene dada por,

$${\displaystyle Z_{\mathrm {m} }={\frac {S}{j\omega }}\,.}$$

Alternativamente, se puede escribir,

$${\displaystyle Z_{\mathrm {m} }={\frac {1}{j\omega C_{\mathrm {m} }}}\,,}$$

donde 𝐶𝑚=1/𝑆 es la conformidad mecánica. Esto es más directamente análogo a la expresión eléctrica cuando se utiliza la capacitancia.^[13]​

Un resonador mecánico consta tanto de un elemento de masa como de un elemento de conformidad. Los resonadores mecánicos son análogos a los circuitos eléctricos LC que constan de inductancia y capacitancia. Los componentes mecánicos reales tienen inevitablemente masa y conformidad, por lo que resulta práctico fabricar resonadores como un único componente. De hecho, es más difícil fabricar una masa pura o una conformidad pura como componente único. Se puede fabricar un muelle con una cierta elasticidad y minimizar la masa, o una masa con una elasticidad minimizada, pero ninguno de los dos puede eliminarse por completo. Los resonadores mecánicos son un componente clave de los filtros mecánicos.^[14]​

Existen análogos para los elementos eléctricos activos de la fuente de tensión y la fuente de corriente (generadores). El análogo mecánico en la analogía de impedancia del generador de tensión constante es el generador de fuerza constante. El análogo mecánico del generador de corriente constante es el generador de velocidad constante.^[16]​

Un ejemplo de generador de fuerza constante es el muelle de fuerza constante. Es análogo a una fuente de tensión real, como una batería, que se mantiene casi a tensión constante con carga siempre que la resistencia de carga sea mucho mayor que la resistencia interna de la batería. Un ejemplo práctico de generador de velocidad constante es una máquina potente ligeramente cargada, como un motor, que acciona una correa.^[17]​

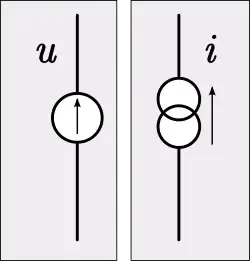
Los sistemas electromecánicos requieren transductores para convertir entre los dominios eléctrico y mecánico. Son análogos a las redes de dos puertos y, como éstas, pueden describirse mediante un par de ecuaciones simultáneas y cuatro parámetros arbitrarios. Existen numerosas representaciones posibles, pero la forma más aplicable a la analogía de la impedancia tiene los parámetros arbitrarios en unidades de impedancia. En forma de matriz (con el lado eléctrico tomado como puerto 1) esta representación es,[$${\displaystyle {\begin{bmatrix}v\\F\end{bmatrix}}={\begin{bmatrix}z_{11}&z_{12}\\z_{21}&z_{22}\end{bmatrix}}{\begin{bmatrix}i\\u\end{bmatrix}}\,.}$$El elemento 𝑧22 es la impedancia mecánica en circuito abierto, es decir, la impedancia que presenta el lado mecánico del transductor cuando no entra corriente (circuito abierto) en el lado eléctrico. El elemento 𝑧11, por el contrario, es la impedancia eléctrica bloqueada, es decir, la impedancia que presenta el lado eléctrico cuando el lado mecánico está bloqueado y no puede moverse (la velocidad es cero). Los dos elementos restantes, 𝑧21 y 𝑧12,

describen las funciones de transferencia directa e inversa del transductor, respectivamente. Ambas son análogas a las impedancias de transferencia y son relaciones híbridas de una magnitud eléctrica y mecánica.^[19]​

La analogía mecánica de un transformador es una máquina simple como una polea o una palanca. La fuerza aplicada a la carga puede ser mayor o menor que la fuerza de entrada dependiendo de si la ventaja mecánica de la máquina es mayor o menor que la unidad respectivamente. La ventaja mecánica es análoga a la relación de vueltas del transformador en la analogía de la impedancia. Una ventaja mecánica mayor que la unidad es análoga a un transformador elevador y menor que la unidad es análoga a un transformador reductor.^[20]​

Cantidad eléctrica	Expresión eléctrica	Analogía mecánica	Expresión mecánica
Energía suministrada	${\textstyle E=\int vi\ dt}$	Energía suministrada	${\textstyle E=\int Fu\ dt}$
Potencia suministrada	${\displaystyle P=vi}$	Potencia suministrada	${\displaystyle P=Fu}$
Potencia disipada en una resistencia	${\displaystyle P=i^{2}R={v^{2} \over R}}$	Potencia disipada en un amortiguador[21]​	${\displaystyle P=u^{2}R_{\mathrm {m} }={F^{2} \over R_{\mathrm {m} }}}$
Energía almacenada en el campo magnético de un inductor	${\displaystyle E={\tfrac {1}{2}}Li^{2}}$	Energía cinética de una masa en movimiento[1]​	${\displaystyle E={\tfrac {1}{2}}Mu^{2}}$
Energía almacenada en el campo eléctrico de un condensador	${\displaystyle E={\tfrac {1}{2}}Cv^{2}}$	Energía cinética de una masa en movimiento[1]​	${\displaystyle E={\tfrac {1}{2}}C_{\mathrm {m} }F^{2}}$

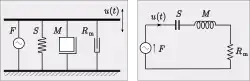
La figura muestra una disposición mecánica de una plataforma de masa 𝑀 que está suspendida por encima del sustrato mediante un muelle de rigidez 𝑆 y un amortiguador de resistencia 𝑅.

El circuito equivalente de analogía de impedancias se muestra a la derecha de esta disposición y consiste en un circuito resonante en serie. Este sistema tiene una frecuencia de resonancia y puede tener una frecuencia natural de oscilación si no está demasiado amortiguado.^[22]​

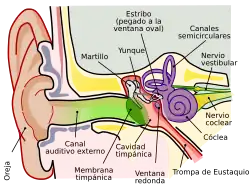
El diagrama del circuito muestra un modelo de analogía de impedancia del oído humano. A la sección del conducto auditivo le sigue un transformador que representa el tímpano. El tímpano es el transductor entre las ondas acústicas en el aire del conducto auditivo y las vibraciones mecánicas en los huesos del oído medio. En la cóclea se produce otro cambio de medio, de las vibraciones mecánicas al fluido que llena la cóclea. Este ejemplo demuestra el poder de las analogías eléctricas para reunir tres dominios (acústico, mecánico y flujo de fluidos) en un todo unificado. Si también se hubieran incluido en el modelo los impulsos nerviosos que fluyen hacia el cerebro, el dominio eléctrico habría hecho que el modelo abarcara cuatro dominios.

La parte del circuito correspondiente a la cóclea utiliza un análisis de elementos finitos de la línea de transmisión continua del conducto coclear. Una representación ideal de una estructura de este tipo utilizaría elementos infinitesimales, por lo que habría un número infinito de ellos. En este modelo, la cóclea se divide en 350 secciones y cada sección se modela utilizando un pequeño número de elementos lumped.^[23]​

La principal ventaja de la analogía de la impedancia sobre su alternativa, la analogía de la movilidad, es que mantiene la analogía entre la impedancia eléctrica y la mecánica. Es decir, una impedancia mecánica se representa como una impedancia eléctrica y una resistencia mecánica se representa como una resistencia eléctrica en el circuito eléctrico equivalente. También es natural pensar en la fuerza como análoga a la tensión (las tensiones de los generadores suelen denominarse fuerza electromotriz) y en la velocidad como análoga a la corriente. Es esta analogía básica la que conduce a la analogía entre la impedancia eléctrica y la mecánica.^[24]​

La principal desventaja de la analogía de la impedancia es que no preserva la topología del sistema mecánico. Los elementos que están en serie en el sistema mecánico están en paralelo en el circuito eléctrico equivalente y viceversa.^[25]​

La representación de la matriz de impedancia de un transductor transforma la fuerza en el dominio mecánico en corriente en el dominio eléctrico. Del mismo modo, la velocidad en el dominio mecánico se transforma en tensión en el dominio eléctrico. Un dispositivo de dos puertos que transforma una tensión en una cantidad análoga puede representarse como un transformador simple. Un dispositivo que transforma una tensión en un análogo de la propiedad dual de la tensión (es decir, la corriente, cuyo análogo es la velocidad) se representa como un girador.^[26]​Dado que la fuerza es análoga a la tensión, no a la corriente, esto puede parecer una desventaja a primera vista. Sin embargo, muchos transductores prácticos, especialmente a frecuencias de audio, funcionan por inducción electromagnética y se rigen por una relación similar.^[27]​ Por ejemplo, la fuerza sobre un conductor que transporta corriente viene dada por

$${\displaystyle F=BIl\,,}$$

,donde 𝐵 es la densidad de flujo magnético; y

𝑙 es la longitud del conductor.

La analogía de la impedancia se denomina a veces analogía de Maxwell^[24]​por James Clerk Maxwell (1831-1879), que utilizó analogías mecánicas para explicar sus ideas sobre los campos electromagnéticos.^[28]​ Sin embargo, el término impedancia no se acuñó hasta 1886 (por Oliver Heaviside),^[29]​la idea de impedancia compleja fue introducida por Arthur E. Kennelly en 1893, y el concepto de impedancia no se extendió al ámbito mecánico hasta 1920 por Kennelly y Arthur Gordon Webster.^[30]​

Henri Poincaré, en 1907, fue el primero en describir un transductor como un par de ecuaciones algebraicas lineales que relacionan variables eléctricas (tensión y corriente) con variables mecánicas (fuerza y velocidad).^[31]​ Wegel, en 1921, fue el primero en expresar estas ecuaciones en términos de impedancia mecánica, además de impedancia eléctrica.^[32]​

1. ↑ ^{a b c} Talbot-Smith, pág. 1.86
2. ↑ Carr, págs. 170–171
3. ↑ Darlington, pág. 7 Harrison
4. ↑ Kleiner, págs. 69–70
5. ↑ Busch-Vishniac, pág. 20
6. ↑ Talbot-Smith, págs. 1.85–1.86
7. ↑ ^{a b c} Eargle, p. 4
8. ↑ Kleiner, p. 71
9. ↑ ^{a b} Kleiner, pág. 71
10. ↑ Kleiner, p. 74
11. ↑ Kleiner, p. 73
12. ↑ Pipes y Harvill, pág. 187
13. ↑ Kleiner, págs. 72–73
14. ↑ Taylor y Huang, págs. 377–383
15. ↑ Kleiner, p. 76 Beranek & Mellow, p. 70
16. ↑ Kleiner, págs. 76–77
17. ↑ Kleiner, pág. 77
18. ↑ Kleiner, p. 77 Beranek & Mellow, p. 70
19. ↑ Jackson, págs. 16-17 Paik, pág. 572
20. ↑ Kleiner, págs. 74–76 Beranek y Mellow, págs. 76–77
21. ↑ Eargle, pág. 4
22. ↑ Eargle, págs. 3–4
23. ↑ Fukazawa y Tanaka, págs. 191-192
24. ↑ ^{a b} Busch-Vishniac, pág. 20
25. ↑ Busch-Vishniac, págs. 20-21 Eargle, págs. 4-5
26. ↑ Beranek y Mellow, págs. 70–71
27. ↑ Eargle, págs. 5–7
28. ↑ Stephens y Bate, pág. 421
29. ↑ Martinsen y Grimnes, pág. 287
30. ↑ Caza pág. 66
31. ↑ Pierce, pág. 200, cita a Poincaré
32. ↑ Hunt, pág. 66 Pierce, pág. 200, cita a Wegel

• • Beranek, Leo Leroy; Mellow, Tim J., Acoustics: Sound Fields and Transducers, Academic Press, 2012 ISBN 0123914213.
  • Busch-Vishniac, Ilene J., Electromechanical Sensors and Actuators, Springer Science & Business Media, 1999 ISBN 038798495X.
  • Carr, Joseph J., RF Components and Circuits, Newnes, 2002 ISBN 0-7506-4844-9.
  • Darlington, S. "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors", IEEE Transactions on Circuits and Systems, vol. 31, no. 1, pp. 3–13, 1984.
  • Eargle, John, Loudspeaker Handbook, Kluwer Academic Publishers, 2003 ISBN 1402075847.
  • Fukazawa, Tatsuya; Tanaka, Yasuo, "Evoked otoacoustic emissions in a cochlear model", pp. 191–196 in Hohmann, D. (ed), ECoG, OAE and Intraoperative Monitoring: Proceedings of the First International Conference, Würzburg, Germany, September 20–24, 1992, Kugler Publications, 1993 ISBN 9062990975.
  • Harrison, Henry C. "Acoustic device", U.S. patent 1,730,425, presentada el 11 de octubre de 1927 (y en Alemania el 21 de octubre de 1923), expedida el 8 de octubre de 1929.
  • Hunt, Frederick V., Electroacoustics: the Analysis of Transduction, and its Historical Background, Harvard University Press, 1954 OCLC 2042530.
  • Jackson, Roger G., Novel Sensors and Sensing, CRC Press, 2004 ISBN 1420033808.
  • Kleiner, Mendel, Electroacoustics, CRC Press, 2013 ISBN 1439836183.
  • Martinsen, Orjan G.; Grimnes, Sverre, Bioimpedance and Bioelectricity Basics, Academic Press, 2011 ISBN 0080568807.
  • Paik, H. J., "Superconduction accelerometers, gravitational-wave transducers, and gravity gradiometers", pp. 569–598, in Weinstock, Harold, SQUID Sensors: Fundamentals, Fabrication, and Applications, Springer Science & Business Media, 1996 ISBN 0792343506.
  • Pierce, Allan D., Acoustics: an Introduction to its Physical Principles and Applications, Acoustical Society of America 1989 ISBN 0883186128.
  • Pipes, Louis A.; Harvill, Lawrence R., Applied Mathematics for Engineers and Physicists, Courier Dover Publications, 2014 ISBN 0486779513.
  • Poincaré, H., "Study of telephonic reception", Eclairage Electrique, vol. 50, pp. 221–372, 1907.
  • Stephens, Raymond William Barrow; Bate, A. E., Acoustics and vibrational physics, Edward Arnold, 1966 OCLC 912579.
  • Talbot-Smith, Michael, Audio Engineer's Reference Book, Taylor & Francis, 2013 ISBN 1136119736.
  • Taylor, John; Huang, Qiuting, CRC Handbook of Electrical Filters, CRC Press, 1997 ISBN 0849389518.
  • Wegel, R. L., "Theory of magneto-mechanical systems as applied to telephone receivers and similar structures", Journal of the American Institute of Electrical Engineers, vol. 40, pp. 791–802, 1921.