Análogos n-dimensionales del cubo de Rubik

Un análogo n-dimensional del cubo de Rubik es un rompecabezas cuya geometría y funcionamiento son análogos a los del cubo de Rubik, pero que está concebido sobre un hipercubo de cualquier número de dimensiones. Estos modelos análogos tienen ${\displaystyle n^{d}}$ piezas diferentes, donde d es el número de dimensiones del hipercubo y n es el número partes en las que se divide cualquiera de las líneas que unen dos vértices del mismo. El conocido cubo de Rubik es un hipercubo con ${\displaystyle 3^{3}}$ = 27 piezas cúbicas, de las cuales una es invisible por estar en el centro del cubo. Dado que la mecánica de un objeto de cuatro dimensiones o más no puede ser representada físicamente, todos estos rompecabezas análogos existen únicamente como programas de ordenador, siendo el más popular el juego "Magic Cube 4d".

Cada uno de los análogos tiene sus piezas cubiertas por pegatinas de colores, que tienen ${\displaystyle d-1}$ dimensiones. Sin embargo, sólo un subconjunto de las piezas muestran sus pegatinas al exterior, es decir, hay piezas con un distinto número de pegatinas visibles en d dimensiones. Por ejemplo, en el cubo de Rubik existen piezas que tienen 0, 1, 2, y 3 pegatinas. En general los análogos de distintas dimensiones contienen ${\displaystyle d+1}$ tipos distintos de piezas. Para cada tipo distinto de piezas se puede conocer el número total de ellas en el rompecabezas a través de la fórmula

${\displaystyle 2^{s}\cdot {}_{d}\,C_{s}}$

donde d es el número de dimensiones, s es el número de pegatinas de un tipo de pieza particular, y ${\displaystyle {}_{d}\,C_{s}}$ es el número de combinaciones de d elementos tomados de s en s, lo que es igual a

${\displaystyle {\frac {d!}{s!(d-s)!}}}$

Si se añade a la fórmula el operador ${\displaystyle n-2}$ se obtiene una expresión para el número de piezas de cualquier n, d y s

${\displaystyle 2^{s}\cdot {}_{d}\,C_{s}\cdot (n-2)}$

A partir de estos planteamientos se puede deducir el número de piezas de todos los tipos. Por ejemplo, para los análogos del tipo ${\displaystyle 3^{d}}$ se tiene que:

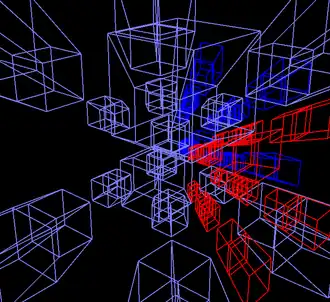
El cubo de Rubik es el original y más conocido de los rompecabezas de combinación tridimensionales. Se han realizado numerosas representaciones virtuales de este rompecabezas mediante programas de ordenador para crear rompecabezas con movimientos secuenciales en más de tres dimensiones. Aunque un rompecabezas de este tipo nunca podría construirse físicamente, las reglas de su funcionamiento están definidas matemáticamente con bastante rigor y son análogas a las reglas de la geometría tridimensional. Por lo tanto, pueden simularse mediante software. Al igual que con los rompecabezas mecánicos de movimientos secuenciales, existen registros de quienes los resuelven, aunque aún no se alcanza el mismo grado de organización competitiva.

• Vértice. Punto de dimensión cero en el que se unen figuras de dimensiones superiores.
• Arista. Figura unidimensional en la que se unen figuras de dimensiones superiores.
• Cara. Figura bidimensional en la que (para objetos de dimensión mayor a tres) se unen figuras de dimensión superior.
• Celda. Figura tridimensional en la que (para objetos de dimensión mayor a cuatro) se unen figuras de dimensión superior.
• n-politopo. Figura n-dimensional que continúa como se indicó anteriormente. El nombre del politopo puede reemplazar al de la forma geométrica específica, como cuando se denomina 4-cubo para referirse al teseracto.
• n-celda. Una figura de dimensión superior que contiene n celdas.
• Pieza. Una sola parte móvil del rompecabezas con la misma dimensión que el rompecabezas completo.
• Cubito. En la comunidad de resolución de problemas, este es el término generalmente usado para denominar a una 'pieza'.
• Pegatina. Las etiquetas de colores en el rompecabezas que identifican el estado del mismo. Por ejemplo, los cubos de las esquinas de un cubo de Rubik son una sola pieza, pero cada uno tiene tres pegatinas de distintos colores. Las pegatinas en rompecabezas de mayor dimensión tendrán una dimensionalidad mayor que dos. Por ejemplo, en el cubo de 4, las pegatinas son sólidos tridimensionales.

A modo de comparación, los datos relativos al cubo de Rubik estándar 3³ son los siguientes:

Número de combinaciones posibles ${\displaystyle ={\frac {12!\cdot 8!}{2}}\cdot {\frac {2^{12}}{2}}\cdot {\frac {3^{8}}{3}}\sim 10^{20}}$

Existe cierto debate sobre si los cubos con el centro de las caras deben contarse como piezas separadas, ya que no se pueden mover entre sí. Es posible que se indique un número diferente de piezas en distintas fuentes. En este artículo, se cuentan los cubos con el centro de las caras, ya que esto hace que las secuencias aritméticas sean más consistentes y, sin duda, se pueden rotar, por lo que su posición interviene en los algoritmos. Sin embargo, el cubo del centro no se cuenta porque no tiene pegatinas visibles y, por lo tanto, no requiere solución. Aritméticamente, se debería tener:

${\displaystyle P=V+E+F+C\,\!}$

Pero a P siempre le falta una unidad (o la extensión n-dimensional de esta fórmula) en las cifras de este artículo, ya que C (o el politopo de mayor dimensión correspondiente, para dimensiones superiores) no se contabiliza.

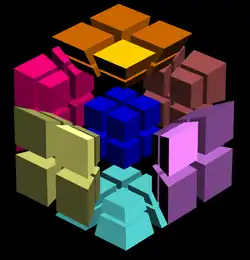
Figura geométrica: Teseracto

El software Superliminal MagicCube4D incluye muchas versiones de politopos 4D con distintas formas de giro, incluyendo cubos N⁴. La interfaz de usuario permite giros y rotaciones 4D, además de controlar parámetros de visualización 4D como la proyección en 3D, el tamaño y espaciado de los cubos y el tamaño de las pegatinas.

Superliminal Software mantiene un Salón de la Fama para quienes baten récords en este rompecabezas.

Combinaciones alcanzables:^[2]​

${\displaystyle ={\frac {24!\cdot 32!}{2}}\cdot {\frac {16!}{2}}\cdot 2^{23}\cdot (3!)^{31}\cdot 3\cdot {\left({\frac {4!}{2}}\right)}^{15}\cdot 4}$

${\displaystyle \sim 10^{120}\,\!}$

Combinaciones alcanzables:^[2]​

${\displaystyle {}={\frac {15!}{2}}\cdot {\left({\frac {4!}{2}}\right)}^{14}\cdot 4}$

${\displaystyle {}\sim 10^{28}\,\!}$

Combinaciones alcanzables:^[2]​

${\displaystyle ={\frac {15!}{2}}\cdot \left({\frac {4!}{2}}\right)^{14}\cdot 4\cdot {\frac {64!}{2}}\cdot 3^{63}\cdot {\frac {96!\cdot 2}{2\cdot (4!)^{24}}}\cdot {\frac {2^{95}\cdot 64!\cdot 2}{2\cdot (8!)^{8}}}}$

${\displaystyle \sim 10^{334}\,\!}$

Combinaciones alcanzables:^[2]​

${\displaystyle ={\frac {48!}{(6!)^{8}}}\cdot {\frac {96!}{(12!)^{8}}}\cdot {\frac {64!}{(8!)^{8}}}\cdot {\frac {24!\cdot 32!}{2}}\cdot (3!)^{31}\cdot 2^{23}\cdot {\frac {64!}{2}}\cdot }$${\displaystyle 3^{63}\cdot 16!\cdot \left({\frac {4!}{2}}\right)^{15}\cdot 4\cdot {\frac {96!}{(4!)^{24}}}\cdot 2^{95}\cdot {\frac {96!}{(4!)^{24}}}\cdot 2^{95}}$

${\displaystyle \sim 10^{701}\,\!}$

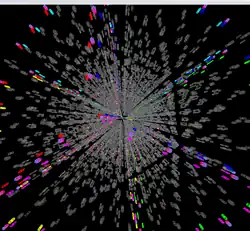
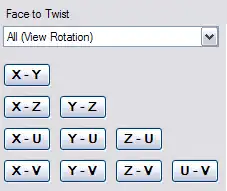
Forma geométrica: Penteracto

El Cubo Mágico 5D de Roice Nelson permite renderizar rompecabezas de 5 cubos en seis tamaños, desde 2⁵ hasta 7⁵. Permite giros 5D y controles para rotar el cubo en múltiples dimensiones, controles de perspectiva 4D y 5D, y controles de espaciado y tamaño de cubos y pegatinas, similares a los de Magiccube4D.

Sin embargo, un rompecabezas 5D es mucho más difícil de comprender que uno 4D. Una característica esencial de la implementación de Roice es la posibilidad de desactivar o resaltar los cubos y pegatinas seleccionados. Aun así, la complejidad de las imágenes generadas sigue siendo considerable, como se puede apreciar en las capturas de pantalla.

Roice mantiene un Salón de la Locura para quienes baten récords en este rompecabezas. Hasta el 6 de enero de 2011, se habían encontrado dos soluciones exitosas para el cubo de 5 de tamaño 7⁵.^[3]​

Combinaciones posibles:^[4]​

${\displaystyle ={\frac {32!}{2}}\cdot 60^{32}\cdot {\frac {80!}{2}}\cdot {\frac {24^{80}}{2}}\cdot {\frac {40!\cdot 80!}{2}}\cdot {\frac {6^{80}}{2}}\cdot {\frac {2^{40}}{2}}}$

${\displaystyle \sim 10^{561}\,\!}$

Combinaciones alcanzables:^[4]​

${\displaystyle ={\frac {31!}{2}}\cdot 60^{31}}$

${\displaystyle \sim 10^{89}\,\!}$

Combinaciones alcanzables:^[4]​

${\displaystyle ={\frac {31!}{2}}\cdot 60^{31}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {160!}{16!^{10}}}}$

${\displaystyle \sim 10^{2075}\,\!}$

Combinaciones alcanzables:^[4]​

${\displaystyle {\begin{matrix}={\frac {32!}{2}}\cdot 60^{32}\cdot {\frac {80!}{2}}\cdot {\frac {24^{80}}{2}}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {40!\cdot 80!}{2}}\cdot {\frac {6^{80}}{2}}\cdot {\frac {2^{40}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {240!}{(6!)^{40}}}\cdot {\frac {2^{240}}{2}}\cdot {\frac {320!}{(8!)^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {480!}{(12!)^{40}}}\cdot {\frac {2^{480}}{2}}\cdot {\frac {80!}{(8!)^{10}}}\cdot {\frac {160!}{(16!)^{10}}}\cdot \\{\frac {240!}{(24!)^{10}}}\cdot {\frac {320!}{(32!)^{10}}}\end{matrix}}}$

${\displaystyle \sim 10^{5267}\,\!}$

Combinaciones alcanzables:^[4]​

${\displaystyle {\begin{matrix}={\frac {31!}{2}}\cdot 60^{31}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {640!}{24^{160}}}\cdot {\frac {3^{640}}{3}}\cdot {\frac {320!}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {320!}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot \\{\frac {640!}{64!^{10}}}\cdot {\frac {160!}{16!^{10}}}\cdot {\frac {160!}{16!^{10}}}\end{matrix}}}$

${\displaystyle \sim 10^{11441}\,\!}$

Combinaciones alcanzables:^[4]​

${\displaystyle {\begin{matrix}={\frac {32!}{2}}\cdot 60^{32}\cdot {\frac {80!}{2}}\cdot {\frac {24^{80}}{2}}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {160!}{2}}\cdot {\frac {12^{160}}{3}}\cdot {\frac {80!\cdot 40!}{2}}\cdot {\frac {6^{80}}{2}}\cdot {\frac {2^{40}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {640!}{24^{160}}}\cdot {\frac {3^{640}}{3}}\cdot {\frac {320!}{24^{80}}}\cdot {\frac {6^{320}}{2}}\cdot {\frac {240!}{6!^{40}}}\cdot \\{\frac {2^{240}}{2}}\cdot {\frac {480!}{12!^{40}}}\cdot {\frac {2^{480}}{2}}\cdot {\frac {320!}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {240!}{6!^{40}}}\cdot {\frac {2^{240}}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {480!}{12!^{40}}}\cdot {\frac {2^{480}}{2}}\cdot {\frac {960!}{24!^{40}}}\cdot {\frac {2^{960}}{2}}\cdot {\frac {320!}{8!^{40}}}\cdot {\frac {2^{320}}{2}}\cdot {\frac {80!}{8!^{10}}}\cdot {\frac {240!}{24!^{10}}}\cdot {\frac {320!}{32!^{10}}}\cdot {\frac {160!}{16!^{10}}}\cdot {\frac {80!}{8!^{10}}}\cdot \\{\frac {480!}{48!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {240!}{24!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {960!}{96!^{10}}}\cdot {\frac {320!}{32!^{10}}}\cdot {\frac {640!}{64!^{10}}}\cdot {\frac {160!}{16!^{10}}}\end{matrix}}}$

${\displaystyle \sim 10^{21503}\,\!}$

Figura geométrica: Hexeracto (6D) y Hepteracto (7D)

El software del Cubo Mágico 7D de Andrey Astrelin es capaz de generar rompecabezas de hasta 7 dimensiones en doce tamaños, desde 3⁴ hasta 5⁷.

A julio de 2024, en cuanto a los rompecabezas exclusivos del Cubo Mágico 7D, solo se habían resuelto los rompecabezas 3⁶, 3⁷, 4⁶ y 5⁶.^[5]​

Figura geométrica: 120-celdas (también llamado hecatonicosacoron o dodecacontacoron)

El cubo de 120 celdas es una figura geométrica 4D (polícoro) compuesta por 120 dodecahedra, que a su vez es una figura 3D compuesta por 12 pentágono. El rompecabezas de 120 celdas es el análogo en 4 dimensiones del dodecaedro, de la misma manera que el teseracto (4 cubos) es el análogo en 4 dimensiones del cubo. El rompecabezas de movimiento secuencial de 120 celdas de Gravitation3d es, por lo tanto, el análogo en 4 dimensiones del rompecabezas 3D Megaminx, que tiene la forma de un dodecaedro.

El rompecabezas está representado en un solo tamaño (tres cubos por lado) y en seis esquemas de color de diferente dificultad. El rompecabezas completo requiere un color diferente para cada celda (120 colores). Esta gran cantidad de colores aumenta la dificultad del rompecabezas, ya que algunos tonos son bastante difíciles de distinguir. La forma más sencilla es con dos toros entrelazados, cada uno formando un anillo de cubos de diferentes dimensiones. La lista completa de esquemas de color es la siguiente:

• Toros de 2 colores.

• Celdas de 4 cubos de 9 colores. Es decir, el mismo esquema de colores que el cubo de 4.
• Capas de 9 colores.
• Anillos de 12 colores.
• Antípoda de 60 colores. Cada par de celdas dodecaédricas diametralmente opuestas es del mismo color.
• Rompecabezas completo de 120 colores.

Los controles son muy similares a los del Cubo Mágico 4D, con ajustes para la perspectiva 4D, el tamaño de la celda, el tamaño y la distancia de la pegatina, y el zoom y la rotación habituales. Además, se pueden desactivar completamente los grupos de celdas según la selección de toros, celdas del cubo de 4, capas o anillos.

Gravitation3d ha creado un "Salón de la Fama" para quienes lo resuelvan, quienes deben proporcionar un archivo de registro de su solución. Hasta abril de 2017, el rompecabezas se había resuelto doce veces.^[6]​

Combinaciones alcanzables:^[7]​

${\displaystyle ={\frac {600!}{2}}\cdot {\frac {1200!}{2}}\cdot {\frac {720!}{2}}\cdot {\frac {2^{720}}{2}}\cdot {\frac {6^{1200}}{2}}\cdot {\frac {12^{600}}{3}}}$

${\displaystyle \sim 10^{8126}\,}$

Este cálculo de combinaciones alcanzables no se ha demostrado matemáticamente y solo puede considerarse un límite superior. Su deducción supone la existencia del conjunto de algoritmos necesarios para crear todas las combinaciones de "cambio mínimo". No hay razón para suponer que estos algoritmos no se encontrarán, ya que quienes resuelven rompecabezas los han logrado en todos los rompecabezas similares resueltos hasta la fecha.

Figura geométrica: Cuadrado

Un rompecabezas tipo Rubik en 2D no se puede construir físicamente, al igual que uno en 4D.^[8]​ Un rompecabezas en 3D podría construirse sin pegatinas en la tercera dimensión, lo que se comportaría como un rompecabezas en 2D, pero su verdadera materialización permanece en el mundo virtual. La imagen que se muestra aquí es de Superliminal, que lo denomina Cubo Mágico 2D.

Este rompecabezas no resulta de gran interés para quienes lo resuelven, ya que su solución es bastante trivial. Esto se debe, en gran parte, a que no es posible colocar una pieza en su posición con un giro. Algunos de los algoritmos más difíciles del cubo de Rubik estándar consisten en lidiar con estos giros, donde una pieza está en su posición correcta, pero no en la orientación correcta. En rompecabezas de dimensiones superiores, este giro puede adoptar la forma, bastante desconcertante, de una pieza aparentemente al revés. Basta con comparar la dificultad del rompecabezas 2×2×2 con la del 3×3 (que tiene el mismo número de piezas) para ver que esta capacidad de causar giros en dimensiones superiores tiene mucho que ver con la dificultad, y por consiguiente con la satisfacción al resolver el siempre popular cubo de Rubik.

Combinaciones posibles:

${\displaystyle =4!\,\!=24}$

Las piezas centrales tienen una orientación fija entre sí (igual que las piezas centrales del cubo estándar de 3×3×3) y, por lo tanto, no se tienen en cuenta en el cálculo de combinaciones.

Este rompecabezas no es un análogo bidimensional del cubo de Rubik. Si el grupo de operaciones sobre un solo politopo de un rompecabezas de n dimensiones se define como cualquier rotación de un politopo de (n–1) dimensiones en un espacio de (n–1) dimensiones, entonces el tamaño del grupo,

• Para el cubo de 5, las rotaciones de un politopo de 4 dimensiones en el espacio de 4 dimensiones son 8×6×4 = 192
• Para el cubo de 4 dimensiones son las rotaciones de un politopo de 3 dimensiones (cubo) en el espacio de 3 dimensiones = 6×4 = 24
• Para el cubo de 3 dimensiones son las rotaciones de un politopo de 2 dimensiones (cuadrado) en el espacio de 2 dimensiones = 4
• Para el cubo de 2 dimensiones son las rotaciones de un politopo de 1 dimensiones en el espacio de 1 dimensiones = 1

En otras palabras, el rompecabezas de 2 dimensiones no se puede resolver a la vez. Todo esto si se aplican las mismas restricciones a los movimientos que en el rompecabezas 3D real. Los movimientos asignados al Cubo Mágico 2D son operaciones de reflexión. Esta operación de reflexión puede extenderse a rompecabezas de dimensiones superiores. Para el cubo 3D, la operación análoga sería retirar una cara y reemplazarla con las pegatinas orientadas hacia el cubo. Para el cubo de 4 dimensiones, la operación análoga sería retirar un cubo y volver a colocarlo al revés.

Otro rompecabezas de dimensiones alternativas es una vista que se puede lograr en el Cubo Mágico 3D de David Vanderschel. Un cubo de 4 dimensiones proyectado en una pantalla de computadora 2D es un ejemplo general de un rompecabezas de n dimensiones proyectado en un espacio de (n–2) dimensiones. La analogía 3D de esta disposición es proyectar el cubo en una representación unidimensional, que es lo que el programa de Vanderschel es capaz de hacer.

Vanderschel lamenta que nadie haya afirmado haber resuelto la proyección 1D de este rompecabezas.^[9]​ Sin embargo, dado que no se conservan registros de este rompecabezas, podría no ser cierto que esté sin resolver.

• Rompecabezas de combinación
• Grupo del cubo de Rubik, estructura algebraica vinculada al cubo.
• Cubo de Rubik
• Dominó de Rubik (3×3×2)

• H. J. Kamack y T. R. Keane, «El Teseracto de Rubik», disponible en línea aquí y archivado el 25 de diciembre de 2008.
• Velleman, D., «El Teseracto de Rubik», «Mathematics Magazine», «Vol. 65», n.º 1 (febrero de 1992), págs. 27–36, Mathematical Association of America. *Pickover, C, «Surfing Through Hyperspace», págs. 120-122, Oxford University Press, 1999.
• Pickover, C, «Alien IQ Test», capítulo 24, Dover Publications, 2001.
• Pickover, C, «The Zen of Magic Squares, Circles, and Stars», págs. 130-133, Princeton University Press, 2001.
• David Singmaster, «Computer Cubists», junio de 2001. Una lista mantenida por Singmaster, que incluye referencias 4D. Consultado el 19 de junio de 2008.

• Superliminal
• Anatomía de un cubo de Rubik de dimensión d de Gravitation3d
• Cubo mágico 3D de David Vanderschel