Algoritmo de Karger

En ciencias de la computación y teoría de grafos, el algoritmo de Karger es un procedimiento probabilista para calcular un corte mínimo de un grafo conexo. Fue ideado por David Karger y publicado por primera vez en 1993.^[1]​

La idea del algoritmo se basa en el concepto de contracción de una arista ${\displaystyle (u,v)}$ en un grafo no dirigido ${\displaystyle G=(V,E)}$. Informalmente, la contracción de una arista fusiona los nodos ${\displaystyle u}$ y ${\displaystyle v}$ en uno, reduciendo el número total de nodos del grafo en uno. Todas las demás aristas que conectan ${\displaystyle u}$ o ${\displaystyle v}$ se reunirán al nodo fusionado, produciendo efectivamente un multigrafo. El algoritmo básico de Karger contrae iterativamente aristas elegidas aleatoriamente hasta que solo quedan dos nodos. Estos nodos representan un corte en el grafo original. Al iterar este algoritmo básico un número suficiente de veces, se puede encontrar un corte mínimo con alta probabilidad.

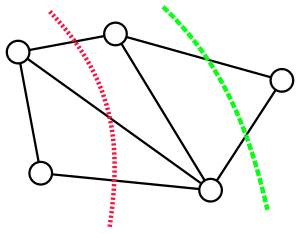
Un corte ${\displaystyle (S,T)}$ en un grafo no dirigido ${\displaystyle G=(V,E)}$ es una partición de los vértices ${\displaystyle V}$ en dos conjuntos no vacíos y disjuntos ${\displaystyle S\cup T=V}$. El conjunto de cortes de un corte consiste en las aristas ${\displaystyle \{\,uv\in E\colon u\in S,v\in T\,\}}$ entre las dos partes. El tamaño (o peso) de un corte en un grafo no ponderado es la cardinalidad del conjunto de cortes, es decir, el número de aristas entre las dos partes.

${\displaystyle w(S,T)=|\{\,uv\in E\colon u\in S,v\in T\,\}|\,.}$

Existen ${\displaystyle 2^{|V|}}$ maneras para determinar si cada vértice pertenece a ${\displaystyle S}$ o a ${\displaystyle T}$, pero dos de estas opciones hacen que ${\displaystyle S}$ o ${\displaystyle T}$ sean intersecciones vacías y no generan cortes. Entre las opciones restantes, intercambiar los roles de ${\displaystyle S}$ y ${\displaystyle T}$ no altera el corte, por lo que cada corte se cuenta dos veces; por lo tanto, hay ${\displaystyle 2^{|V|-1}-1}$ cortes distintos. El problema del corte mínimo consiste en encontrar el corte de menor tamaño entre estos cortes.

Para grafos ponderados con pesos de arista positivos ${\displaystyle w\colon E\rightarrow \mathbf {R} ^{+}}$, el peso del corte es la suma de los pesos de las aristas entre los vértices de cada parte

${\displaystyle w(S,T)=\sum _{uv\in E\colon u\in S,v\in T}w(uv)\,,}$

lo que concuerda con la definición no ponderada de ${\displaystyle w=1}$.

Un corte a veces se denomina corte global para distinguirlo de un corte ${\displaystyle s}$-${\displaystyle t}$ para un par de vértices dado, que tiene el requisito adicional de que ${\displaystyle s\in S}$ y ${\displaystyle t\in T}$. Todo corte global es un corte ${\displaystyle s}$-${\displaystyle t}$ para algún ${\displaystyle s,t\in V}$. Por lo tanto, el problema del corte mínimo se puede resolver en tiempo polinómico iterando sobre todas las opciones de ${\displaystyle s,t\in V}$ y resolviendo el problema de corte mínimo resultante ${\displaystyle s}$-${\displaystyle t}$ utilizando el teorema de flujo máximo y corte mínimo y un algoritmo de tiempo polinómico para el flujo máximo, como el algoritmo de inserción y reetiquetado, aunque este enfoque no es óptimo. Entre los mejores algoritmos deterministas para el problema de corte mínimo global se encuentra el algoritmo de Stoer-Wagner, cuyo tiempo de ejecución es ${\displaystyle O(mn+n^{2}\log n)}$.^[2]​

La operación fundamental del algoritmo de Karger es una variante de la contracción de aristas. El resultado de contraer la arista ${\displaystyle e=\{u,v\}}$ es un nuevo nodo ${\displaystyle uv}$. Cada arista ${\displaystyle \{w,u\}}$ o ${\displaystyle \{w,v\}}$ para ${\displaystyle w\notin \{u,v\}}$ hasta los extremos de la arista contraída se reemplaza por una arista ${\displaystyle \{w,uv\}}$ hasta el nuevo nodo. Finalmente, se eliminan los nodos contraídos ${\displaystyle u}$ y ${\displaystyle v}$ con todas sus aristas incidentes. En particular, el grafo resultante no contiene bucles propios. El resultado de contraer la arista ${\displaystyle e}$ se denota como ${\displaystyle G/e}$.

El algoritmo de contracción contrae repetidamente aristas aleatorias en el grafo hasta que solo quedan dos nodos, momento en el cual solo hay un corte.

La idea clave del algoritmo es que es mucho más probable que las aristas que no son de corte mínimo se seleccionen aleatoriamente y se pierdan por contracción, ya que las aristas con corte mínimo suelen ser ampliamente superadas en número por las aristas que no son de corte mínimo. Posteriormente, es plausible que las aristas con corte mínimo sobrevivan a toda la contracción de aristas, y el algoritmo identificará correctamente la arista con corte mínimo.

   procedimiento contraer(${\displaystyle G=(V,E)}$):
   mientras ${\displaystyle |V|>2}$
        elegir ${\displaystyle e\in E}$ uniformemente al azar
        ${\displaystyle G\leftarrow G/e}$
   devolver el único corte en ${\displaystyle G}$

Cuando el grafo se representa utilizando una lista de adyacencia o una matriz de adyacencia, se puede utilizar una sola operación de contracción de aristas con un número lineal de actualizaciones a la estructura de datos, para un tiempo de ejecución total de ${\displaystyle O(|V|^{2})}$. Alternativamente, el procedimiento puede considerarse como una ejecución del algoritmo de Kruskal para construir el árbol recubridor mínimo en un grafo donde las aristas tienen pesos ${\displaystyle w(e_{i})=\pi (i)}$ según una permutación aleatoria ${\displaystyle \pi }$. Eliminar la arista más pesada de este árbol da como resultado dos componentes que describen un corte. De esta manera, el procedimiento de contracción se puede disponer como el algoritmo de Kruskal en el tiempo ${\displaystyle O(|E|\log |E|)}$.

Los desarrollos más conocidos utilizan ${\displaystyle O(|E|)}$ tiempo y espacio de memoria, o ${\displaystyle O(|E|\log |E|)}$ tiempo y ${\displaystyle O(|V|)}$ espacio, respectivamente.^[1]​

En un grafo ${\displaystyle G=(V,E)}$ con ${\displaystyle n=|V|}$ vértices, el algoritmo de contracción devuelve un corte mínimo con una probabilidad polinómicomente pequeña, ${\displaystyle {\binom {n}{2}}^{-1}}$. Debe recordarse que todo grafo tiene ${\displaystyle 2^{n-1}-1}$ cortes (según lo explicado en la sección anterior), entre los cuales ${\displaystyle {\tbinom {n}{2}}}$ pueden ser, como máximo, cortes mínimos. Por lo tanto, la probabilidad de éxito de este algoritmo es mucho mejor que la probabilidad de elegir un corte al azar, que es, como máximo, ${\displaystyle {\frac {\tbinom {n}{2}}{2^{n-1}-1}}}$.

Por ejemplo, un grafo ciclo con ${\displaystyle n}$ vértices tiene exactamente ${\displaystyle {\binom {n}{2}}}$ cortes mínimos, dados por cada elección de 2 aristas. El procedimiento de contracción encuentra cada uno de estos con la misma probabilidad.

Para establecer con mayor precisión el límite inferior de la probabilidad de éxito, sea ${\displaystyle C}$ el conjunto de las aristas con un corte mínimo específico de tamaño ${\displaystyle k}$. El algoritmo de contracción devuelve ${\displaystyle C}$ si ninguna de las aristas aleatorias eliminadas por el algoritmo pertenece al conjunto de cortes ${\displaystyle C}$. En particular, la primera contracción de arista evita ${\displaystyle C}$, lo que ocurre con una probabilidad de ${\displaystyle 1-k/|E|}$. El grado mínimo de ${\displaystyle G}$ es al menos ${\displaystyle k}$ (de lo contrario, un vértice de grado mínimo induciría un corte más pequeño donde una de las dos particiones contiene solo el vértice de grado mínimo), por lo que ${\displaystyle |E|\geqslant nk/2}$. Por lo tanto, la probabilidad de que el algoritmo de contracción elija una arista de ${\displaystyle C}$ es:

${\displaystyle {\frac {k}{|E|}}\leqslant {\frac {k}{nk/2}}={\frac {2}{n}}.}$

La probabilidad ${\displaystyle p_{n}}$ de que el algoritmo de contracción en un grafo de ${\displaystyle n}$-vértices evite ${\displaystyle C}$ satisface la recurrencia ${\displaystyle p_{n}\geqslant \left(1-{\frac {2}{n}}\right)p_{n-1}}$, con ${\displaystyle p_{2}=1}$, que puede expandirse como:

${\displaystyle p_{n}\geqslant \prod _{i=0}^{n-3}{\Bigl (}1-{\frac {2}{n-i}}{\Bigr )}=\prod _{i=0}^{n-3}{\frac {n-i-2}{n-i}}={\frac {n-2}{n}}\cdot {\frac {n-3}{n-1}}\cdot {\frac {n-4}{n-2}}\cdots {\frac {3}{5}}\cdot {\frac {2}{4}}\cdot {\frac {1}{3}}={\binom {n}{2}}^{-1}\,.}$

Al repetir el algoritmo de contracción ${\displaystyle T={\binom {n}{2}}\ln n}$ veces con elecciones aleatorias independientes y obtener el corte más pequeño, la probabilidad de no encontrar un corte mínimo es:

${\displaystyle \left[1-{\binom {n}{2}}^{-1}\right]^{T}\leq {\frac {1}{e^{\ln n}}}={\frac {1}{n}}\,.}$

El tiempo total de ejecución para ${\displaystyle T}$ repeticiones para un grafo con ${\displaystyle n}$ vértices y ${\displaystyle m}$ aristas es ${\displaystyle O(Tm)=O(n^{2}m\log n)}$.

Una extensión del algoritmo de Karger, debida a David Karger y a Clifford Stein, logra una mejora de un orden de magnitud.^[3]​

La idea básica es realizar el procedimiento de contracción hasta que el grafo alcance ${\displaystyle t}$ vértices.

   procedimiento contrato(${\displaystyle G=(V,E)}$, ${\displaystyle t}$):
   mientras ${\displaystyle |V|>t}$
       elegir ${\displaystyle e\in E}$ uniformemente al azar
       ${\displaystyle G\leftarrow G/e}$
   devolver ${\displaystyle G}$

La probabilidad ${\displaystyle p_{n,t}}$ de que este procedimiento de contracción evite un corte específico ${\displaystyle C}$ en un grafo de ${\displaystyle n}$-vértices es:

${\displaystyle p_{n,t}\geq \prod _{i=0}^{n-t-1}{\Bigl (}1-{\frac {2}{n-i}}{\Bigr )}={\binom {t}{2}}{\Bigg /}{\binom {n}{2}}\,.}$

Esta expresión es aproximadamente ${\displaystyle t^{2}/n^{2}}$ y se vuelve menor que ${\displaystyle {\frac {1}{2}}}$ alrededor de ${\displaystyle t=n/{\sqrt {2}}}$. En particular, la probabilidad de que una arista de ${\displaystyle C}$ se contraiga aumenta hacia el final. Esto motiva la idea de cambiar a un algoritmo más lento después de un cierto número de pasos de contracción.

   procedimiento fastmincut(${\displaystyle G=(V,E)}$):
   si ${\displaystyle |V|\leq 6}$:
       devolver contrato(${\displaystyle G}$, ${\displaystyle 2}$)
   de lo contrario:
       ${\displaystyle t\leftarrow \lceil 1+|V|/{\sqrt {2}}\rceil }$
       ${\displaystyle G_{1}\leftarrow }$ contrato(${\displaystyle G}$, ${\displaystyle t}$)
       ${\displaystyle G_{2}\leftarrow }$ contrato(${\displaystyle G}$, ${\displaystyle t}$)
       devolver minfastmincut(${\displaystyle G_{1}}$), fastmincut(${\displaystyle G_{2}}$)

El parámetro de contracción ${\displaystyle t}$ se elige de modo que cada llamada a la contracción tenga una probabilidad de al menos la mitad de éxito (es decir, de evitar la contracción de una arista de un conjunto de corte específico ${\displaystyle C}$). Esto permite modelar la parte exitosa del árbol de recursión como un árbol binario aleatorio generado por un proceso de Galton-Watson crítico, y analizarlo en consecuencia.^[3]​

La probabilidad ${\displaystyle P(n)}$ de que este árbol aleatorio de llamadas exitosas contenga una ruta lo suficientemente larga como para llegar a la base de la recursión y encontrar ${\displaystyle C}$ viene dada por la relación de recurrencia

${\displaystyle P(n)=1-\left(1-{\frac {1}{2}}P\left({\Bigl \lceil }1+{\frac {n}{\sqrt {2}}}{\Bigr \rceil }\right)\right)^{2}}$

con solución ${\displaystyle P(n)=\Omega \left({\frac {1}{\log n}}\right)}$. El tiempo de ejecución del corte rápido mínimo satisface que

${\displaystyle T(n)=2T\left({\Bigl \lceil }1+{\frac {n}{\sqrt {2}}}{\Bigr \rceil }\right)+O(n^{2})}$

con solución ${\displaystyle T(n)=O(n^{2}\log n)}$. Para alcanzar la probabilidad de error ${\displaystyle O(1/n)}$, el algoritmo puede repetirse ${\displaystyle O(\log n/P(n))}$ veces, para un tiempo de ejecución total de ${\displaystyle T(n)\cdot {\frac {\log n}{P(n)}}=O(n^{2}\log ^{3}n)}$. Esto supone una mejora de un orden de magnitud con respecto al algoritmo original de Karger.^[3]​

Para determinar un corte mínimo, se debe tocar cada arista del grafo al menos una vez, lo que equivale a un tiempo ${\displaystyle \Theta (n^{2})}$ en un grafo denso. El algoritmo de corte mínimo de Karger-Stein requiere un tiempo de ejecución de ${\displaystyle O(n^{2}\ln ^{O(1)}n)}$, que es muy cercano a este.