Ángulos suplementarios

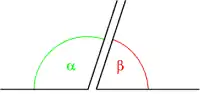
Dos ángulos son ángulos suplementarios por defecto ^[1]​ o, simplemente, ángulos suplementarios, si suman ${\displaystyle 180^{\circ }}$.

Así, se denomina a un ángulo "suplemento" de otro, si aquel es lo que le falta a este para medir un ángulo plano o llano.

Para obtener el ángulo suplementario ${\displaystyle \beta }$ de un determinado ángulo ${\displaystyle \alpha }$, se restará ${\displaystyle \alpha }$ a ${\displaystyle 180^{\circ }}$, de manera que:

${\displaystyle \beta =180^{\circ }-\alpha }$

• Los ángulos que midan más que ${\displaystyle 180^{\circ }}$ no tienen ángulo suplementario.^{[cita requerida]}

• El valor de ${\displaystyle 180^{\circ }}$ es el mismo que dos ángulos rectos, ${\displaystyle \pi }$ rad, ${\displaystyle \tau /2}$ rad o ${\displaystyle 200^{g}}$ grados centesimales.
• Si dos ángulos son suplementarios de otros dos ángulos congruentes, también son congruentes entre sí.
• Los senos de los ángulos suplementarios son los mismos, por ejemplo:

${\displaystyle \operatorname {sen} \alpha =\operatorname {sen}(180^{\circ }-\alpha )}$

${\displaystyle \operatorname {sen} \alpha =\operatorname {sen}(\pi -\alpha )}$

${\displaystyle \operatorname {sen} 120^{\circ }=\operatorname {sen} 60^{\circ }}$

• Los cosenos de los ángulos suplementarios son de igual valor absoluto, pero de signo inverso, como muestran los siguientes ejemplos:

${\displaystyle \cos \alpha =-\cos(180^{\circ }-\alpha )}$

${\displaystyle \cos \alpha =-\cos(\pi -\alpha )}$

${\displaystyle \cos 120^{\circ }=-\cos 60^{\circ }}$

Relaciones aritméticas entre ángulos:

• Ángulos congruentes
• Ángulos complementarios
• Ángulos explementarios
• Ángulos suplementarios por exceso

Relaciones posicionales entre ángulos:

• Ángulos adyacentes
• Ángulos consecutivos
• Ángulos opuestos por el vértice
• Ángulos interiores y exteriores

Determinados por dos paralelas y una transversal:

• Ángulos correspondientes
• Ángulos alternos ^[2]​ ^[3]​ externos e internos
• Ángulos conjugados ^[2]​ ^[3]​ externos e internos

• Wikimedia Commons alberga una categoría multimedia sobre Ángulos suplementarios.