Álgebra de Hopf

En matemáticas, un álgebra de Hopf, llamada así en honor al matemático alemán Heinz Hopf, es una estructura algebraica que combina las propiedades de un álgebra asociativa con unidad y una coálgebra coasociativa con counidad, de manera compatible. Esta combinación da lugar a una biálgebra, que además incorpora un antihomomorfismo denominado antípoda, el cual cumple una identidad específica. Gracias a la existencia de una multiplicación, unidad, comultiplicación, counidad y antípoda compatibles, la teoría de representaciones de un álgebra de Hopf permite construir representaciones tensoriales, triviales y duales de forma natural.

Las álgebras de Hopf surgen de manera natural en diversas áreas de las matemáticas, especialmente en la topología algebraica (donde se originaron, en relación con los H-espacios), así como en la teoría de esquemas de grupo, las álgebras de grupos y otros contextos algebraicos. Se consideran el tipo más familiar de biálgebra. Además, se investigan tanto por sus ejemplos concretos como por sus problemas de clasificación. También tienen aplicaciones significativas en la física matemática, como en la física del estado sólido, la teoría cuántica de campos y la teoría de cuerdas.^[1]​^[2]​^[3]​

Un álgebra de Hopf es una biálgebra (asociativa y coasociativa) ${\displaystyle H}$ sobre un cuerpo ${\displaystyle K}$, equipada con una aplicación ${\displaystyle K}$-lineal ${\displaystyle S:H\to H}$ (denominada antípoda) que cumple el siguiente diagrama conmutativo:

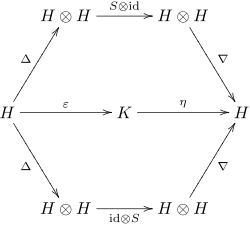
Aquí, ∇ representa la multiplicación, η la unidad, Δ la comultiplicación y ε la counidad de ${\displaystyle H}$.^[4]​ En la notación de Sweedler, la propiedad fundamental se expresa como:

${\displaystyle S(h_{(1)})\,h_{(2)}=h_{(1)}\,S(h_{(2)})=\varepsilon (h)\,1\qquad {\text{para todo }}h\in H.}$

La definición es autodual: si ${\displaystyle H}$ es de dimensión finita, su espacio dual también admite una estructura natural de álgebra de Hopf.^[5]​

Ejemplo	Estructura subyacente	Coproducto	Counidad	Antípoda	¿Conmutativa?	¿Coconmutativa?	Observaciones
Álgebra de grupo ${\displaystyle KG}$	Grupo ${\displaystyle G}$	${\displaystyle \Delta (g)=g\otimes g}$	${\displaystyle \varepsilon (g)=1}$	${\displaystyle S(g)=g^{-1}}$	Sí ⇔ ${\displaystyle G}$ abeliano	Sí
Álgebra de funciones ${\displaystyle K^{G}}$	Grupo finito ${\displaystyle G}$	${\displaystyle \Delta (f)(x,y)=f(xy)}$	${\displaystyle \varepsilon (f)=f(e)}$	${\displaystyle S(f)(x)=f(x^{-1})}$	Sí	Sí ⇔ ${\displaystyle G}$ abeliano	Isomorfo al dual de ${\displaystyle KG}$. Operaciones punto a punto.
Álgebra tensorial ${\displaystyle T(V)}$	Espacio vectorial ${\displaystyle V}$	${\displaystyle \Delta (v)=v\otimes 1+1\otimes v}$	${\displaystyle \varepsilon (v)=0}$	${\displaystyle S(v)=-v}$	Solo si ${\displaystyle \dim V\leq 1}$	Sí	Extendible a las álgebras simétrica y exterior.
Álgebra envolvente universal ${\displaystyle U({\mathfrak {g}})}$	Álgebra de Lie ${\displaystyle {\mathfrak {g}}}$	${\displaystyle \Delta (x)=x\otimes 1+1\otimes x}$	${\displaystyle \varepsilon (x)=0}$	${\displaystyle S(x)=-x}$	Sí ⇔ ${\displaystyle {\mathfrak {g}}}$ abeliana	Sí
Álgebra de Sweedler ${\displaystyle H_{4}}$	Cuerpo ${\displaystyle K}$ de característica distinta de 2	${\displaystyle \Delta (c)=c\otimes c}$, ${\displaystyle \Delta (x)=c\otimes x+x\otimes 1}$	${\displaystyle \varepsilon (c)=1}$, ${\displaystyle \varepsilon (x)=0}$	${\displaystyle S(c)=c}$, ${\displaystyle S(x)=-cx}$	No	No	Álgebra de dimensión 4. Primer ejemplo no conmutativo ni coconmutativo.

• Álgebra asociativa
• Coálgebra
• Biálgebra
• Categoría monoidal

• Dăscălescu, N., Năstăsescu, C. & Raianu, Ș. (2001). *Hopf Algebras. An Introduction*. Marcel Dekker.
• Underwood, R. G. (2011). *An Introduction to Hopf Algebras*. Springer.
• Montgomery, S. (1993). *Hopf Algebras and Their Actions on Rings*. AMS.