Arcotangente
En trigonometría, la arcotangente se define como la función inversa de la tangente de un ángulo. Simbolizada:
| Función arcotangente | ||
|---|---|---|
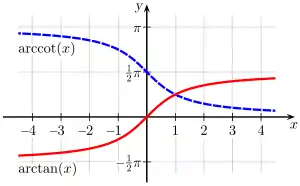 Gráfica de Función arcotangente | ||
| Definición |
| |
| Tipo | Trigonométrica inversa | |
| Dominio | ||
| Codominio | ||
| Imagen | ||
| Cálculo infinitesimal | ||
| Derivada | ||
| Función inversa | ||
| Límites |
| |
| Funciones relacionadas |
arcocoseno arcoseno | |
su significado geométrico es el arco (en radianes) cuya tangente es .
La función tangente no es biyectiva, por lo que no tiene función inversa definida en todo su dominio. Es posible aplicarle una restricción del dominio de modo que se vuelva inyectiva y sobreyectiva. Por convenio es preferible restringir el dominio de la función tangente al intervalo abierto .
Notación
La notación matemática de la arcotangente es arctan; es común la escritura ambigua tan-1. En diversos lenguajes de programación se suelen utilizar las formas ATN, ATAN, ARCTAN, ARCTG y ATG.
Propiedades
Es una función continua y derivable, de clase (es decir, existen sus derivadas de todos los órdenes).
Es una función impar, o sea que .
Algunos valores especiales
Límites en infinito
Derivadas y crecimiento
En particular, resulta ser una función estrictamente creciente.
, que es positivo en y negativo en .
Integral indefinida
Utilizando el método de integración por partes puede calcularse una función primitiva de :
Serie de Maclaurin
Aplicaciones
En un triángulo rectángulo, la arcotangente equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre su cateto opuesto y su cateto adyacente.
Véase también
Enlaces externos
- Weisstein, Eric W. «Arcotangente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Arcocotangente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.